2.2.2 函数的表示法 课件(共23张PPT) 2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 2.2.2 函数的表示法 课件(共23张PPT) 2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 877.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
2.2.2 函数的表示法
1. 通过实例理解函数的三种表示方法及其特点.
2. 理解分段函数的意义,并能简单应用.
3. 能根据函数解析式画出对应的函数图象.
问题1 你还初得记中所学的函数的概念吗?并举例说明已经学过的函数.
我们已经接触过的函数的三种表示法:解析法、列表法和图象法.
将变量的函数关系用代数式表示,是函数表示方法的解析法;
用表格给出变量之间的函数对应关系,是函数表示方法的列表法;
用图形给出变量之间的函数对应关系,是函数表示方法的图象法.
复习回顾
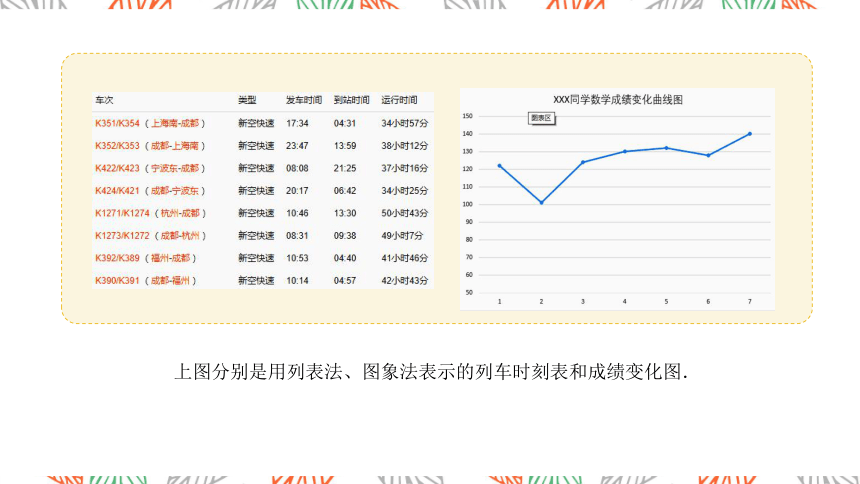
上图分别是用列表法、图象法表示的列车时刻表和成绩变化图.
根据绝对值的定义,分类讨论;
当x<0时,f(x)=|x|=-x;
当x≥0时,f(x)=|x|=x.
探究:画出函数f(x)=|x|的图象.
1
x
y
-1
O
1
思考1: f(x)=|x|不属于之前学过的任何一类函数,
你能将解析式变形,化为不含绝对值的形式吗?
思考2:如何画f(x)=|x|的图象?
f(x)=|x|的图象就是这两部分图象的组合.
在同一直角坐标系中分别画出y=-x,x<0和y=x,x≥0;
其图象为第一、二象限的角平分线,如图所示.
f(x)=|x|=;
思考3:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是否为函数图象的依据是什么?
任意垂直x轴的直线与图象至多有一个交点.
分段函数的特点:在它的定义域中,对于自变量x的不同取值范围,对应关系不同.
像f(x)=,这样的函数称为分段函数.
1
x
y
-1
O
1
讨论:你能举出生活中可以用分段函数描述的实际问题吗?
如出租车的计费、天然气的计费、银行的利率等.
试一试 设x是任一实数,[x]表示不超过x的最大整数,如[-3.14]=-4、[-1]=-1、[3.14]=3、[0.14]=0等,我们把函数y=[x]叫作取整函数(高斯函数);试画出取整函数y=[x]的局部图象.
根据题意,函数y=[x]的定义域为R,值域为Z;
函数的解析式为y=[x]=;
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
O
x
y
-2
-3
-4
-5
-1
函数的图象如右图所示:
对比发现:比较函数的三种表示法,它们各自的特点是什么?
函数表示方法 优点 缺点
解析法
列表法
图像法
①简明、全面地概括了变量间的关系
②通过解析式可以求出任意一个自变量所
对应的函数值
不够直观形象
不需要计算就可以直接看出与自变量相对
应的函数值
只适用于自变量数目少的函数
直观形象反映变化趋势
不精确
思考:所有函数都能用解析法表示吗?列表法与图象法呢?请你举出实例加以说明.
不是所有的函数都能用这三种方法表示,有的函数只能采取某一种表示法;
比如心电图,不能用解析法和列表法表示;
再比如课本第54页给出的狄利克雷函数,不能用图象法表示.
1.下列图象中不能表示函数的图象的是( )
D
A.
B.
C.
D.
x
x
x
x
y
y
y
y
练一练
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(1)在同一直角坐标系中分别画出函数f(x)与g(x)的图象;
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
解答:(1)在同一直角坐标系中画出函数f(x)与g(x)的图象(图1);
图1
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
(2)由图1中函数取值的情况,结合函数M(x)的定义,可得函数M(x)的图象(图2),
图2
由(x+1)2=x+1,得x(x+1)=0,解得x=-1或x=0,
图2
结合图2,得出函数M(x)的解析式为
M(x)=.
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
追问1:如图,你能说说f(x)>g(x)对应图象上有什么特征吗?
当自变量x的取值相同时,函数f(x)对应的点
比函数g(x)对应的点高.
追问2:你能从图象上观察并得出M(x)的取值情况吗?
当x<-1时,g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,此时M(x)=(x+1)2;
当-1<x<0时,f(x)=x+1的图象位于g(x)=(x+1)2的上方,
f(x)=x+1为较大者,此时M(x)=x+1;
当x>0时,g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,此时M(x)=(x+1)2;
当x= 1或x=0时,g(x)=(x+1)2与f(x)=x+1的图象相交,
f(x)与g(x)相等,此时M(x)=f(x)=g(x).
追问3:你能用代数方法求出M(x)的表达式吗?
令f(x)>g(x),即x+1>(x+1)2,
令g(x)>f(x),即(x+1)2>x+1,
令f(x)=g(x),即x+1=(x+1)2,
解得 1<x<0;
解得x< 1或x>0;
解得x= 1或x=0.
综上可得:M(x)=.
A.16
B.18
所以f(5)=f(10)=f(15)=15+3=18.
1.设f(x)=,则f(5)的值为( )
C.21
D.24
B
解析:因为f(x)=,
练一练
A.{-2}
B.
2.已知函数f(x)=,若f(x0)=5,则x0的取值集合是( )
C.{-2,2}
D.
A
与x0>0相矛盾,故舍去;
解得x0=-2,x0=2 (舍去);
若x0>0,可得-2x0=5,可得x0= ,
综上可得:x0=-2.
解析:若x0≤0,可得+1=5,
练一练
1.把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示为x的函数.
解答: y=,x∈(0,50).
2.画出函数y=|x 2|的图象.
解答:图象如图.
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2) x∈R,用m(x)表示f(x)与g(x)中的较小者,记为m(x)=min{f(x),g(x)},请分别用图象法和解析法表示函数m(x).
3.给定函数f(x)= x+1,g(x)=(x 1)2,x∈R.
解答:(1)函数f(x)与g(x)的图象如图1,
图1
图2
(2)由图1得出函数m(x)的图象如图2,
由图2得到函数m(x)的解析式
m(x)=.
(1)函数常用的表示法有哪些?它们各自的特点是什么?
(2)结合本节课的学习,你对如何学习函数又有什么体会?
根据下列问题,回顾本节课所学知识:
(1)解析法、表格法和图象法,
其中解析式是精确的,图象是直观的,表格是直接的.
(2)解析式、表格、图象是对应关系f的不同的表现形式,但实质相同,
为了更好地分析和解决问题,有时需要进行不同表示法的转化和综合使用.
2.2.2 函数的表示法
1. 通过实例理解函数的三种表示方法及其特点.
2. 理解分段函数的意义,并能简单应用.
3. 能根据函数解析式画出对应的函数图象.
问题1 你还初得记中所学的函数的概念吗?并举例说明已经学过的函数.
我们已经接触过的函数的三种表示法:解析法、列表法和图象法.
将变量的函数关系用代数式表示,是函数表示方法的解析法;
用表格给出变量之间的函数对应关系,是函数表示方法的列表法;
用图形给出变量之间的函数对应关系,是函数表示方法的图象法.
复习回顾
上图分别是用列表法、图象法表示的列车时刻表和成绩变化图.
根据绝对值的定义,分类讨论;
当x<0时,f(x)=|x|=-x;
当x≥0时,f(x)=|x|=x.
探究:画出函数f(x)=|x|的图象.
1
x
y
-1
O
1
思考1: f(x)=|x|不属于之前学过的任何一类函数,
你能将解析式变形,化为不含绝对值的形式吗?
思考2:如何画f(x)=|x|的图象?
f(x)=|x|的图象就是这两部分图象的组合.
在同一直角坐标系中分别画出y=-x,x<0和y=x,x≥0;
其图象为第一、二象限的角平分线,如图所示.
f(x)=|x|=;
思考3:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是否为函数图象的依据是什么?
任意垂直x轴的直线与图象至多有一个交点.
分段函数的特点:在它的定义域中,对于自变量x的不同取值范围,对应关系不同.
像f(x)=,这样的函数称为分段函数.
1
x
y
-1
O
1
讨论:你能举出生活中可以用分段函数描述的实际问题吗?
如出租车的计费、天然气的计费、银行的利率等.
试一试 设x是任一实数,[x]表示不超过x的最大整数,如[-3.14]=-4、[-1]=-1、[3.14]=3、[0.14]=0等,我们把函数y=[x]叫作取整函数(高斯函数);试画出取整函数y=[x]的局部图象.
根据题意,函数y=[x]的定义域为R,值域为Z;
函数的解析式为y=[x]=;
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
O
x
y
-2
-3
-4
-5
-1
函数的图象如右图所示:
对比发现:比较函数的三种表示法,它们各自的特点是什么?
函数表示方法 优点 缺点
解析法
列表法
图像法
①简明、全面地概括了变量间的关系
②通过解析式可以求出任意一个自变量所
对应的函数值
不够直观形象
不需要计算就可以直接看出与自变量相对
应的函数值
只适用于自变量数目少的函数
直观形象反映变化趋势
不精确
思考:所有函数都能用解析法表示吗?列表法与图象法呢?请你举出实例加以说明.
不是所有的函数都能用这三种方法表示,有的函数只能采取某一种表示法;
比如心电图,不能用解析法和列表法表示;
再比如课本第54页给出的狄利克雷函数,不能用图象法表示.
1.下列图象中不能表示函数的图象的是( )
D
A.
B.
C.
D.
x
x
x
x
y
y
y
y
练一练
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(1)在同一直角坐标系中分别画出函数f(x)与g(x)的图象;
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
解答:(1)在同一直角坐标系中画出函数f(x)与g(x)的图象(图1);
图1
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
(2)由图1中函数取值的情况,结合函数M(x)的定义,可得函数M(x)的图象(图2),
图2
由(x+1)2=x+1,得x(x+1)=0,解得x=-1或x=0,
图2
结合图2,得出函数M(x)的解析式为
M(x)=.
2.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.
(2) x∈R,用M(x)表示f(x)与g(x)中的较大者,记为M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
追问1:如图,你能说说f(x)>g(x)对应图象上有什么特征吗?
当自变量x的取值相同时,函数f(x)对应的点
比函数g(x)对应的点高.
追问2:你能从图象上观察并得出M(x)的取值情况吗?
当x<-1时,g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,此时M(x)=(x+1)2;
当-1<x<0时,f(x)=x+1的图象位于g(x)=(x+1)2的上方,
f(x)=x+1为较大者,此时M(x)=x+1;
当x>0时,g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,此时M(x)=(x+1)2;
当x= 1或x=0时,g(x)=(x+1)2与f(x)=x+1的图象相交,
f(x)与g(x)相等,此时M(x)=f(x)=g(x).
追问3:你能用代数方法求出M(x)的表达式吗?
令f(x)>g(x),即x+1>(x+1)2,
令g(x)>f(x),即(x+1)2>x+1,
令f(x)=g(x),即x+1=(x+1)2,
解得 1<x<0;
解得x< 1或x>0;
解得x= 1或x=0.
综上可得:M(x)=.
A.16
B.18
所以f(5)=f(10)=f(15)=15+3=18.
1.设f(x)=,则f(5)的值为( )
C.21
D.24
B
解析:因为f(x)=,
练一练
A.{-2}
B.
2.已知函数f(x)=,若f(x0)=5,则x0的取值集合是( )
C.{-2,2}
D.
A
与x0>0相矛盾,故舍去;
解得x0=-2,x0=2 (舍去);
若x0>0,可得-2x0=5,可得x0= ,
综上可得:x0=-2.
解析:若x0≤0,可得+1=5,
练一练
1.把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示为x的函数.
解答: y=,x∈(0,50).
2.画出函数y=|x 2|的图象.
解答:图象如图.
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2) x∈R,用m(x)表示f(x)与g(x)中的较小者,记为m(x)=min{f(x),g(x)},请分别用图象法和解析法表示函数m(x).
3.给定函数f(x)= x+1,g(x)=(x 1)2,x∈R.
解答:(1)函数f(x)与g(x)的图象如图1,
图1
图2
(2)由图1得出函数m(x)的图象如图2,
由图2得到函数m(x)的解析式
m(x)=.
(1)函数常用的表示法有哪些?它们各自的特点是什么?
(2)结合本节课的学习,你对如何学习函数又有什么体会?
根据下列问题,回顾本节课所学知识:
(1)解析法、表格法和图象法,
其中解析式是精确的,图象是直观的,表格是直接的.
(2)解析式、表格、图象是对应关系f的不同的表现形式,但实质相同,
为了更好地分析和解决问题,有时需要进行不同表示法的转化和综合使用.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
