2.1.2 两条直线平行和垂直的判定 课件 (共16张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.1.2 两条直线平行和垂直的判定 课件 (共16张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:35:11 | ||
图片预览




文档简介
(共16张PPT)
2.1.2 两条直线平行和垂直的判定
1.掌握两直线平行或垂直时,直线斜率所满足的关系式;
2.根据斜率判断直线之间的位置关系,判断图形的形状.
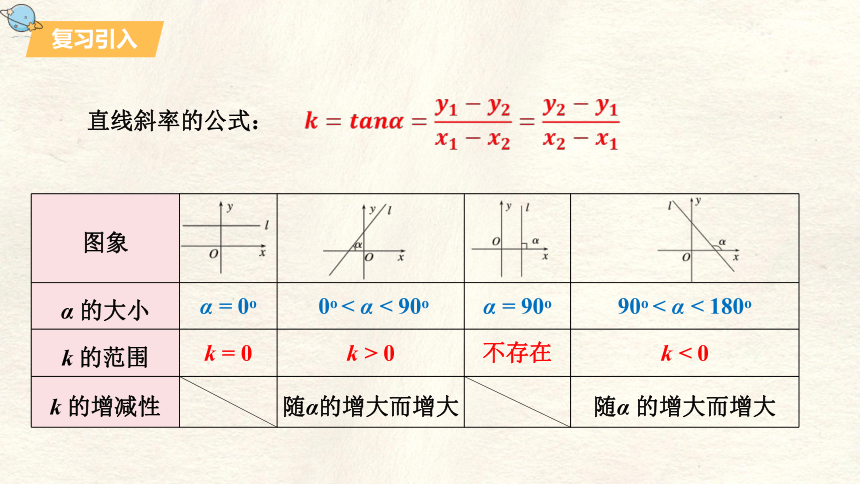
直线斜率的公式:
图象
α 的大小 α = 0o 0o < α < 90o α = 90o 90o < α < 180o
k 的范围 k = 0 k > 0 不存在 k < 0
k 的增减性 随α的增大而增大 随α 的增大而增大
问题 平面中,两条直线的位置关系有哪些?
下面我们一起来探究在坐标中,两条直线特殊的位置关系:
垂直、平行.
若没有特别说明,说“两条直线l1 , l2”时,指两条不重合的直线.
平行和相交
x
o
y
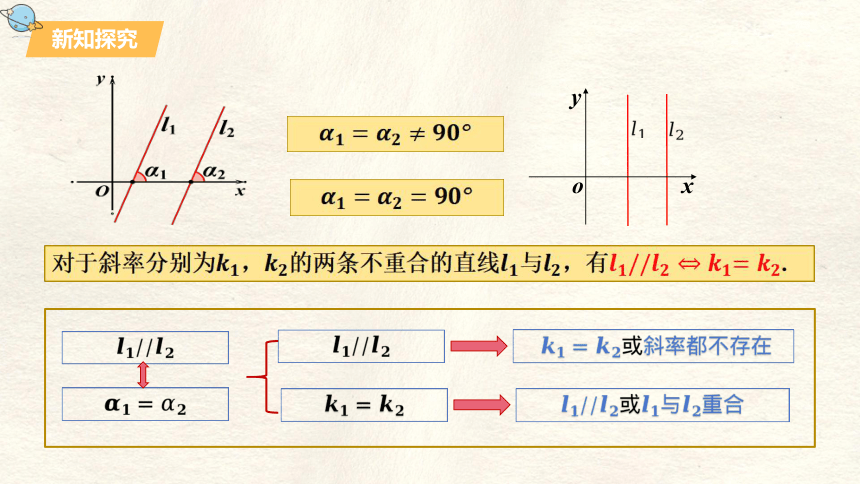
当两条直线与直线平行时,其倾斜角分别为与,斜率分别为与, 与之间有什么关系? 与之间有什么关系?
思考1
x
o
y
对于斜率分别为,的两条不重合的直线与,有.
两种情况:斜率都存在、有一条直线斜率不存在
当直线与直线垂直时,它们的斜率与之间有什么关系?
(1)斜率都存在:设两条直线,的斜率分别为,,则直线,的方向向量分别是,
于是,
即.
(2)一条直线的斜率不存在:
不妨设直线的斜率不存在,即的倾斜角为90°,若 ,则的倾斜角为0°,即.
思考2
1.判断下列各对直线是否平行或垂直:
(1)直线 的斜率为1,经过点;
(2)直线 的倾斜角为30°,经过点;
(3)l1过点M(1,1),N(1,2),l2过点P(1,5),Q(3,5).
解:(1)由题意,;
因此,即.
(2)由题意, ;
因此,即.
(3)由题意不存在,;
所以.
例2.已知,试判断直线AB与PQ的位置关系,并证明你的结论.
解:如图,由已知可得
直线AB的斜率,
直线PQ的斜率,
因为,所以直线AB//PQ.
例3.已知四边形ABCD的四个顶点分别为, ,
,试判断四边形ABCD的形状,并给出证明.
解:如图,由已知可得
AB边所在直线的斜率,
CD边所在直线的斜率,
BC边所在直线的斜率,
DA边所在直线的斜率.
因为, ,
所以AB//CD,BC//DA.
因此四边形ABCD是平行四边形.
o
–1
1
2
3
4
5
6
7
–2
–1
1
2
3
4
5
6
7
–2
x
y
A
D
C
B
2. 已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直 C.可能重合 D.无法确定
B
解 由方程3x2+mx-3=0,
知Δ=m2-4×3×(-3)=m2+36>0恒成立.
故方程有两相异实根,即l1与l2的斜率k1,k2均存在;
设两根为x1,x2,则k1k2=x1x2=-1,所以l1⊥l2.
3.已知直线经过点,直线经过点.
(1)若,求a的值;
(2)若,求a的值.
直线的位置与斜率的关系
2.1.2 两条直线平行和垂直的判定
1.掌握两直线平行或垂直时,直线斜率所满足的关系式;
2.根据斜率判断直线之间的位置关系,判断图形的形状.
直线斜率的公式:
图象
α 的大小 α = 0o 0o < α < 90o α = 90o 90o < α < 180o
k 的范围 k = 0 k > 0 不存在 k < 0
k 的增减性 随α的增大而增大 随α 的增大而增大
问题 平面中,两条直线的位置关系有哪些?
下面我们一起来探究在坐标中,两条直线特殊的位置关系:
垂直、平行.
若没有特别说明,说“两条直线l1 , l2”时,指两条不重合的直线.
平行和相交
x
o
y
当两条直线与直线平行时,其倾斜角分别为与,斜率分别为与, 与之间有什么关系? 与之间有什么关系?
思考1
x
o
y
对于斜率分别为,的两条不重合的直线与,有.
两种情况:斜率都存在、有一条直线斜率不存在
当直线与直线垂直时,它们的斜率与之间有什么关系?
(1)斜率都存在:设两条直线,的斜率分别为,,则直线,的方向向量分别是,
于是,
即.
(2)一条直线的斜率不存在:
不妨设直线的斜率不存在,即的倾斜角为90°,若 ,则的倾斜角为0°,即.
思考2
1.判断下列各对直线是否平行或垂直:
(1)直线 的斜率为1,经过点;
(2)直线 的倾斜角为30°,经过点;
(3)l1过点M(1,1),N(1,2),l2过点P(1,5),Q(3,5).
解:(1)由题意,;
因此,即.
(2)由题意, ;
因此,即.
(3)由题意不存在,;
所以.
例2.已知,试判断直线AB与PQ的位置关系,并证明你的结论.
解:如图,由已知可得
直线AB的斜率,
直线PQ的斜率,
因为,所以直线AB//PQ.
例3.已知四边形ABCD的四个顶点分别为, ,
,试判断四边形ABCD的形状,并给出证明.
解:如图,由已知可得
AB边所在直线的斜率,
CD边所在直线的斜率,
BC边所在直线的斜率,
DA边所在直线的斜率.
因为, ,
所以AB//CD,BC//DA.
因此四边形ABCD是平行四边形.
o
–1
1
2
3
4
5
6
7
–2
–1
1
2
3
4
5
6
7
–2
x
y
A
D
C
B
2. 已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直 C.可能重合 D.无法确定
B
解 由方程3x2+mx-3=0,
知Δ=m2-4×3×(-3)=m2+36>0恒成立.
故方程有两相异实根,即l1与l2的斜率k1,k2均存在;
设两根为x1,x2,则k1k2=x1x2=-1,所以l1⊥l2.
3.已知直线经过点,直线经过点.
(1)若,求a的值;
(2)若,求a的值.
直线的位置与斜率的关系
