2.2.3 直线的一般式方程 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.3 直线的一般式方程 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
2.2.3 直线的一般式方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系;
2.能正确地进行直线的一般式方程与特殊形式的方程的转化;
3.能运用直线的一般式方程解决有关问题.
形式 方程 适用条件
点斜式 斜率存在的直线
斜截式 斜率存在的直线
两点式 斜率存在且不为
截距式 斜率存在且不为,不过原点
直线的方程
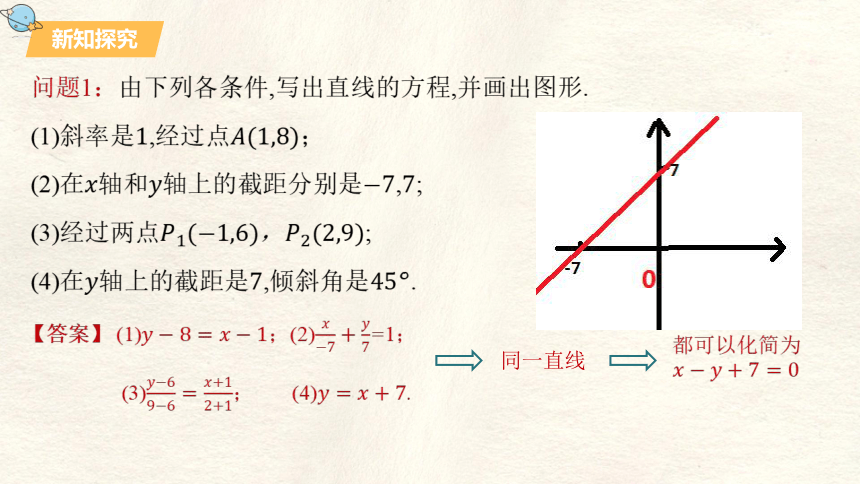
问题1:由下列各条件,写出直线的方程,并画出图形.
(1)斜率是,经过点;
(2)在轴和轴上的截距分别是,;
(3)经过两点,;
(4)在轴上的截距是,倾斜角是.
【答案】 (1);(2)=1;
(3); (4).
同一直线
都可以化简为
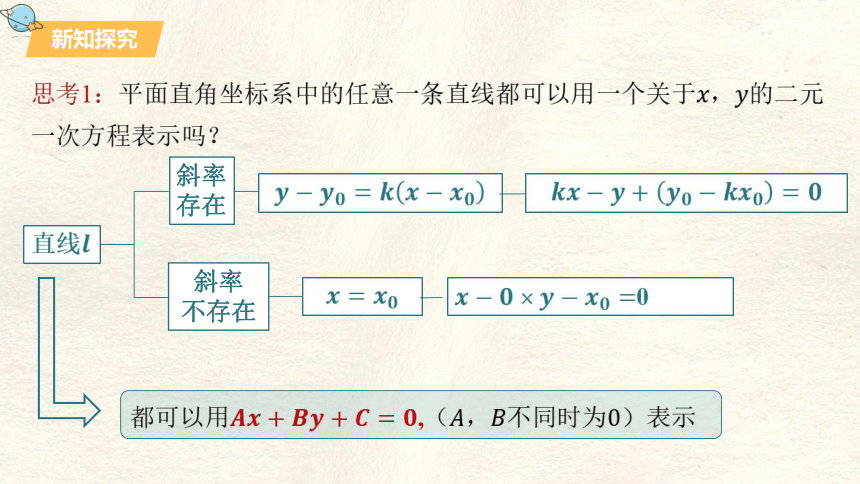
思考1:平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗?
直线
斜率存在
斜率
不存在
0
都可以用,(,不同时为)表示
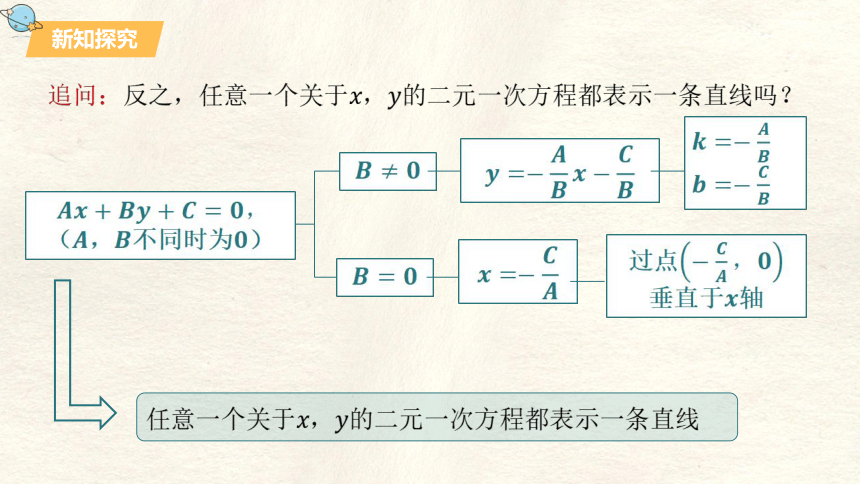
追问:反之,任意一个关于的二元一次方程都表示一条直线吗?
(,不同时为)
过点
垂直于轴
任意一个关于的二元一次方程都表示一条直线
我们把关于的二元一次方程
(其中,不同时为0)叫做直线的一般式方程,简称一般式.
注:①当时,方程可化为,则 是斜率, 是y轴上的截距;
②当时,方程可化为,表示过点,且垂直于x轴的直线.
一般式方程的结构特征:
①要满足A 、B不能同时为0;
②一般式结构特点:左边“x,y,常数依次排列”,右边为“0”;
③可以表示任意直线;
④A>0,A 、B 、C一般是非分式.
1. 斜率为,且在轴上截距为的直线的一般式方程是( )
. .
. .
2. 在直角坐标系中,直线的倾斜角是( )
. . . .
C
C
3.判断正误(正确的打“√”,错误的打“×”)
(1)直线的一般式方程可以表示平面内任意一条直线.( )
(2)任何一条直线的一般式都能与其他四种形式互化.( )
(3)关于的二元一次方程(不同时为)一定表示直线.( )
(4)对于二元一次方程,当时,方程表示斜率
不存在的直线.( )
【答案】
问题2:在方程中,为何值时,方程表示的直线:
①平行于轴 ②平行于轴 ③与轴重合 ④与轴重合 ⑤过原点
解析:
① 当A=0,B≠0,C≠0时,方程表示的直线与 x 轴平行;
② 当B=0,A≠0,C≠0 时,方程表示的直线与 y 轴平行;
③ 当 A=0,B≠0,C=0时,方程表示的直线与 x 轴重合 ;
④ 当 B=0,A≠0,C=0 时,方程表示的直线与 y 轴重合;
⑤ 当C=0时,方程表示的直线过原点.
4. 已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解:因为,
所以点斜式方程为,
斜截式方程为,
整理得一般式方程为,
直线在x轴上的截距为,在y轴上的截距为.
知识点拨:
在x轴上的截距,令y=0;
在y轴上的截距,令x=0.
问题3:如果直线的 l1,l2 的一般式方程为, , 若 l1 与 l2 平行,则A1,A2,B1,B2,C1,C2
应满足什么条件呢?相交呢?垂直呢?重合呢?
(i)若且,l1//l2;
(ii)若,l1 与 l2 相交;
(iii)若A1A2+B1B2=0,l1⊥l2;
(iv),l1 与 l2 重合.
5.(1)已知直线与直线平行,求的值;
(2)当为何值时,直线与直线互相垂直?
解:(1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,∴的值为或.
(2)当为何值时,直线与直线互相垂直?
解:(2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
直线平行、垂直问题技巧:
1. 直线:,直线:,
(1)若l1∥l2 或 A1B2-A2B1=0 且 A1C2-A2C1≠0;
(2)若l1⊥l2 A1A2+B1B2=0.
2.(1)与直线 Ax+By+C=0 平行的直线方程可设为 Ax+By+m=0(m≠C);
(2)与直线 Ax+By+C=0 垂直的直线方程可设为 Bx-Ay+m=0.
6.已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解:(1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.将点代入上式得.
∴所求直线的方程为.
点斜式 斜截式 两点式 截距式 一般式
直线方程 Ax+By+C=0
(A,B不同时为0)
已知条件 直线上一定点
,斜率 斜率k, y轴截距b 直线上两点 (x1,y1),(x2,y2) 非零截距a,b 系数
适用条件 斜率存在 斜率存在 斜率存在且不为 斜率存在且不为,不过原点 任何位置
直线的方程
2.2.3 直线的一般式方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系;
2.能正确地进行直线的一般式方程与特殊形式的方程的转化;
3.能运用直线的一般式方程解决有关问题.
形式 方程 适用条件
点斜式 斜率存在的直线
斜截式 斜率存在的直线
两点式 斜率存在且不为
截距式 斜率存在且不为,不过原点
直线的方程
问题1:由下列各条件,写出直线的方程,并画出图形.
(1)斜率是,经过点;
(2)在轴和轴上的截距分别是,;
(3)经过两点,;
(4)在轴上的截距是,倾斜角是.
【答案】 (1);(2)=1;
(3); (4).
同一直线
都可以化简为
思考1:平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗?
直线
斜率存在
斜率
不存在
0
都可以用,(,不同时为)表示
追问:反之,任意一个关于的二元一次方程都表示一条直线吗?
(,不同时为)
过点
垂直于轴
任意一个关于的二元一次方程都表示一条直线
我们把关于的二元一次方程
(其中,不同时为0)叫做直线的一般式方程,简称一般式.
注:①当时,方程可化为,则 是斜率, 是y轴上的截距;
②当时,方程可化为,表示过点,且垂直于x轴的直线.
一般式方程的结构特征:
①要满足A 、B不能同时为0;
②一般式结构特点:左边“x,y,常数依次排列”,右边为“0”;
③可以表示任意直线;
④A>0,A 、B 、C一般是非分式.
1. 斜率为,且在轴上截距为的直线的一般式方程是( )
. .
. .
2. 在直角坐标系中,直线的倾斜角是( )
. . . .
C
C
3.判断正误(正确的打“√”,错误的打“×”)
(1)直线的一般式方程可以表示平面内任意一条直线.( )
(2)任何一条直线的一般式都能与其他四种形式互化.( )
(3)关于的二元一次方程(不同时为)一定表示直线.( )
(4)对于二元一次方程,当时,方程表示斜率
不存在的直线.( )
【答案】
问题2:在方程中,为何值时,方程表示的直线:
①平行于轴 ②平行于轴 ③与轴重合 ④与轴重合 ⑤过原点
解析:
① 当A=0,B≠0,C≠0时,方程表示的直线与 x 轴平行;
② 当B=0,A≠0,C≠0 时,方程表示的直线与 y 轴平行;
③ 当 A=0,B≠0,C=0时,方程表示的直线与 x 轴重合 ;
④ 当 B=0,A≠0,C=0 时,方程表示的直线与 y 轴重合;
⑤ 当C=0时,方程表示的直线过原点.
4. 已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解:因为,
所以点斜式方程为,
斜截式方程为,
整理得一般式方程为,
直线在x轴上的截距为,在y轴上的截距为.
知识点拨:
在x轴上的截距,令y=0;
在y轴上的截距,令x=0.
问题3:如果直线的 l1,l2 的一般式方程为, , 若 l1 与 l2 平行,则A1,A2,B1,B2,C1,C2
应满足什么条件呢?相交呢?垂直呢?重合呢?
(i)若且,l1//l2;
(ii)若,l1 与 l2 相交;
(iii)若A1A2+B1B2=0,l1⊥l2;
(iv),l1 与 l2 重合.
5.(1)已知直线与直线平行,求的值;
(2)当为何值时,直线与直线互相垂直?
解:(1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,∴的值为或.
(2)当为何值时,直线与直线互相垂直?
解:(2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
直线平行、垂直问题技巧:
1. 直线:,直线:,
(1)若l1∥l2 或 A1B2-A2B1=0 且 A1C2-A2C1≠0;
(2)若l1⊥l2 A1A2+B1B2=0.
2.(1)与直线 Ax+By+C=0 平行的直线方程可设为 Ax+By+m=0(m≠C);
(2)与直线 Ax+By+C=0 垂直的直线方程可设为 Bx-Ay+m=0.
6.已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解:(1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.将点代入上式得.
∴所求直线的方程为.
点斜式 斜截式 两点式 截距式 一般式
直线方程 Ax+By+C=0
(A,B不同时为0)
已知条件 直线上一定点
,斜率 斜率k, y轴截距b 直线上两点 (x1,y1),(x2,y2) 非零截距a,b 系数
适用条件 斜率存在 斜率存在 斜率存在且不为 斜率存在且不为,不过原点 任何位置
直线的方程
