1.4.3 一元二次不等式的应用 课件 (共20 张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 1.4.3 一元二次不等式的应用 课件 (共20 张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:38:37 | ||
图片预览





文档简介
(共20张PPT)
1.4.3 一元二次不等式的应用
1.能从实际情境中抽象出一元二次不等式,并应用一元二次不等式解决实际问题.
“基建狂魔”
01.港珠澳大桥(世界最长的跨海大桥)
02.北盘江大桥(世界上最高的桥)
03.南水北调工程(世界上最大的水利工程)
复习巩固
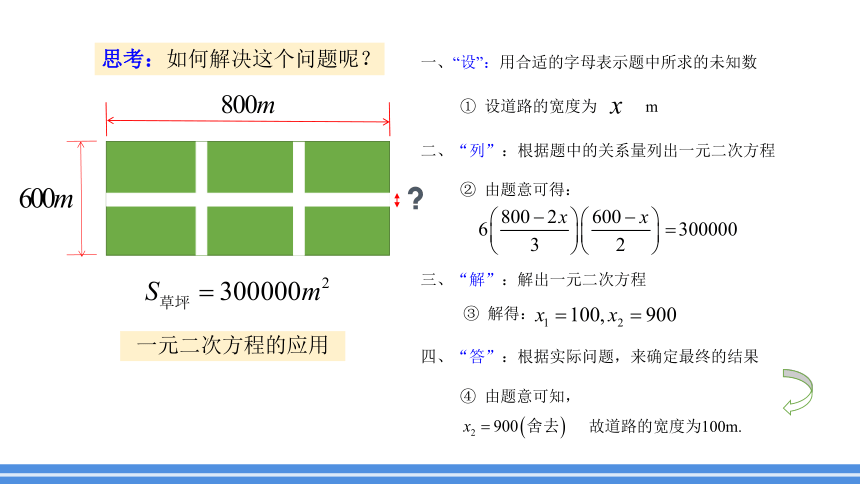
问题1:某施工单位在对一个长 ,宽 的草坪进行绿化时,是这样想的:要修筑同样宽的三条道路(两条纵向,一条横向,且相互垂直),把草坪分为六块大小相等的小草坪,要保证草坪的面积为 ,试求:道路的宽度是多少?
一元二次方程的应用
思考:如何解决这个问题呢?
一、“设”:用合适的字母表示题中所求的未知数
设道路的宽度为 m
二、“列”:根据题中的关系量列出一元二次方程
由题意可得:
三、“解”:解出一元二次方程
解得:
四、“答”:根据实际问题,来确定最终的结果
由题意可知,
故道路的宽度为100m.
总结归纳
一元二次方程的实际应用的一般步骤:
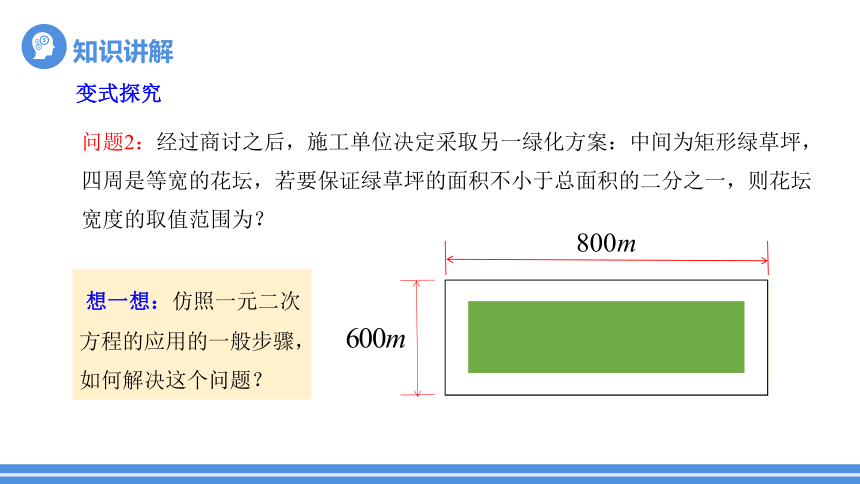
变式探究
问题2:经过商讨之后,施工单位决定采取另一绿化方案:中间为矩形绿草坪,四周是等宽的花坛,若要保证绿草坪的面积不小于总面积的二分之一,则花坛宽度的取值范围为?
想一想:仿照一元二次方程的应用的一般步骤,如何解决这个问题?
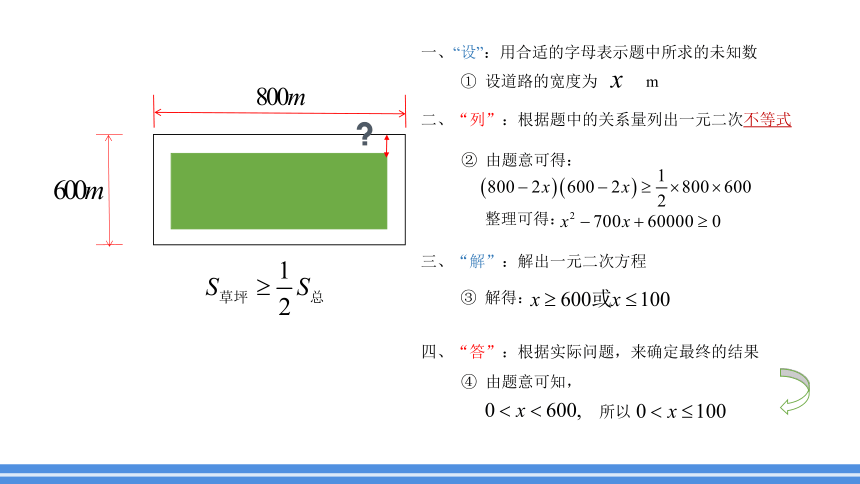
一、“设”:用合适的字母表示题中所求的未知数
设道路的宽度为 m
二、“列”:根据题中的关系量列出一元二次不等式
由题意可得:
三、“解”:解出一元二次方程
解得:
整理可得:
四、“答”:根据实际问题,来确定最终的结果
由题意可知,
所以
对比总结
一元二次方程的应用与一元二次不等式应用的对比
一元二次方程的应用 一元二次不等式的应用
设出未知数 设出未知数
根据题中的等量关系列出等式 根据题中的不等关系列出不等式
解一元二次方程 解一元二次不等式
当出现“至多”“至少”,“取值范围”等字样时,一般使用不等式来解决
知识运用1:销售问题
北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。
问题3:该商品原来每件售价为25元,年销售8万件。
(1)据市场调查,若价格每提高一元,销售量将相应地减少2000件,要使销售的总收入不低于原收入,该商品每件的定价最多为多少元?
知识回顾(销售问题)
销售问题当中的常见定义
进价:商家购进商品时的价格 售价:商家售出商品时的销售价格
成本:商家购入商品所投入的总金额成本=进价×商品总数 收入:商家所卖商品所获得的总金额收入=售价×销售商品总数
利润:商家在销售商品时所赚的钱 利润=收入-成本=(售价-成本)×销售商品总数
问题3:该商品原来每件售价为25元,年销售8万件。
(1)据市场调查,若价格每提高一元,销售量将相应地减少2000件,要使销售的总收入不低于原收入,该商品每件的定价最多为多少元?
解:设商品每件的定价为x元,依题意可得:
整理可得:
解得:
所以要使销售的总收入不低于原收入,每件的定价最多为40元
问题3:该商品原来每件售价为25元,年销售8万件。
解:依题意可得: 时,
整理可得:
故当该商品改革后的销售量至少达到10.2万件时,才能使改革后的销售收入不低于原收入与总投入之和,此时该商品的定价为30元 。
(2)为了抓住申奥契机,扩大该产品的影响力,公司决定将定价提高到 元,拟投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用。试问:当商品改革后的销售量a达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?此时该商品每件定价多少元?
知识运用2:税率问题
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低 个百分点,预测收购量可增加 个百分点 .
(1)写出降税后税收 (万元)与 的关系式
百分率问题当中的常见定义
增长率:增加的数额与原来的数额的比例关系 增长率=(增量÷原总量)×100% 降低率:减少的数额与原来数额的比例的关系:
降低率=(减少量÷原总量)×100%
增长量:一定时期内增长的数量 增长量=原总量×增长率 减少量:一定时期内减少的数量
减少量=原总量×降低率
征税率:应纳税额与征税对象数额之间的比例 征税率=(应纳税额÷征税对象数额)×100%
知识回顾(百分率问题)
解:降税后的税率为 ,农产品的收购量为 万担,依题意得
知识运用2:税率问题
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低 个百分点,预测收购量可增加 个百分点 .
(1)写出降税后税收 (万元)与 的关系式
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低
个百分点,预测收购量可增加 个百分点.
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围。
依题意得:
化简可得:
又因为
解:原计划税收为:
练习:某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月份至十月份销售总额至少达到7000万元,则x的最小值是多少?
则一月份至十月份销售总额为:
依题意得:
令
整理可得:
解得
故:
解:依题意可得:
七月份的销售额为 ,八月份的销售额为
1.4.3 一元二次不等式的应用
1.能从实际情境中抽象出一元二次不等式,并应用一元二次不等式解决实际问题.
“基建狂魔”
01.港珠澳大桥(世界最长的跨海大桥)
02.北盘江大桥(世界上最高的桥)
03.南水北调工程(世界上最大的水利工程)
复习巩固
问题1:某施工单位在对一个长 ,宽 的草坪进行绿化时,是这样想的:要修筑同样宽的三条道路(两条纵向,一条横向,且相互垂直),把草坪分为六块大小相等的小草坪,要保证草坪的面积为 ,试求:道路的宽度是多少?
一元二次方程的应用
思考:如何解决这个问题呢?
一、“设”:用合适的字母表示题中所求的未知数
设道路的宽度为 m
二、“列”:根据题中的关系量列出一元二次方程
由题意可得:
三、“解”:解出一元二次方程
解得:
四、“答”:根据实际问题,来确定最终的结果
由题意可知,
故道路的宽度为100m.
总结归纳
一元二次方程的实际应用的一般步骤:
变式探究
问题2:经过商讨之后,施工单位决定采取另一绿化方案:中间为矩形绿草坪,四周是等宽的花坛,若要保证绿草坪的面积不小于总面积的二分之一,则花坛宽度的取值范围为?
想一想:仿照一元二次方程的应用的一般步骤,如何解决这个问题?
一、“设”:用合适的字母表示题中所求的未知数
设道路的宽度为 m
二、“列”:根据题中的关系量列出一元二次不等式
由题意可得:
三、“解”:解出一元二次方程
解得:
整理可得:
四、“答”:根据实际问题,来确定最终的结果
由题意可知,
所以
对比总结
一元二次方程的应用与一元二次不等式应用的对比
一元二次方程的应用 一元二次不等式的应用
设出未知数 设出未知数
根据题中的等量关系列出等式 根据题中的不等关系列出不等式
解一元二次方程 解一元二次不等式
当出现“至多”“至少”,“取值范围”等字样时,一般使用不等式来解决
知识运用1:销售问题
北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。
问题3:该商品原来每件售价为25元,年销售8万件。
(1)据市场调查,若价格每提高一元,销售量将相应地减少2000件,要使销售的总收入不低于原收入,该商品每件的定价最多为多少元?
知识回顾(销售问题)
销售问题当中的常见定义
进价:商家购进商品时的价格 售价:商家售出商品时的销售价格
成本:商家购入商品所投入的总金额成本=进价×商品总数 收入:商家所卖商品所获得的总金额收入=售价×销售商品总数
利润:商家在销售商品时所赚的钱 利润=收入-成本=(售价-成本)×销售商品总数
问题3:该商品原来每件售价为25元,年销售8万件。
(1)据市场调查,若价格每提高一元,销售量将相应地减少2000件,要使销售的总收入不低于原收入,该商品每件的定价最多为多少元?
解:设商品每件的定价为x元,依题意可得:
整理可得:
解得:
所以要使销售的总收入不低于原收入,每件的定价最多为40元
问题3:该商品原来每件售价为25元,年销售8万件。
解:依题意可得: 时,
整理可得:
故当该商品改革后的销售量至少达到10.2万件时,才能使改革后的销售收入不低于原收入与总投入之和,此时该商品的定价为30元 。
(2)为了抓住申奥契机,扩大该产品的影响力,公司决定将定价提高到 元,拟投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用。试问:当商品改革后的销售量a达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?此时该商品每件定价多少元?
知识运用2:税率问题
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低 个百分点,预测收购量可增加 个百分点 .
(1)写出降税后税收 (万元)与 的关系式
百分率问题当中的常见定义
增长率:增加的数额与原来的数额的比例关系 增长率=(增量÷原总量)×100% 降低率:减少的数额与原来数额的比例的关系:
降低率=(减少量÷原总量)×100%
增长量:一定时期内增长的数量 增长量=原总量×增长率 减少量:一定时期内减少的数量
减少量=原总量×降低率
征税率:应纳税额与征税对象数额之间的比例 征税率=(应纳税额÷征税对象数额)×100%
知识回顾(百分率问题)
解:降税后的税率为 ,农产品的收购量为 万担,依题意得
知识运用2:税率问题
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低 个百分点,预测收购量可增加 个百分点 .
(1)写出降税后税收 (万元)与 的关系式
问题4:某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点)计划可收购 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低
个百分点,预测收购量可增加 个百分点.
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围。
依题意得:
化简可得:
又因为
解:原计划税收为:
练习:某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月份至十月份销售总额至少达到7000万元,则x的最小值是多少?
则一月份至十月份销售总额为:
依题意得:
令
整理可得:
解得
故:
解:依题意可得:
七月份的销售额为 ,八月份的销售额为
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
