3.3.2 指数函数的图象和性质 课件 (共28 张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 3.3.2 指数函数的图象和性质 课件 (共28 张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 916.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:39:51 | ||
图片预览








文档简介
(共28张PPT)
第三章
3.3.2 指数函数的图象和性质
1.掌握指数函数的图象与性质及其简单应用.
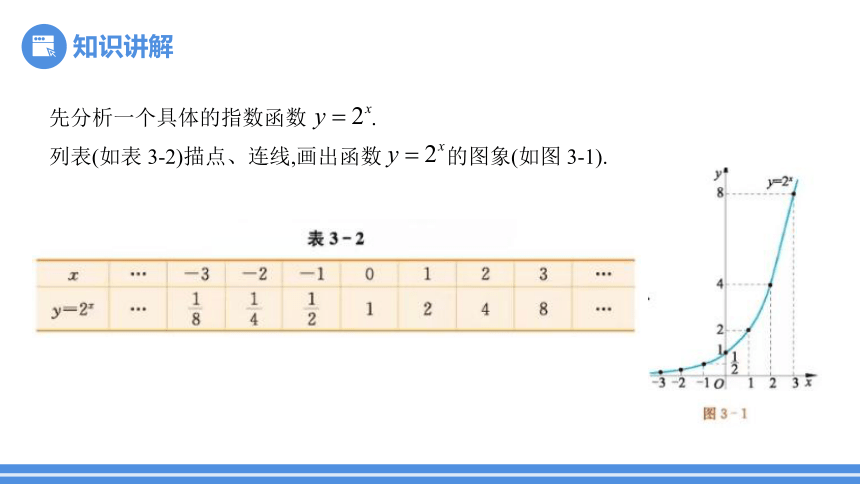
先分析一个具体的指数函数 .
列表(如表 3-2)描点、连线,画出函数 的图象(如图 3-1).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧贴近x轴的位置逐渐上升,过点(0,1),继续上升,
函数值越来越大,图象越来越陡,直至无穷.
由此得到函数 的性质:函数 在R上是增函数,
且值域是(0,+∞).
再分析函数 .
列表(如表 3- 3)、描点、连线,画出函数 的图象(如图3-2).
从图象可以看出:函数 的图象也是位于x轴的上方;
从最侧贴近x轴的位置逐渐上升,过点(0,1),继续上升,数值越
来函数值越来越大,图象越来越陡,直至无穷.
由此得到函数 的性质:函数 在 R上是增函数,
且值域是(0,+∞).
由此可见函数 与 的性质是类似的.
在同一平面直角坐标系中画出函数 与
的图象(如图3-3 ),
可以看出:在y轴左侧函数 的图象在函数
的图象下方;在y轴右侧,函数 的图象在函数
的图象上方.
一般地,当a>1时,指数函数 的定义域是 R,值域是(0,+∞),过定点(0,1),
在R上是增函数.当x值趋近于正无穷大时,函数值趋近于正无穷大;当x值趋近
于负无穷大时,函数值趋近于 0.
对于函数 和 (a>b>1);
例1 比较下列各题中两个数的大小:
(1)因为函数 在R上是增函数,且0.8>0.7,所以
(2)因为函数 在R上是增函数,且一0.15<-0.1,所以
解析:
例2 (1)求使不等式 成立的实数x的集合;
(2)已知方程 ,求实数x的值
(1)因为 , 所以原不等式可化为 .
因为函数 在R上是增函数,所以2x>5,即 x .
因此,使不等式 成立的实数x 的
集合是 .
(2)因为 ,所以原方程可化为
因为函数 在R上是增函数,所以2x-2=5, 即
解析:
前面研究了指数函数 (a>1)的图象和性质,那么当0<a<1时,函数 又会有怎样的图象和性质呢
先分指数函数 .
列表(如表 3-4)、描点、连线,画出函数 的图象(如图3-4).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧无穷远处逐渐下降过点(0,1),继续下降,越来越贴
近x轴.
由此得到函数 的性质:函数 在 R上是
减函数,且值域是(0,+∞).
先分指数函数 .
列表(如表 3-5)、描点、连线,画出函数 的图象(如图3-4).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧无穷远处逐渐下降过点(0,1),继续下降,越来越贴
近x轴.
由此得到函数 的性质:函数 在 R上是
减函数,且值域是(0,+∞).
在同一平面直角坐标系中画出函数 与 的
性质的图象(如图3-6),
可以看出:在y轴左侧,函数 的图象在函数
的图象上方;
在y轴右侧,函数 的图象在函数 的图象上方.
一般地,当0对于函数 和 (0例3 比较下列各题中两个数的大小:
(1)因为函数 在R上是减函数,且-1.8>-2.8,所以
(2)因为函数 在R上是减函数,且一0.3<1.3,所以
解析:
例4 求下列函数的值域:
x∈[-1,+∞).
(1)因为 而函数 的值域是(0,+∞),所以函
数 的值域为(0,+∞);
(2)因为 而函数 在上是减函数,
所以函数 的值域为 ,即(0,27].
解析:
综上所述,指数函数的图象和性质如表 3-6:
归纳:
我们将函数 和 放在一起来研究.
方法1 列表(如表 3-7).
再用描点法在同一平面直角坐标系中画出上述两个函
数的图象(如图 3-7).
观察图象可知,函数 的图象与函数 的
图象关于y轴对称。
方法2 将函数 的解析式改写为 的形式.
记 为y=f(x),那么 (就可以记为y=f(-x).
而函数y=f(x)的图象与函数 y=f(-x)的图象关于y轴对称。
以上两种方法均可得出:函数 与函数 的
图象关于y 轴对称,且它们的单调性相反.
一般地,指数函数 和 (a>0,且a≠1)的图关于y对称且它们在 R上的单调性相反.
例5 比较下列各题中两个数的大小:
利用指数函数的性质对两个数进行比较.
(1)设 ,则函数f(x)在 R上是增函数,
函数g(x)在 R上是减函数,
由指数函数的性质可知 f(0.6)>f(0)=1,而 g(1.6)所以 .
解析:
(2)设 ,则函数f(x) 在R上是减函数,函数 g(x)在R上是
增函数, 由指数函数的性质可知
而 所以
1.当 a>1 时,a的值越大,y 轴右侧的图像越靠近y轴.当 02.比较两个指数式值大小的主要方法
(1)比较形如 的大小,可运用指数型函数 的单调性.
(2)比较形如 的大小,一般找一个“中间值 c”,
第三章
3.3.2 指数函数的图象和性质
1.掌握指数函数的图象与性质及其简单应用.
先分析一个具体的指数函数 .
列表(如表 3-2)描点、连线,画出函数 的图象(如图 3-1).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧贴近x轴的位置逐渐上升,过点(0,1),继续上升,
函数值越来越大,图象越来越陡,直至无穷.
由此得到函数 的性质:函数 在R上是增函数,
且值域是(0,+∞).
再分析函数 .
列表(如表 3- 3)、描点、连线,画出函数 的图象(如图3-2).
从图象可以看出:函数 的图象也是位于x轴的上方;
从最侧贴近x轴的位置逐渐上升,过点(0,1),继续上升,数值越
来函数值越来越大,图象越来越陡,直至无穷.
由此得到函数 的性质:函数 在 R上是增函数,
且值域是(0,+∞).
由此可见函数 与 的性质是类似的.
在同一平面直角坐标系中画出函数 与
的图象(如图3-3 ),
可以看出:在y轴左侧函数 的图象在函数
的图象下方;在y轴右侧,函数 的图象在函数
的图象上方.
一般地,当a>1时,指数函数 的定义域是 R,值域是(0,+∞),过定点(0,1),
在R上是增函数.当x值趋近于正无穷大时,函数值趋近于正无穷大;当x值趋近
于负无穷大时,函数值趋近于 0.
对于函数 和 (a>b>1);
例1 比较下列各题中两个数的大小:
(1)因为函数 在R上是增函数,且0.8>0.7,所以
(2)因为函数 在R上是增函数,且一0.15<-0.1,所以
解析:
例2 (1)求使不等式 成立的实数x的集合;
(2)已知方程 ,求实数x的值
(1)因为 , 所以原不等式可化为 .
因为函数 在R上是增函数,所以2x>5,即 x .
因此,使不等式 成立的实数x 的
集合是 .
(2)因为 ,所以原方程可化为
因为函数 在R上是增函数,所以2x-2=5, 即
解析:
前面研究了指数函数 (a>1)的图象和性质,那么当0<a<1时,函数 又会有怎样的图象和性质呢
先分指数函数 .
列表(如表 3-4)、描点、连线,画出函数 的图象(如图3-4).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧无穷远处逐渐下降过点(0,1),继续下降,越来越贴
近x轴.
由此得到函数 的性质:函数 在 R上是
减函数,且值域是(0,+∞).
先分指数函数 .
列表(如表 3-5)、描点、连线,画出函数 的图象(如图3-4).
从图象可以看出:函数 的图象位于x轴的上方;
从最左侧无穷远处逐渐下降过点(0,1),继续下降,越来越贴
近x轴.
由此得到函数 的性质:函数 在 R上是
减函数,且值域是(0,+∞).
在同一平面直角坐标系中画出函数 与 的
性质的图象(如图3-6),
可以看出:在y轴左侧,函数 的图象在函数
的图象上方;
在y轴右侧,函数 的图象在函数 的图象上方.
一般地,当0
(1)因为函数 在R上是减函数,且-1.8>-2.8,所以
(2)因为函数 在R上是减函数,且一0.3<1.3,所以
解析:
例4 求下列函数的值域:
x∈[-1,+∞).
(1)因为 而函数 的值域是(0,+∞),所以函
数 的值域为(0,+∞);
(2)因为 而函数 在上是减函数,
所以函数 的值域为 ,即(0,27].
解析:
综上所述,指数函数的图象和性质如表 3-6:
归纳:
我们将函数 和 放在一起来研究.
方法1 列表(如表 3-7).
再用描点法在同一平面直角坐标系中画出上述两个函
数的图象(如图 3-7).
观察图象可知,函数 的图象与函数 的
图象关于y轴对称。
方法2 将函数 的解析式改写为 的形式.
记 为y=f(x),那么 (就可以记为y=f(-x).
而函数y=f(x)的图象与函数 y=f(-x)的图象关于y轴对称。
以上两种方法均可得出:函数 与函数 的
图象关于y 轴对称,且它们的单调性相反.
一般地,指数函数 和 (a>0,且a≠1)的图关于y对称且它们在 R上的单调性相反.
例5 比较下列各题中两个数的大小:
利用指数函数的性质对两个数进行比较.
(1)设 ,则函数f(x)在 R上是增函数,
函数g(x)在 R上是减函数,
由指数函数的性质可知 f(0.6)>f(0)=1,而 g(1.6)
解析:
(2)设 ,则函数f(x) 在R上是减函数,函数 g(x)在R上是
增函数, 由指数函数的性质可知
而 所以
1.当 a>1 时,a的值越大,y 轴右侧的图像越靠近y轴.当 0
(1)比较形如 的大小,可运用指数型函数 的单调性.
(2)比较形如 的大小,一般找一个“中间值 c”,
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
