2.4.1 圆的标准方程 课件(共17张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.4.1 圆的标准方程 课件(共17张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 377.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:40:06 | ||
图片预览




文档简介
(共17张PPT)
2.4.1 圆的标准方程
学习目标
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的位置关系.
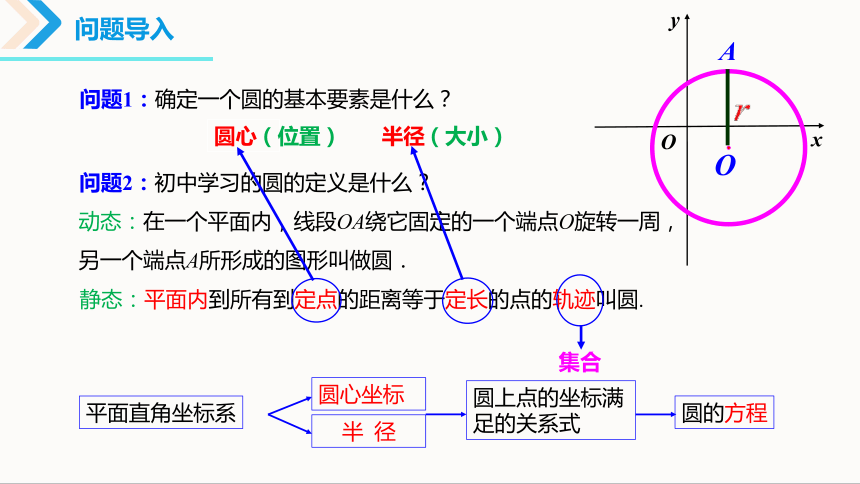
问题导入
问题2:初中学习的圆的定义是什么?
圆心
动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:平面内到所有到定点的距离等于定长的点的轨迹叫圆.
集合
问题1:确定一个圆的基本要素是什么?
半径
(位置)
(大小)
x
y
O
平面直角坐标系
圆心坐标
半 径
圆上点的坐标满足的关系式
圆的方程
新课讲授
两边平方,得
(3)根据 公式,得
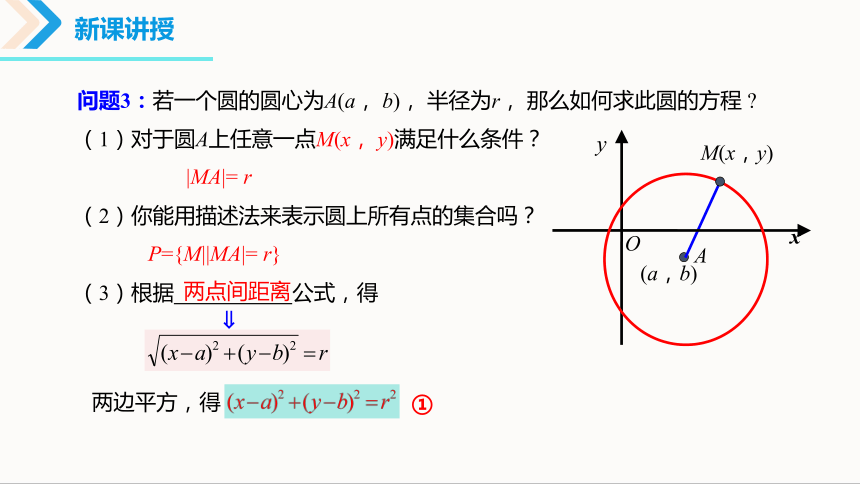
问题3:若一个圆的圆心为A(a, b), 半径为r, 那么如何求此圆的方程
(1)对于圆A上任意一点M(x, y)满足什么条件?
|MA|= r
O
A
M(x,y)
x
(a,b)
①
(2)你能用描述法来表示圆上所有点的集合吗?
P={M||MA|= r}
两点间距离
方程①.
圆上任意点M的坐标
满足
M的坐标满足方程①
点M在圆心为A的圆上
这时我们把方程①称为以圆心为A(a,b), 半径为r的圆的标准方程.
问题4:圆上的点是否都适合方程①?适合方程①的坐标的点是否都在圆上?
①
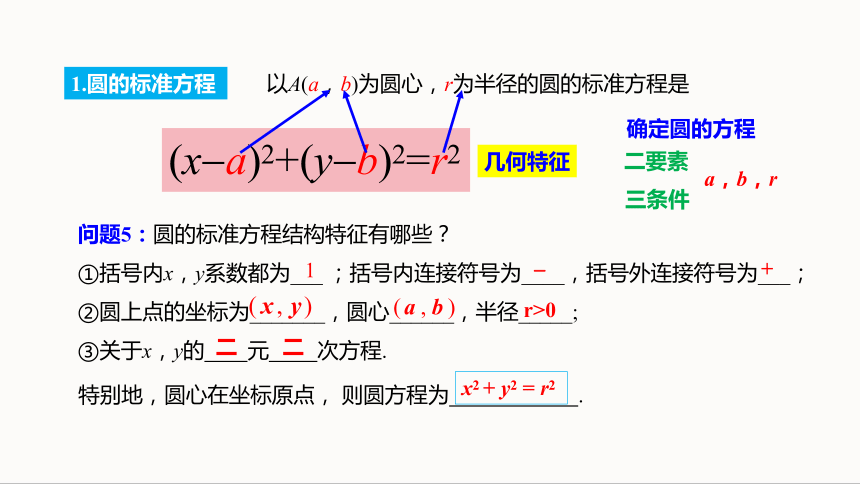
几何特征
三条件
二要素
确定圆的方程
a,b,r
1.圆的标准方程
(x a)2+(y b)2=r2
以A(a,b)为圆心,r为半径的圆的标准方程是
问题5:圆的标准方程结构特征有哪些?
①括号内x,y系数都为___ ;括号内连接符号为____,括号外连接符号为___;
②圆上点的坐标为_______,圆心______,半径_____;
③关于x,y的 元 次方程.
+
r>0
二
二
1
特别地,圆心在坐标原点, 则圆方程为 .
x2 + y2 = r2
例1 求与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程.
解:∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
练1.已知点A(2,0),B(0,-2),圆C以线段AB为直径,则它的标准方程是( )
A.(x+1)2+(y-1)2=2
B.(x-1)2+(y+1)2=2
C.(x+1)2+(y-1)2=4
D.(x-1)2+(y+1)2=4
B
问题6:如何确定点P(x0, y0)与圆(x a)2+(y b)2=r2的位置关系?
2.点与圆的位置关系
|PC||PC|=r
|PC|>r
点在圆上
点在圆外
点在圆内
位置关系
图形
几何条件
代数形式
P
C
C
P
C
P
解:圆心为A(2,-3),半径为5的圆的标准方程是(x-2)2+(y+3)2=25.
把点M1(5,-7)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(5-2)2+(-7+3)2=25,左右两边相等,点M1的坐标满足圆的方程,所以点M1在这个圆上.
把点M2(-2,-1)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(-2-2)2+(-1+3)2=20,左右两边不相等,
点M2的坐标不满足圆的方程,
所以点M2不在这个圆上(如图).
例2 求圆心为A(2,-3), 半径为5的圆的标准方程, 并判断点M1(5,-7), M2(-2,-1)是否在这个圆上.
练2.(1)已知点P(a,a+1)在圆x2+y2=25的内部,则a的取值范围是( )
A.-4(2)点P(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围( )
A.-11 D.a=±1
A
A
例3 已知圆E经过A(2,3),B(3,2),C(4,3)三点,求圆E的标准方程.
解 设圆E:(x-a)2+(y-b)2=r2,r>0,
∴圆E:(x-3)2+(y-3)2=1.
练3.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
解:方法一 (待定系数法)设圆的标准方程为(x-a)2+(y-b)2=r2,
即圆的标准方程是(x-4)2+(y+3)2=25.
练3.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
∵弦的垂直平分线过圆心,
即圆心坐标为(4,-3),
即圆的标准方程是(x-4)2+(y+3)2=25.
方法二 (几何法)由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
课堂总结
回顾本节课,回答下列问题:
(1)圆的标准方程是什么?
(2)如何判断点与圆的位置关系?
当堂检测
1.圆(x+1)2+(y-2)2=4的圆心、半径是( )
A.(1,-2),4 B.(1,-2),2
C.(-1,2),4 D.(-1,2),2
2.点(5a+1,12a)在圆(x-1)2+y2=1的内部,则实数a的取值范围是( )
D
D
当堂检测
3.已知点A(1,-2),B(-1,4),求过点A,B且圆心在直线2x-y-4=0上的圆的标准方程.
故所求圆的标准方程为(x-3)2+(y-2)2=20.
解:设圆的标准方程为(x-a)2+(y-b)2=r2,
2.4.1 圆的标准方程
学习目标
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的位置关系.
问题导入
问题2:初中学习的圆的定义是什么?
圆心
动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:平面内到所有到定点的距离等于定长的点的轨迹叫圆.
集合
问题1:确定一个圆的基本要素是什么?
半径
(位置)
(大小)
x
y
O
平面直角坐标系
圆心坐标
半 径
圆上点的坐标满足的关系式
圆的方程
新课讲授
两边平方,得
(3)根据 公式,得
问题3:若一个圆的圆心为A(a, b), 半径为r, 那么如何求此圆的方程
(1)对于圆A上任意一点M(x, y)满足什么条件?
|MA|= r
O
A
M(x,y)
x
(a,b)
①
(2)你能用描述法来表示圆上所有点的集合吗?
P={M||MA|= r}
两点间距离
方程①.
圆上任意点M的坐标
满足
M的坐标满足方程①
点M在圆心为A的圆上
这时我们把方程①称为以圆心为A(a,b), 半径为r的圆的标准方程.
问题4:圆上的点是否都适合方程①?适合方程①的坐标的点是否都在圆上?
①
几何特征
三条件
二要素
确定圆的方程
a,b,r
1.圆的标准方程
(x a)2+(y b)2=r2
以A(a,b)为圆心,r为半径的圆的标准方程是
问题5:圆的标准方程结构特征有哪些?
①括号内x,y系数都为___ ;括号内连接符号为____,括号外连接符号为___;
②圆上点的坐标为_______,圆心______,半径_____;
③关于x,y的 元 次方程.
+
r>0
二
二
1
特别地,圆心在坐标原点, 则圆方程为 .
x2 + y2 = r2
例1 求与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程.
解:∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
练1.已知点A(2,0),B(0,-2),圆C以线段AB为直径,则它的标准方程是( )
A.(x+1)2+(y-1)2=2
B.(x-1)2+(y+1)2=2
C.(x+1)2+(y-1)2=4
D.(x-1)2+(y+1)2=4
B
问题6:如何确定点P(x0, y0)与圆(x a)2+(y b)2=r2的位置关系?
2.点与圆的位置关系
|PC|
|PC|>r
点在圆上
点在圆外
点在圆内
位置关系
图形
几何条件
代数形式
P
C
C
P
C
P
解:圆心为A(2,-3),半径为5的圆的标准方程是(x-2)2+(y+3)2=25.
把点M1(5,-7)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(5-2)2+(-7+3)2=25,左右两边相等,点M1的坐标满足圆的方程,所以点M1在这个圆上.
把点M2(-2,-1)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(-2-2)2+(-1+3)2=20,左右两边不相等,
点M2的坐标不满足圆的方程,
所以点M2不在这个圆上(如图).
例2 求圆心为A(2,-3), 半径为5的圆的标准方程, 并判断点M1(5,-7), M2(-2,-1)是否在这个圆上.
练2.(1)已知点P(a,a+1)在圆x2+y2=25的内部,则a的取值范围是( )
A.-4
A.-1
A
A
例3 已知圆E经过A(2,3),B(3,2),C(4,3)三点,求圆E的标准方程.
解 设圆E:(x-a)2+(y-b)2=r2,r>0,
∴圆E:(x-3)2+(y-3)2=1.
练3.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
解:方法一 (待定系数法)设圆的标准方程为(x-a)2+(y-b)2=r2,
即圆的标准方程是(x-4)2+(y+3)2=25.
练3.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
∵弦的垂直平分线过圆心,
即圆心坐标为(4,-3),
即圆的标准方程是(x-4)2+(y+3)2=25.
方法二 (几何法)由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
课堂总结
回顾本节课,回答下列问题:
(1)圆的标准方程是什么?
(2)如何判断点与圆的位置关系?
当堂检测
1.圆(x+1)2+(y-2)2=4的圆心、半径是( )
A.(1,-2),4 B.(1,-2),2
C.(-1,2),4 D.(-1,2),2
2.点(5a+1,12a)在圆(x-1)2+y2=1的内部,则实数a的取值范围是( )
D
D
当堂检测
3.已知点A(1,-2),B(-1,4),求过点A,B且圆心在直线2x-y-4=0上的圆的标准方程.
故所求圆的标准方程为(x-3)2+(y-2)2=20.
解:设圆的标准方程为(x-a)2+(y-b)2=r2,
