4.3.1用一元一次方程解决问题 课件(共28张PPT)
文档属性
| 名称 | 4.3.1用一元一次方程解决问题 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
4.3.1 用一元一次方程解决问题——一般步骤、
销售问题
第4章 一元一次方程
教学目标
01
掌握用一元一次方程解决问题的一般步骤,并能从关键句中找到等量关系,进一步列方程
02
掌握与销售问题有关的基本公式,进一步用一元一次方程解决销售问题
用一元一次方程解决问题的一般步骤
知识精讲
问题——右图中的一套紫砂壶茶具包括1把茶壶和6只茶杯。做1把茶壶需要0.6kg的泥料,做1只茶杯需要0.15kg的泥料。10.5kg泥料可以做几套这样的茶具 (不计制作时的耗损)
01
课堂引入
知识精讲
【算术方法】
0.6+6×0.15=1.5(kg),
10.5÷1.5=7(套),
答:可以做7套茶具。
01
课堂引入
【列方程方法】
设可做x套茶具,
根据题意得:0.6x+6×0.15x=10.5,
解得:x=7,
答:可以做7套茶具。
知识精讲
01
课堂引入
比较小明、小丽的方法,你能说说他们是如何思考的吗
上述问题中,小丽利用列方程方法解决问题,经历了如下过程:
1.根据题意,设一个合适的未知数。
2.根据问题中的等量关系,列出方程.
设可做x套茶具
茶壶泥料+茶杯泥料=总泥料
0.6x +6×0.15x=10.5
审题
3.解方程,求出未知数的值。
4.写出问题的答案。
x=7
答:可以做7套茶具.
审题
设未知数
列方程
解方程
检验
答
02
知识精讲
必须要有检验的过程:
检验未知数的值是否满足方程,
检验该值在实际问题中是否有意义。
02
知识精讲
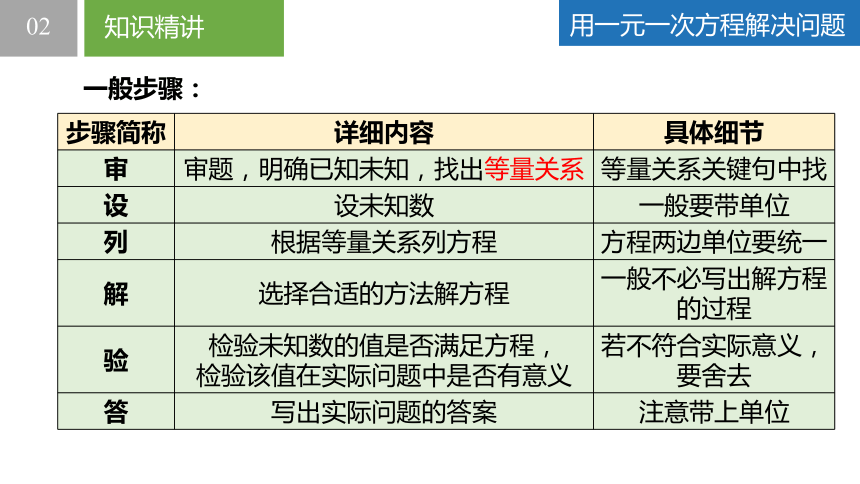
用一元一次方程解决问题
一般步骤:
步骤简称 详细内容 具体细节
审
设
列
解
验
答
审题,明确已知未知,找出等量关系 等量关系关键句中找
设未知数 一般要带单位
根据等量关系列方程 方程两边单位要统一
选择合适的方法解方程 一般不必写出解方程的过程
检验未知数的值是否满足方程, 检验该值在实际问题中是否有意义 若不符合实际意义,要舍去
写出实际问题的答案 注意带上单位
今年小明13岁,王老师45岁,再过几年小明年龄是王老师年龄的三分之一
02
知识精讲
审题
【分析】这个问题中的等量关系:
若干年后小明年龄=若干年后王老师年龄×
解:设再过x年小明年龄是王老师年龄的三分之一,
根据题意得:13+x=(45+x),
解得:x=3,
答:3年后小明年龄是王老师年龄的三分之一。
讨论——请你尝试用算术方法解上题,并与列方程方法比较,
你认为列方程方法有什么优势
02
知识精讲
【算术方法】
45-13×3=6(岁),6÷(3-1)=3(年),
答:3年后小明年龄是王老师年龄的三分之一。
45岁
13岁
02
知识精讲
列方程的优势:
未知数直接参加运算,顺向思维列方程即可,思路简单直观。
例1、A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B种饮料单价为x元/瓶,那么下面所列方程正确的是( )
A.2(x-1)+3x=13 B.2(x+1)+3x=13
C.2x+3(x+1)=13 D.2x+3(x-1)=13
A
解:设B种饮料单价为x元/瓶,则A种饮料单价为(x-1)元/瓶,
根据题意得:2(x-1)+3x=13。
03
典例精析
注意:
由于x-1后面带单位,所以要给它加上括号~
例2、一个两位数,个位数字与十位数字的和为9,如果将个位数字与十位数字对调后所得新数比原数小9,则原两位数是( )
A.45 B.27 C.72 D.54
解:设原数的个位数字是x,则十位数字是9-x,
根据题意得:10x+(9-x)-[10(9-x)+x]=9,
解得:x=5,9-x=4,
答:原数为54。
03
典例精析
D
问 题 目 录
销售问题
??问题
??问题
……
生活中,我们经常可以在各种售货平台看见一些商品优惠信息~
商家真的会少赚吗?
01
情境引入
Q1:要想知道商家有没有少赚,我们需要知道什么?
成本价
(进价)
标价
优惠活动
(折扣)
售价
利润
利润率
01
情境引入
Q2:上述的基本量之间有什么样的关系呢?
01
情境引入
单件利润=单价售价-单件进价;
单价售价=单件标价×(打折数/10×100%) ;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
02
知识精讲
销售问题的有关公式
单价售价=单件标价×(打折数/10×100%);
单件利润=单价售价-单件进价;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
解:设这种服装每件的进价是x元,
8折,
即×80%
例1、一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
【分析】等量关系:单件售价-单件进价=15
03
典例精析
进价/件 标价/件 售价/件
x
适当画表更清楚哦~
x(1+40%) x(1+40%)×80%
解:设这种服装每件的进价是x元,
根据题意得:x(1+40%)×80%-x=15,
解得:x=125,
答:这种服装每件的进价是125元。
03
典例精析
解:设甲种商品的原单价为x元,则乙种商品的原单价为(100-x)元,
例2、甲、乙两种商品的单价之和为100元,因为季节变化,甲商品降价10%,乙商品提价5%,调价后,甲、乙两商品的单价之和比原计划之和提高2%,求甲、乙两种商品的原来单价?
【分析】等量关系:现单价之和=100×(1+2%)
原单价 现单价
甲 x
乙 100-x
合计 100
03
典例精析
(1-10%)x
(1+5%)(100-x)
(1-10%)x+(1+5%)(100-x)
解:设甲种商品的原单价为x元,则乙种商品的原单价为(100-x)元,
根据题意得:(1-10%)x+(1+5%)(100-x)=100×(1+2%),
解得:x=20,则100-x=80,
答:甲种商品的原单价为20元,则乙种商品的原单价为80元。
03
典例精析
解:设电器每台定价为x元,则每台进价为(x-48)元,
例3、某商场按定价销售某种电器时,每台获利48元,按定价的9折销售该电器6台与将定价降低30元销售该电器9台所获得的利润相等,该电器每台进价、定价各是多少元?
【分析】等量关系:销售6台的利润=销售9台的利润
进价/台 定价/台 售价/台 利润/台
方式一 x-48 x
方式二
03
典例精析
90%x 48-10%x
x-30 18
03
典例精析
解:设电器每台定价为x元,则每台进价为(x-48)元,
根据题意得:(48-10%x)×6=18×9,
解得:x=210,则x-48=162,
答:电器每台进价为162元,每台定价为210元。
解:设甲服装成本是x元,则乙服装成本是(500-x)元,
例4、甲乙两件衣服的成本共500元,商店老板为获取利润,决定将家服装按50%的利润定价,乙服装按40%的利润定价,在实际销售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲乙两件服装成本各是多少元?
【分析】等量关系:销售总收入-进货总成本=157
03
典例精析
03
典例精析
成本 定价 售价
甲 x
乙 500-x 合计 500
解:设甲服装成本x元,则乙服装成本(500-x)元,
根据题意得:[150%x+140%(500-x)]×90%-500=157,
解得:x=300,则500-x=200,
答:甲服装成本300元,则乙服装成本200元。
150%x
140%(500-x) 150%x+140%(500-x) [150%x+140%(500-x)]×90%
课后总结
用一元一次方程解决问题的一般步骤:
步骤简称 详细内容 具体细节
审 审题,明确已知未知,找出等量关系 等量关系关键句中找
设 设未知数 一般要带单位
列 根据等量关系列方程 方程两边单位要统一
解 选择合适的方法解方程 一般不必写出解方程的过程
验 检验未知数的值是否满足方程, 检验该值在实际问题中是否有意义 若不符合实际意义,要舍去
答 写出实际问题的答案 注意带上单位
课后总结
销售问题的有关公式:
单价售价=单件标价×(打折数/10×100%);
单件利润=单价售价-单件进价;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
4.3.1 用一元一次方程解决问题——一般步骤、
销售问题
第4章 一元一次方程
教学目标
01
掌握用一元一次方程解决问题的一般步骤,并能从关键句中找到等量关系,进一步列方程
02
掌握与销售问题有关的基本公式,进一步用一元一次方程解决销售问题
用一元一次方程解决问题的一般步骤
知识精讲
问题——右图中的一套紫砂壶茶具包括1把茶壶和6只茶杯。做1把茶壶需要0.6kg的泥料,做1只茶杯需要0.15kg的泥料。10.5kg泥料可以做几套这样的茶具 (不计制作时的耗损)
01
课堂引入
知识精讲
【算术方法】
0.6+6×0.15=1.5(kg),
10.5÷1.5=7(套),
答:可以做7套茶具。
01
课堂引入
【列方程方法】
设可做x套茶具,
根据题意得:0.6x+6×0.15x=10.5,
解得:x=7,
答:可以做7套茶具。
知识精讲
01
课堂引入
比较小明、小丽的方法,你能说说他们是如何思考的吗
上述问题中,小丽利用列方程方法解决问题,经历了如下过程:
1.根据题意,设一个合适的未知数。
2.根据问题中的等量关系,列出方程.
设可做x套茶具
茶壶泥料+茶杯泥料=总泥料
0.6x +6×0.15x=10.5
审题
3.解方程,求出未知数的值。
4.写出问题的答案。
x=7
答:可以做7套茶具.
审题
设未知数
列方程
解方程
检验
答
02
知识精讲
必须要有检验的过程:
检验未知数的值是否满足方程,
检验该值在实际问题中是否有意义。
02
知识精讲
用一元一次方程解决问题
一般步骤:
步骤简称 详细内容 具体细节
审
设
列
解
验
答
审题,明确已知未知,找出等量关系 等量关系关键句中找
设未知数 一般要带单位
根据等量关系列方程 方程两边单位要统一
选择合适的方法解方程 一般不必写出解方程的过程
检验未知数的值是否满足方程, 检验该值在实际问题中是否有意义 若不符合实际意义,要舍去
写出实际问题的答案 注意带上单位
今年小明13岁,王老师45岁,再过几年小明年龄是王老师年龄的三分之一
02
知识精讲
审题
【分析】这个问题中的等量关系:
若干年后小明年龄=若干年后王老师年龄×
解:设再过x年小明年龄是王老师年龄的三分之一,
根据题意得:13+x=(45+x),
解得:x=3,
答:3年后小明年龄是王老师年龄的三分之一。
讨论——请你尝试用算术方法解上题,并与列方程方法比较,
你认为列方程方法有什么优势
02
知识精讲
【算术方法】
45-13×3=6(岁),6÷(3-1)=3(年),
答:3年后小明年龄是王老师年龄的三分之一。
45岁
13岁
02
知识精讲
列方程的优势:
未知数直接参加运算,顺向思维列方程即可,思路简单直观。
例1、A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B种饮料单价为x元/瓶,那么下面所列方程正确的是( )
A.2(x-1)+3x=13 B.2(x+1)+3x=13
C.2x+3(x+1)=13 D.2x+3(x-1)=13
A
解:设B种饮料单价为x元/瓶,则A种饮料单价为(x-1)元/瓶,
根据题意得:2(x-1)+3x=13。
03
典例精析
注意:
由于x-1后面带单位,所以要给它加上括号~
例2、一个两位数,个位数字与十位数字的和为9,如果将个位数字与十位数字对调后所得新数比原数小9,则原两位数是( )
A.45 B.27 C.72 D.54
解:设原数的个位数字是x,则十位数字是9-x,
根据题意得:10x+(9-x)-[10(9-x)+x]=9,
解得:x=5,9-x=4,
答:原数为54。
03
典例精析
D
问 题 目 录
销售问题
??问题
??问题
……
生活中,我们经常可以在各种售货平台看见一些商品优惠信息~
商家真的会少赚吗?
01
情境引入
Q1:要想知道商家有没有少赚,我们需要知道什么?
成本价
(进价)
标价
优惠活动
(折扣)
售价
利润
利润率
01
情境引入
Q2:上述的基本量之间有什么样的关系呢?
01
情境引入
单件利润=单价售价-单件进价;
单价售价=单件标价×(打折数/10×100%) ;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
02
知识精讲
销售问题的有关公式
单价售价=单件标价×(打折数/10×100%);
单件利润=单价售价-单件进价;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
解:设这种服装每件的进价是x元,
8折,
即×80%
例1、一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
【分析】等量关系:单件售价-单件进价=15
03
典例精析
进价/件 标价/件 售价/件
x
适当画表更清楚哦~
x(1+40%) x(1+40%)×80%
解:设这种服装每件的进价是x元,
根据题意得:x(1+40%)×80%-x=15,
解得:x=125,
答:这种服装每件的进价是125元。
03
典例精析
解:设甲种商品的原单价为x元,则乙种商品的原单价为(100-x)元,
例2、甲、乙两种商品的单价之和为100元,因为季节变化,甲商品降价10%,乙商品提价5%,调价后,甲、乙两商品的单价之和比原计划之和提高2%,求甲、乙两种商品的原来单价?
【分析】等量关系:现单价之和=100×(1+2%)
原单价 现单价
甲 x
乙 100-x
合计 100
03
典例精析
(1-10%)x
(1+5%)(100-x)
(1-10%)x+(1+5%)(100-x)
解:设甲种商品的原单价为x元,则乙种商品的原单价为(100-x)元,
根据题意得:(1-10%)x+(1+5%)(100-x)=100×(1+2%),
解得:x=20,则100-x=80,
答:甲种商品的原单价为20元,则乙种商品的原单价为80元。
03
典例精析
解:设电器每台定价为x元,则每台进价为(x-48)元,
例3、某商场按定价销售某种电器时,每台获利48元,按定价的9折销售该电器6台与将定价降低30元销售该电器9台所获得的利润相等,该电器每台进价、定价各是多少元?
【分析】等量关系:销售6台的利润=销售9台的利润
进价/台 定价/台 售价/台 利润/台
方式一 x-48 x
方式二
03
典例精析
90%x 48-10%x
x-30 18
03
典例精析
解:设电器每台定价为x元,则每台进价为(x-48)元,
根据题意得:(48-10%x)×6=18×9,
解得:x=210,则x-48=162,
答:电器每台进价为162元,每台定价为210元。
解:设甲服装成本是x元,则乙服装成本是(500-x)元,
例4、甲乙两件衣服的成本共500元,商店老板为获取利润,决定将家服装按50%的利润定价,乙服装按40%的利润定价,在实际销售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲乙两件服装成本各是多少元?
【分析】等量关系:销售总收入-进货总成本=157
03
典例精析
03
典例精析
成本 定价 售价
甲 x
乙 500-x 合计 500
解:设甲服装成本x元,则乙服装成本(500-x)元,
根据题意得:[150%x+140%(500-x)]×90%-500=157,
解得:x=300,则500-x=200,
答:甲服装成本300元,则乙服装成本200元。
150%x
140%(500-x) 150%x+140%(500-x) [150%x+140%(500-x)]×90%
课后总结
用一元一次方程解决问题的一般步骤:
步骤简称 详细内容 具体细节
审 审题,明确已知未知,找出等量关系 等量关系关键句中找
设 设未知数 一般要带单位
列 根据等量关系列方程 方程两边单位要统一
解 选择合适的方法解方程 一般不必写出解方程的过程
验 检验未知数的值是否满足方程, 检验该值在实际问题中是否有意义 若不符合实际意义,要舍去
答 写出实际问题的答案 注意带上单位
课后总结
销售问题的有关公式:
单价售价=单件标价×(打折数/10×100%);
单件利润=单价售价-单件进价;
利润率=单件利润/单件进价×100%;
总利润=销售总收入-进货总成本。
同课章节目录
