青岛版六年级下册数学3.2正比例关系 课件(共15张PPT)
文档属性
| 名称 | 青岛版六年级下册数学3.2正比例关系 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 06:48:18 | ||
图片预览






文档简介
(共15张PPT)
3.2正比例关系
青岛版小学6年级下册
第三章《啤酒生产中的数学》
一、学习目标
能够通过实际例子的引入对正比例关系有初步的认识;
会判断两个数量在什么情况下以及为什么存在正比例关系;
能够通过表格、图像、方程、图表以及文字描述中的比例关系说出比例关系的图像上点 的含义,特别是点 和 ( 为单位比率),能够结合图像解释清楚图像变化快慢的实际意义;
2
二、问题导入
案例1:如图是某啤酒生产车间的一角,表格里出示了啤酒生产中工作总量和对应的工作时间,观察表格中数据的变化情况,找出其中变化的量与不变的量。
啤酒生产情况记录
时间(时) 0 1 2 3 4 5 6 7 ...
总(吨) 0 15 30 45 60 75 90 105 ...
在这个表格里,工作时间和工作总量这两个量都在变化,并且是两种相关联的量。
工作时间变化,工作总量也随着变化,但是工作总量与工作时间的比值有什么特点?
比值是一定的,即工作总量/工作时间=工作效率k(不变)。
二、问题导入
案例2: 一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
时间/时 1 2 3 4 5 6 7
路程/千米 90 180 270 360
路程是随着时间的变化而变化的,路程与时间的比值(也就是速度) 是一定的。
=
像上面两个问题中这样,两个相互依赖的量,如果其中的一个量扩大(或缩小)若干倍,另一个量也相应地扩大(或缩小)相同的倍数,这两个量叫做成正比例的量。它们中的变化关系叫做正比例关系。
正比例关系可以用字母关系式表示: (一定)其中 是正常数,通常被称为比例常数。
三、概念形成
6
三、正比例概念
一、 判断下列两种量是否比例关系么?为什么?
(1)长方形的面积一定,它的长和宽。
(2)长方形的周长一定,它的长和宽。
(3)长方形的宽一定,它的面积和长。
7
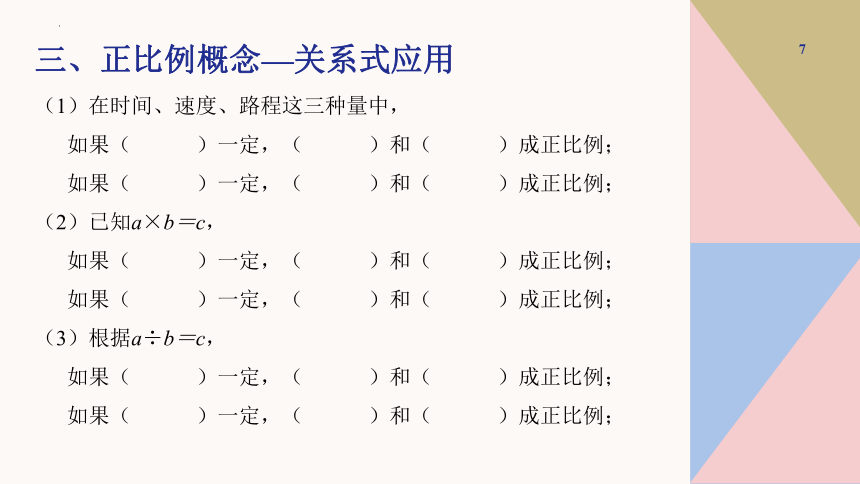
三、正比例概念—关系式应用
(1)在时间、速度、路程这三种量中,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
(2)已知a×b=c,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
(3)根据a÷b=c,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
8
三、正比例概念—辨析
案例:某商场正在进行促销活动,规定消费金额每满100元即可享受10元的折扣。小明在该商场购买了价值300元的商品。
问题:请分析小明实际支付的金额与消费金额之间的关系,并判断这是否是正比例关系。如果不是,请说明理由。
9
三、正比例概念—辨析
小明消费了300元,按照每满100元减10元的规则,他可以享受3次10元的折扣,总共减免30元。
因此,小明实际支付的金额为300元 - 30元 = 270元。
分析关系:虽然折扣金额与消费金额的增长有关,但实际支付金额(270元)与消费金额(300元)之间并不构成直接的正比例关系。因为当消费金额增加时,折扣金额也会增加,但增加的比例(即折扣率)是固定的(10%),而不是消费金额增加的直接比例。所以,这不是一个纯粹的正比例关系。
10
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
(2)根据上图说一说,8吨大麦芽能生产多少吨啤酒?
(3)估计一下,要生产55吨啤酒需要多少吨大麦芽?
分析:观察,我们发现啤酒总量是随着大麦芽的增多而增多的,并且啤酒总量与大麦芽的比值是个定值。
11
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
从图中我们可以发现,随着大麦芽吨数的增加,啤酒的总量也在不断增加。
这表明啤酒的生产量与所需的大麦芽数量之间存在正相关关系。
此外,观察图表中的数据点,我们可以发现啤酒总量与大麦芽的数量之间的比例似乎是一个定值,即每增加一定数量的大麦芽,啤酒的总量也会相应增加一个固定的比例。
12
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(2)根据上图说一说,8吨大麦芽能生产多少吨啤酒?
先确定图表中啤酒总量与大麦芽数量之间的比例关系。由于图表中没有直接给出具体的比例数值,我们需要通过图表中的数据点进行估算。我们可以选择一个或几个数据点来估算斜率(即比例)。比例大约为1:10,那么8吨大麦芽大约能生产80吨啤酒。
13
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(3)估计一下,要生产55吨啤酒需要多少吨大麦芽?
为了估计生产55吨啤酒需要多少吨大麦芽,我们需要知道啤酒总量与大麦芽数量之间的确切比例。如果假设比例仍然为1:10(或根据实际数据点调整比例),那么生产55吨啤酒大约需要5.5吨大麦芽。
14
四、比例关系实践应用--2
长沙造纸厂的生产情况如下表,根据表回答问题。
时间(天) 1 2 3 4 5 6 7 …
生产量(吨) 70 140 210 280 350 420 490 …
(1)表中相关联的量是 和 ;
(2)根据表中的数据,写出一个比例 。
(3)表中相关联的两种量成 关系。
(5)估计生产550吨纸片,大约需要 天
谢谢
3.2正比例关系
青岛版小学6年级下册
第三章《啤酒生产中的数学》
一、学习目标
能够通过实际例子的引入对正比例关系有初步的认识;
会判断两个数量在什么情况下以及为什么存在正比例关系;
能够通过表格、图像、方程、图表以及文字描述中的比例关系说出比例关系的图像上点 的含义,特别是点 和 ( 为单位比率),能够结合图像解释清楚图像变化快慢的实际意义;
2
二、问题导入
案例1:如图是某啤酒生产车间的一角,表格里出示了啤酒生产中工作总量和对应的工作时间,观察表格中数据的变化情况,找出其中变化的量与不变的量。
啤酒生产情况记录
时间(时) 0 1 2 3 4 5 6 7 ...
总(吨) 0 15 30 45 60 75 90 105 ...
在这个表格里,工作时间和工作总量这两个量都在变化,并且是两种相关联的量。
工作时间变化,工作总量也随着变化,但是工作总量与工作时间的比值有什么特点?
比值是一定的,即工作总量/工作时间=工作效率k(不变)。
二、问题导入
案例2: 一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
时间/时 1 2 3 4 5 6 7
路程/千米 90 180 270 360
路程是随着时间的变化而变化的,路程与时间的比值(也就是速度) 是一定的。
=
像上面两个问题中这样,两个相互依赖的量,如果其中的一个量扩大(或缩小)若干倍,另一个量也相应地扩大(或缩小)相同的倍数,这两个量叫做成正比例的量。它们中的变化关系叫做正比例关系。
正比例关系可以用字母关系式表示: (一定)其中 是正常数,通常被称为比例常数。
三、概念形成
6
三、正比例概念
一、 判断下列两种量是否比例关系么?为什么?
(1)长方形的面积一定,它的长和宽。
(2)长方形的周长一定,它的长和宽。
(3)长方形的宽一定,它的面积和长。
7
三、正比例概念—关系式应用
(1)在时间、速度、路程这三种量中,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
(2)已知a×b=c,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
(3)根据a÷b=c,
如果( )一定,( )和( )成正比例;
如果( )一定,( )和( )成正比例;
8
三、正比例概念—辨析
案例:某商场正在进行促销活动,规定消费金额每满100元即可享受10元的折扣。小明在该商场购买了价值300元的商品。
问题:请分析小明实际支付的金额与消费金额之间的关系,并判断这是否是正比例关系。如果不是,请说明理由。
9
三、正比例概念—辨析
小明消费了300元,按照每满100元减10元的规则,他可以享受3次10元的折扣,总共减免30元。
因此,小明实际支付的金额为300元 - 30元 = 270元。
分析关系:虽然折扣金额与消费金额的增长有关,但实际支付金额(270元)与消费金额(300元)之间并不构成直接的正比例关系。因为当消费金额增加时,折扣金额也会增加,但增加的比例(即折扣率)是固定的(10%),而不是消费金额增加的直接比例。所以,这不是一个纯粹的正比例关系。
10
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
(2)根据上图说一说,8吨大麦芽能生产多少吨啤酒?
(3)估计一下,要生产55吨啤酒需要多少吨大麦芽?
分析:观察,我们发现啤酒总量是随着大麦芽的增多而增多的,并且啤酒总量与大麦芽的比值是个定值。
11
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
从图中我们可以发现,随着大麦芽吨数的增加,啤酒的总量也在不断增加。
这表明啤酒的生产量与所需的大麦芽数量之间存在正相关关系。
此外,观察图表中的数据点,我们可以发现啤酒总量与大麦芽的数量之间的比例似乎是一个定值,即每增加一定数量的大麦芽,啤酒的总量也会相应增加一个固定的比例。
12
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(2)根据上图说一说,8吨大麦芽能生产多少吨啤酒?
先确定图表中啤酒总量与大麦芽数量之间的比例关系。由于图表中没有直接给出具体的比例数值,我们需要通过图表中的数据点进行估算。我们可以选择一个或几个数据点来估算斜率(即比例)。比例大约为1:10,那么8吨大麦芽大约能生产80吨啤酒。
13
四、比例关系实践应用--1
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(3)估计一下,要生产55吨啤酒需要多少吨大麦芽?
为了估计生产55吨啤酒需要多少吨大麦芽,我们需要知道啤酒总量与大麦芽数量之间的确切比例。如果假设比例仍然为1:10(或根据实际数据点调整比例),那么生产55吨啤酒大约需要5.5吨大麦芽。
14
四、比例关系实践应用--2
长沙造纸厂的生产情况如下表,根据表回答问题。
时间(天) 1 2 3 4 5 6 7 …
生产量(吨) 70 140 210 280 350 420 490 …
(1)表中相关联的量是 和 ;
(2)根据表中的数据,写出一个比例 。
(3)表中相关联的两种量成 关系。
(5)估计生产550吨纸片,大约需要 天
谢谢
