2.1.2 两条直线平行和垂直的判定 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.1.2 两条直线平行和垂直的判定 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 11:34:57 | ||
图片预览






文档简介
(共18张PPT)
2.1.2 两条直线平行和垂直的判定
1. 能根据斜率判定两条直线平行或垂直.(重点)
2. 能应用两条直线平行或垂直的关系解决相应的几何问题.
(重点、难点)
2024年7月19日济宁方特东方欲晓主题乐园开园迎客,这也是全国第4座、山东省第1座方特东方欲晓园区。里面的过山车是一项富有刺激性的娱乐项目.为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直,你能感受到过山车中的平行和垂直吗?两条直线的平行与垂直用什么来刻画呢?
问题1 我们知道,平面中的两条直线有两种位置关系:相交、平行.
如图,若l1∥ l2,则倾斜角分别为α1=α2,所以tan α1=tan α2,即k1=k2.
因此,若l1∥ l2,即k1=k2.
反之,若k1=k2,则tan α1=tan α2,所以α1=α2所以l1∥ l2.
因此,对于斜率分别为k1,k2的两条直线l1,l2,有
l1//l2 k1=k2.
问题2 当两条直线l1与l2平行时,它们的斜率k1与k2满足什么关系?并论证你的结论.
注意:若没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
追问:若直线的斜率不存在,与什么位置关系?
若直线重合,此时仍然有. (这个结论常用于证明三点共线)
注 意
直线的斜率不存在
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 l1∥l2 两直线的斜率都不存在
图示
k1=k2
两条直线平行的判定
用斜率证明三点共线时,常常用到这个结论。
知识总结
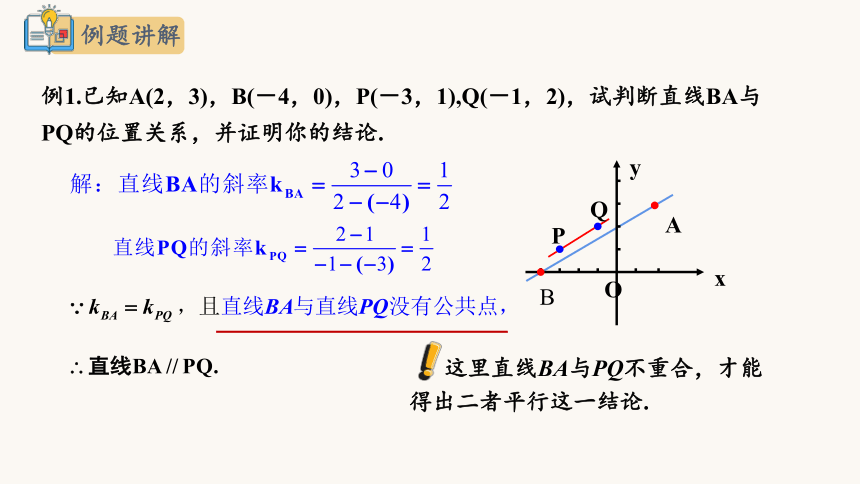
例1.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
例题讲解
这里直线BA与PQ不重合,才能得出二者平行这一结论.
例2.四边形ABCD四个顶点为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并证明.
x
y
O
B
C
D
是否还有其他方法
例题讲解
A
使用斜率公式判定两直线平行的步骤
看斜率
相等?
提醒:若已知直线上点的坐标,判断直线是否平行时,要考虑直线重合的情况.
平行
平行
不平行
都不存在
是
否
归纳总结
问题3:当直线l1,l2垂直时,它们的斜率除了不相等外,是否还有特殊的数量关系?
设两条直线的斜率存在,分别为,则:
的方向向量分别是,,
即:.
问题4.当两条直线垂直时,它们的斜率之积一定等于-1吗 为什么
直线l 2的斜率不存在,如图,当直线l1的倾斜角为0°时,若l1⊥ l2,则l2的倾斜角为90°,其斜率不存在.
两条垂直直线斜率之间的关系
类型 斜率都存在 l1(或l2)的斜率不存在
前提条件 α1≠90°,且α2≠90° α1=90°(或α2=90°)
对应关系 l1⊥l2 l1⊥l2 l2(或l1)的斜率为0
图示
k1k2=1
知识总结
例3.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
分析 结合图形可猜想AB⊥BC,△ABC为直角三角形.
直线BC 的斜率
解:直线AB 的斜率
∴AB⊥BC,即∠ABC=90°
∴△ABC为直角三角形.
是否还有其他方法
例题讲解
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式对参数进行讨论.
提醒:若已知点的坐标含有参数,利用两条直线的垂直关系求参数值时,要注意讨论斜率是否存在.
使用斜率公式判定两直线垂直的步骤
归纳总结
1.若直线l1的倾斜角为135°,直线l2经过点P(-2,-1),Q(3,-6),则直线l1与l2的位置关系是( )
A.垂直 B.平行 C.重合 D.平行或重合
D
2.若直线l经过点(a-2,-1)和(-a-2,1),且与斜率为 的直线垂直,则实数a的值是( )
A
3.已知在平行四边形ABCD 中,A(1,2),B(5,0),C(3,4).
(1)求点D的坐标.
(2)试判断平行四边形ABCD是否为菱形.
两直线平行于垂直的判定
平行
垂直
斜率相等
斜率都不存在
斜率之积等于-1
一条直线斜率为0,另一条斜率不存在
2.1.2 两条直线平行和垂直的判定
1. 能根据斜率判定两条直线平行或垂直.(重点)
2. 能应用两条直线平行或垂直的关系解决相应的几何问题.
(重点、难点)
2024年7月19日济宁方特东方欲晓主题乐园开园迎客,这也是全国第4座、山东省第1座方特东方欲晓园区。里面的过山车是一项富有刺激性的娱乐项目.为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直,你能感受到过山车中的平行和垂直吗?两条直线的平行与垂直用什么来刻画呢?
问题1 我们知道,平面中的两条直线有两种位置关系:相交、平行.
如图,若l1∥ l2,则倾斜角分别为α1=α2,所以tan α1=tan α2,即k1=k2.
因此,若l1∥ l2,即k1=k2.
反之,若k1=k2,则tan α1=tan α2,所以α1=α2所以l1∥ l2.
因此,对于斜率分别为k1,k2的两条直线l1,l2,有
l1//l2 k1=k2.
问题2 当两条直线l1与l2平行时,它们的斜率k1与k2满足什么关系?并论证你的结论.
注意:若没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
追问:若直线的斜率不存在,与什么位置关系?
若直线重合,此时仍然有. (这个结论常用于证明三点共线)
注 意
直线的斜率不存在
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 l1∥l2 两直线的斜率都不存在
图示
k1=k2
两条直线平行的判定
用斜率证明三点共线时,常常用到这个结论。
知识总结
例1.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
例题讲解
这里直线BA与PQ不重合,才能得出二者平行这一结论.
例2.四边形ABCD四个顶点为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并证明.
x
y
O
B
C
D
是否还有其他方法
例题讲解
A
使用斜率公式判定两直线平行的步骤
看斜率
相等?
提醒:若已知直线上点的坐标,判断直线是否平行时,要考虑直线重合的情况.
平行
平行
不平行
都不存在
是
否
归纳总结
问题3:当直线l1,l2垂直时,它们的斜率除了不相等外,是否还有特殊的数量关系?
设两条直线的斜率存在,分别为,则:
的方向向量分别是,,
即:.
问题4.当两条直线垂直时,它们的斜率之积一定等于-1吗 为什么
直线l 2的斜率不存在,如图,当直线l1的倾斜角为0°时,若l1⊥ l2,则l2的倾斜角为90°,其斜率不存在.
两条垂直直线斜率之间的关系
类型 斜率都存在 l1(或l2)的斜率不存在
前提条件 α1≠90°,且α2≠90° α1=90°(或α2=90°)
对应关系 l1⊥l2 l1⊥l2 l2(或l1)的斜率为0
图示
k1k2=1
知识总结
例3.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
分析 结合图形可猜想AB⊥BC,△ABC为直角三角形.
直线BC 的斜率
解:直线AB 的斜率
∴AB⊥BC,即∠ABC=90°
∴△ABC为直角三角形.
是否还有其他方法
例题讲解
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式对参数进行讨论.
提醒:若已知点的坐标含有参数,利用两条直线的垂直关系求参数值时,要注意讨论斜率是否存在.
使用斜率公式判定两直线垂直的步骤
归纳总结
1.若直线l1的倾斜角为135°,直线l2经过点P(-2,-1),Q(3,-6),则直线l1与l2的位置关系是( )
A.垂直 B.平行 C.重合 D.平行或重合
D
2.若直线l经过点(a-2,-1)和(-a-2,1),且与斜率为 的直线垂直,则实数a的值是( )
A
3.已知在平行四边形ABCD 中,A(1,2),B(5,0),C(3,4).
(1)求点D的坐标.
(2)试判断平行四边形ABCD是否为菱形.
两直线平行于垂直的判定
平行
垂直
斜率相等
斜率都不存在
斜率之积等于-1
一条直线斜率为0,另一条斜率不存在
