2.1.1 倾斜角和斜率 课件(共25张PPT)2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.1.1 倾斜角和斜率 课件(共25张PPT)2024~2025学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 12:21:02 | ||
图片预览





文档简介
(共25张PPT)
2.1.2 倾斜角和斜率
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(难点)
2.理解直线的倾斜角和斜率的概念.
3. 掌握求直线斜率的两种方法,并理解推导过程(重难点).
观察图中跷跷板的位置固定吗?我们如何描述某一时刻跷跷板的位置呢?
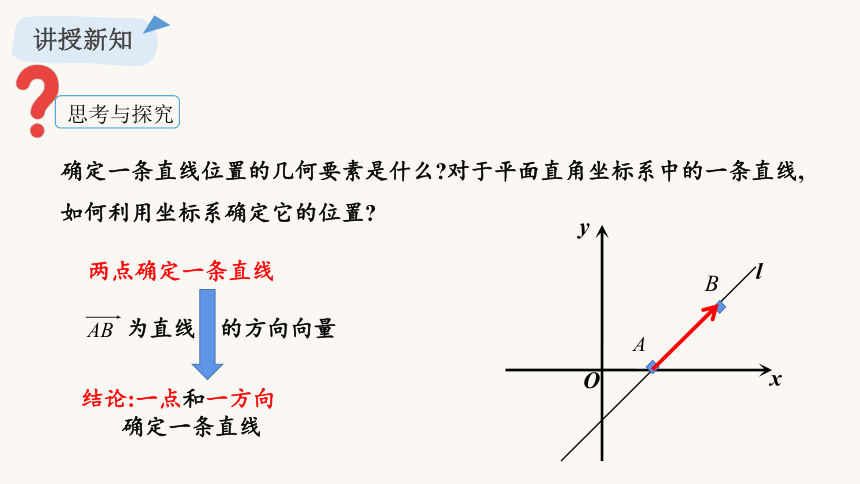
确定一条直线位置的几何要素是什么 对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置
x
y
O
l
两点确定一条直线
结论:一点和一方向
确定一条直线
为直线 的方向向量
思考与探究
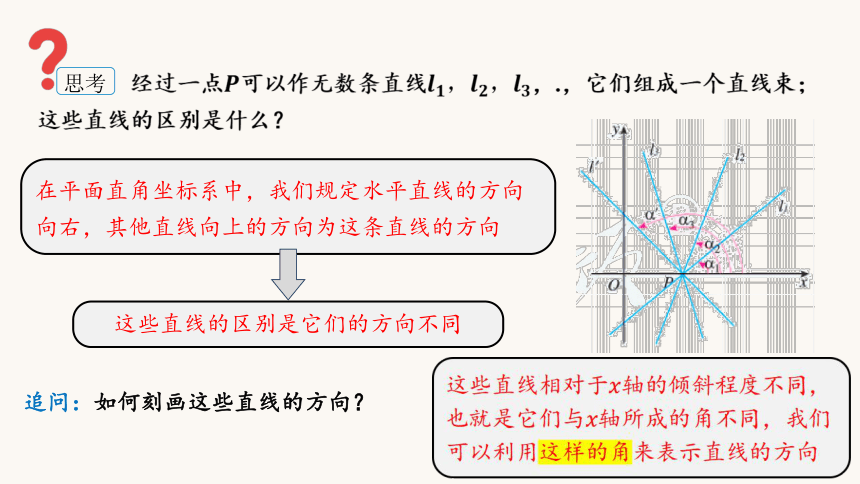
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向
这些直线的区别是它们的方向不同
追问:如何刻画这些直线的方向?
这些直线相对于轴的倾斜程度不同,也就是它们与轴所成的角不同,我们可以利用这样的角来表示直线的方向
经过一点可以作无数条直线,.,它们组成一个直线束;这些直线的区别是什么?
思考
1.定义:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线的倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
定直线的方法有两种:
①直线上两点
②直线上一点和直线的倾斜角
规定倾斜角为0°
规定倾斜角为90°
o
x
y
o
x
y
o
x
y
o
x
y
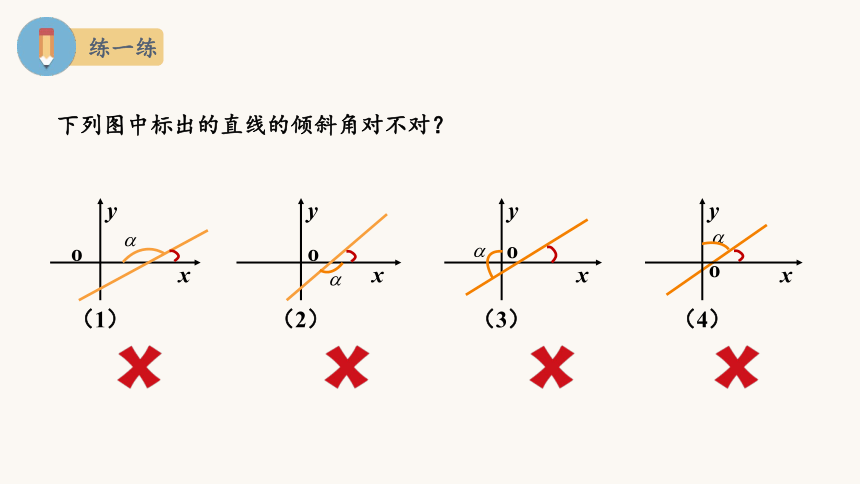
(1)
(2)
(3)
(4)
下列图中标出的直线的倾斜角对不对?
练一练
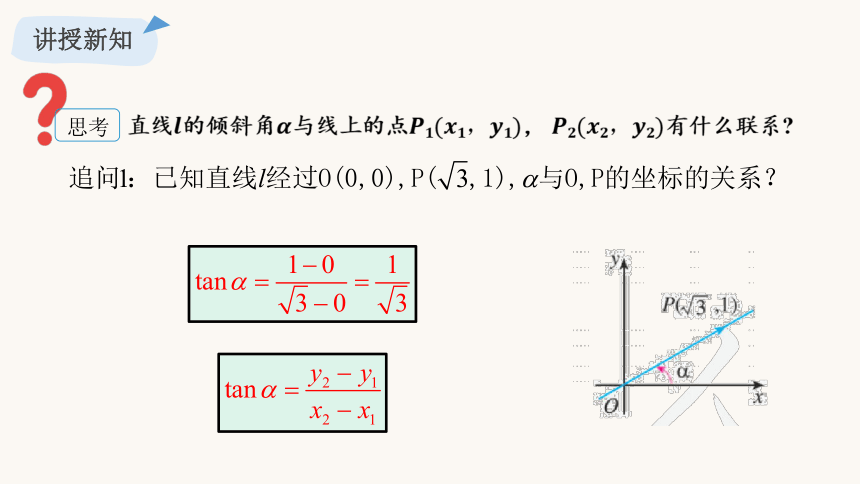
直线的倾斜角与线上的点, 有什么联系
思考
追问2:直线经过,,与的坐标有什么关系?
一般地,如图,当向量 的方向向上时, ,平移向量 到 ,则点 的坐标为 ,且直线 的倾斜角也是 ,由
正切函数的定义,有
能不能构造一个直角三角形去求?
当α为锐角时,
倾斜角是锐角时
当α为钝角时,
倾斜角是钝角时
经过两点
的直线的斜率公式:
(1) 当x1=x2时,公式不适用,此时α=900
(2) 直线的斜率可以通过直线上任意两点的坐标来表示
(3) 与两点的顺序无关
注 意
当直线与轴平行或重合时,上述式子还成立吗?为什么
思考
当直线与x轴平行或重合时:y1=y2,α=0°
上述式子任然成立.
倾斜角是 的直线没有斜率,倾斜角不是 的直线都有斜率.
斜率常用小写字母 表示,即
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
综上:直线 的倾斜角 与直线 上的两点
的坐标有如下关系:
概念总结
为什么倾斜角是的直线没有斜率?
tanα
直线倾斜角为时
分母为
无意义
思考:当直线的倾斜角由逐渐增大到时,其斜率如何变化?
思考
x
y
O
l
直线的方向向量与斜率的关系
直线P1P2的方向向量
直线经过,,斜率时与的顺序有关系吗?
没有关系,tanα
思考
练一练
答案:
练一练
答案:
例1:如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
例题讲解
答案:
答案:
B
1.两个知识点:
3.三个思想
数形结合、分类讨论、从特殊到一般的数学思想.
(2)斜率
(1)倾斜角
2.两个公式
2.1.2 倾斜角和斜率
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(难点)
2.理解直线的倾斜角和斜率的概念.
3. 掌握求直线斜率的两种方法,并理解推导过程(重难点).
观察图中跷跷板的位置固定吗?我们如何描述某一时刻跷跷板的位置呢?
确定一条直线位置的几何要素是什么 对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置
x
y
O
l
两点确定一条直线
结论:一点和一方向
确定一条直线
为直线 的方向向量
思考与探究
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向
这些直线的区别是它们的方向不同
追问:如何刻画这些直线的方向?
这些直线相对于轴的倾斜程度不同,也就是它们与轴所成的角不同,我们可以利用这样的角来表示直线的方向
经过一点可以作无数条直线,.,它们组成一个直线束;这些直线的区别是什么?
思考
1.定义:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线的倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
定直线的方法有两种:
①直线上两点
②直线上一点和直线的倾斜角
规定倾斜角为0°
规定倾斜角为90°
o
x
y
o
x
y
o
x
y
o
x
y
(1)
(2)
(3)
(4)
下列图中标出的直线的倾斜角对不对?
练一练
直线的倾斜角与线上的点, 有什么联系
思考
追问2:直线经过,,与的坐标有什么关系?
一般地,如图,当向量 的方向向上时, ,平移向量 到 ,则点 的坐标为 ,且直线 的倾斜角也是 ,由
正切函数的定义,有
能不能构造一个直角三角形去求?
当α为锐角时,
倾斜角是锐角时
当α为钝角时,
倾斜角是钝角时
经过两点
的直线的斜率公式:
(1) 当x1=x2时,公式不适用,此时α=900
(2) 直线的斜率可以通过直线上任意两点的坐标来表示
(3) 与两点的顺序无关
注 意
当直线与轴平行或重合时,上述式子还成立吗?为什么
思考
当直线与x轴平行或重合时:y1=y2,α=0°
上述式子任然成立.
倾斜角是 的直线没有斜率,倾斜角不是 的直线都有斜率.
斜率常用小写字母 表示,即
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
综上:直线 的倾斜角 与直线 上的两点
的坐标有如下关系:
概念总结
为什么倾斜角是的直线没有斜率?
tanα
直线倾斜角为时
分母为
无意义
思考:当直线的倾斜角由逐渐增大到时,其斜率如何变化?
思考
x
y
O
l
直线的方向向量与斜率的关系
直线P1P2的方向向量
直线经过,,斜率时与的顺序有关系吗?
没有关系,tanα
思考
练一练
答案:
练一练
答案:
例1:如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
例题讲解
答案:
答案:
B
1.两个知识点:
3.三个思想
数形结合、分类讨论、从特殊到一般的数学思想.
(2)斜率
(1)倾斜角
2.两个公式
