2.2.1 直线的点斜式方程 课件(共16张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.1 直线的点斜式方程 课件(共16张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 660.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
2.2.1 直线的点斜式方程
1.掌握直线的点斜式方程和斜截式方程,并会用它们求直线的方程;(重点)
2.了解直线的斜截式方程与一次函数的关系;(重点)
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.(难点)
情景导入
2024年7月30日在巴黎奥运会射击项目中的男子飞碟多向决赛中,齐迎夺得男子飞碟多向银牌,刷新了中国男子飞碟射击选手在奥运赛场的最佳战绩。运动员在该项目训练时,要掌握两个动作要领:一是托枪的手要非常稳,二是眼睛要瞄准目标的方向.若把子弹飞行的轨迹看作一条直线,并且射击手达到了上述的两个动作要求.
(1) 托枪的手的位置相当于直线中哪个几何要素?
(2) 试从数学角度分析子弹是否会命中目标?
思考
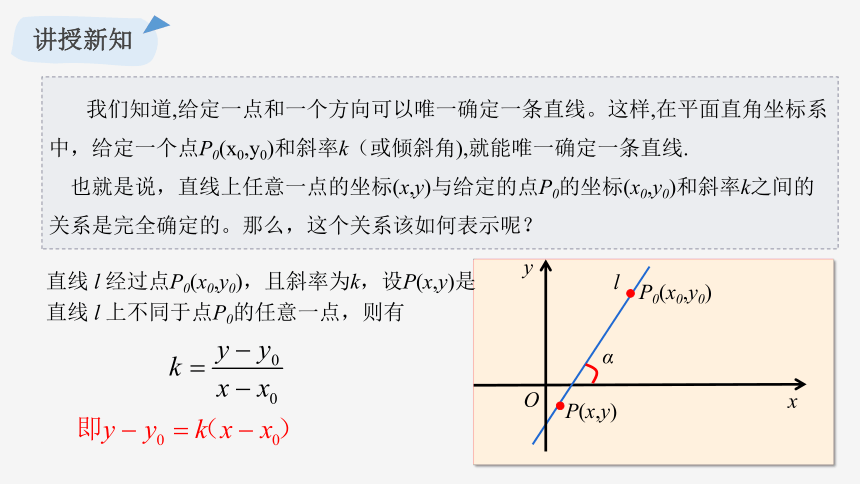
我们知道,给定一点和一个方向可以唯一确定一条直线。这样,在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
也就是说,直线上任意一点的坐标(x,y)与给定的点P0的坐标(x0,y0)和斜率k之间的关系是完全确定的。那么,这个关系该如何表示呢?
l
α
x
y
O
P0(x0,y0)
P(x,y)
直线 l 经过点P0(x0,y0),且斜率为k,设P(x,y)是直线 l 上不同于点P0的任意一点,则有
一、直线的点斜式方程
方程由直线上一个定点(x0,y0)及该直线的斜率 k 确定,我们把它叫做直线的点斜式方程,简称点斜式。
已知直线l经过点(x0, y0),
(1)当直线l的倾斜角为0°时,直线l的方程是什么?
(2)当直线l的倾斜角为90°时,直线l的方程如何表示?
l
x
y
O
P0(x0,y0)
P(x,y)
当倾斜角为0°时,k=0,代入点斜式
l
x
y
O
P0(x0,y0)
P(x,y)
当倾斜角为90°时,没有斜率,不能用点斜式表示,直线上每个点横坐标都为x0,
例1 直线 l 经过点P0(-2,3),且倾斜角α=45°,求直线 l 的点斜式方程,并画出直线 l.
解:直线 l 经过点P0(-2,3),斜率k=tan45°=1,代入点斜式方程得 y-3=x+2.
画图时,再找出直线l上的另一个点P1(x1,y1),例如,取x1=-1,则y1=4,得点P1的坐标为(-1,4),过P0,P1的直线即为所求,如图所示
例题讲解
练一练
练习1 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是;
(2)经过点B(-,2),倾斜角是30
(3)经过点C(0,3),倾斜角是0;
(4)经过点D(-4,-2),倾斜角是.
练一练
练习2 填空题.
(1)已知直线的点斜式方程是y-2=x-1,那么此直线的斜率是______,倾斜角是______;
(2)已知直线的点斜式方程是y+2=(x+1),那么此直线的斜率是_______,倾斜角是______;
1
45°
60°
我们已经学习了直线的点斜式方程的表示,那么若直线经过点P0(0,b),斜率为k,此时直线方程如何表示?
将点P0(0,b)和斜率k代入点斜式方程,得
y-b=k(x-0)
即 y=kx+b
点斜式的一种特殊情形!
二、直线的斜截式方程
我们把直线l与y 轴的交点(0,b)的纵坐标 b 叫做直线l在y轴上的截距,这样,方程y=kx+b由直线的斜率k与它在y轴上的截距b确定。
我们把方程y=kx+b叫做直线的斜截式方程,简称斜截式。
思考1:截距是距离吗?
思考2:一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同
截距不是距离,截距可正,可负,可为零;而距离只能是零或正数。
一次函数的x的系数k≠0,否则就是常函数y=b;直线的斜截式方程y=kx+b中的k可以为0.
思考3:如何从直线方程的角度认识一次函数y=kx+b?
思考4:你能说出一次函数y=2x-1,y=3x及y=-x+3的图象的特点吗?
k 是直线的斜率,b是直线在y轴上的截距
例题讲解
结论:
练一练
练习3 写出下列直线的斜截式方程:
(1)斜率是,在y轴上的截距是-2;
(2)斜率是-2,在y轴上的截距是4.
y = - 2x + 4
练习4 判断下列各对直线是否平行或垂直:
(1)
(2)
平行
垂直
斜截式:
直线 l 经过点P0(0,b),斜率为k
点斜式:
直线 l 经过点P0(x0,y0),斜率为k
y=kx+b
2.2.1 直线的点斜式方程
1.掌握直线的点斜式方程和斜截式方程,并会用它们求直线的方程;(重点)
2.了解直线的斜截式方程与一次函数的关系;(重点)
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.(难点)
情景导入
2024年7月30日在巴黎奥运会射击项目中的男子飞碟多向决赛中,齐迎夺得男子飞碟多向银牌,刷新了中国男子飞碟射击选手在奥运赛场的最佳战绩。运动员在该项目训练时,要掌握两个动作要领:一是托枪的手要非常稳,二是眼睛要瞄准目标的方向.若把子弹飞行的轨迹看作一条直线,并且射击手达到了上述的两个动作要求.
(1) 托枪的手的位置相当于直线中哪个几何要素?
(2) 试从数学角度分析子弹是否会命中目标?
思考
我们知道,给定一点和一个方向可以唯一确定一条直线。这样,在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
也就是说,直线上任意一点的坐标(x,y)与给定的点P0的坐标(x0,y0)和斜率k之间的关系是完全确定的。那么,这个关系该如何表示呢?
l
α
x
y
O
P0(x0,y0)
P(x,y)
直线 l 经过点P0(x0,y0),且斜率为k,设P(x,y)是直线 l 上不同于点P0的任意一点,则有
一、直线的点斜式方程
方程由直线上一个定点(x0,y0)及该直线的斜率 k 确定,我们把它叫做直线的点斜式方程,简称点斜式。
已知直线l经过点(x0, y0),
(1)当直线l的倾斜角为0°时,直线l的方程是什么?
(2)当直线l的倾斜角为90°时,直线l的方程如何表示?
l
x
y
O
P0(x0,y0)
P(x,y)
当倾斜角为0°时,k=0,代入点斜式
l
x
y
O
P0(x0,y0)
P(x,y)
当倾斜角为90°时,没有斜率,不能用点斜式表示,直线上每个点横坐标都为x0,
例1 直线 l 经过点P0(-2,3),且倾斜角α=45°,求直线 l 的点斜式方程,并画出直线 l.
解:直线 l 经过点P0(-2,3),斜率k=tan45°=1,代入点斜式方程得 y-3=x+2.
画图时,再找出直线l上的另一个点P1(x1,y1),例如,取x1=-1,则y1=4,得点P1的坐标为(-1,4),过P0,P1的直线即为所求,如图所示
例题讲解
练一练
练习1 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是;
(2)经过点B(-,2),倾斜角是30
(3)经过点C(0,3),倾斜角是0;
(4)经过点D(-4,-2),倾斜角是.
练一练
练习2 填空题.
(1)已知直线的点斜式方程是y-2=x-1,那么此直线的斜率是______,倾斜角是______;
(2)已知直线的点斜式方程是y+2=(x+1),那么此直线的斜率是_______,倾斜角是______;
1
45°
60°
我们已经学习了直线的点斜式方程的表示,那么若直线经过点P0(0,b),斜率为k,此时直线方程如何表示?
将点P0(0,b)和斜率k代入点斜式方程,得
y-b=k(x-0)
即 y=kx+b
点斜式的一种特殊情形!
二、直线的斜截式方程
我们把直线l与y 轴的交点(0,b)的纵坐标 b 叫做直线l在y轴上的截距,这样,方程y=kx+b由直线的斜率k与它在y轴上的截距b确定。
我们把方程y=kx+b叫做直线的斜截式方程,简称斜截式。
思考1:截距是距离吗?
思考2:一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同
截距不是距离,截距可正,可负,可为零;而距离只能是零或正数。
一次函数的x的系数k≠0,否则就是常函数y=b;直线的斜截式方程y=kx+b中的k可以为0.
思考3:如何从直线方程的角度认识一次函数y=kx+b?
思考4:你能说出一次函数y=2x-1,y=3x及y=-x+3的图象的特点吗?
k 是直线的斜率,b是直线在y轴上的截距
例题讲解
结论:
练一练
练习3 写出下列直线的斜截式方程:
(1)斜率是,在y轴上的截距是-2;
(2)斜率是-2,在y轴上的截距是4.
y = - 2x + 4
练习4 判断下列各对直线是否平行或垂直:
(1)
(2)
平行
垂直
斜截式:
直线 l 经过点P0(0,b),斜率为k
点斜式:
直线 l 经过点P0(x0,y0),斜率为k
y=kx+b
