2.2.3直线的一般方程 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.3直线的一般方程 课件(共18张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 599.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
2.2.3 直线的一般方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系.(重点)
2.能正确地进行直线的一般式方程与特殊形式的方程的转化.(重点)
3.能运用直线的一般式方程解决有关问题.(难点)
复习导入
想一想:我们前面学习的直线方程中都有几个变量
这些方程的共同特征是什么
直线的方程
一点及斜率
直线上两点
点斜式
斜截式
两点式
截距式
直线的方程
点斜式
斜截式
两点式
截距式
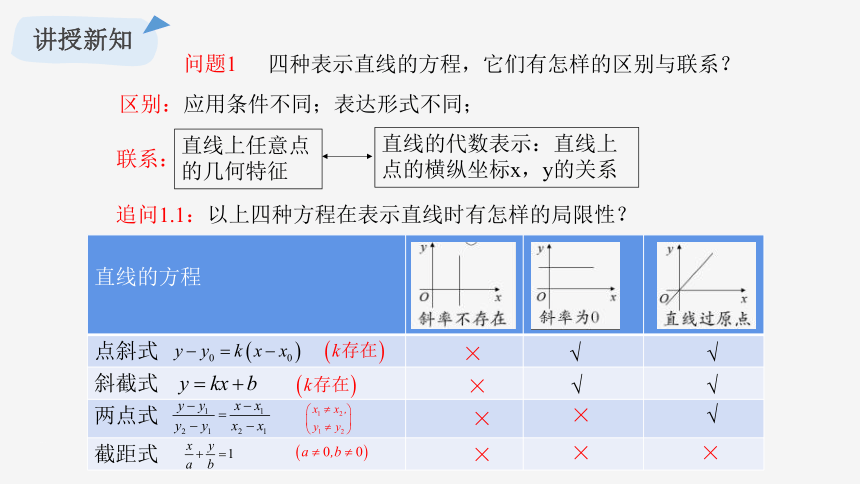
问题1
四种表示直线的方程,它们有怎样的区别与联系?
联系:
直线上任意点的几何特征
直线的代数表示:直线上点的横纵坐标x,y的关系
区别:应用条件不同;表达形式不同;
追问1.1:以上四种方程在表示直线时有怎样的局限性?
×
×
×
×
×
×
×
√
√
√
√
√
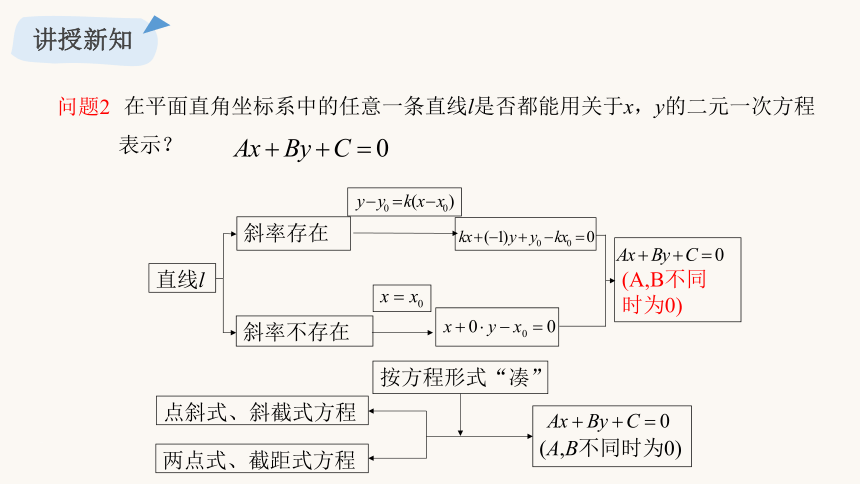
问题2
在平面直角坐标系中的任意一条直线l是否都能用关于x,y的二元一次方程 表示?
斜率存在
斜率不存在
直线l
(A,B不同时为0)
(A,B不同时为0)
点斜式、斜截式方程
两点式、截距式方程
按方程形式“凑”
(A,B不同时为0)
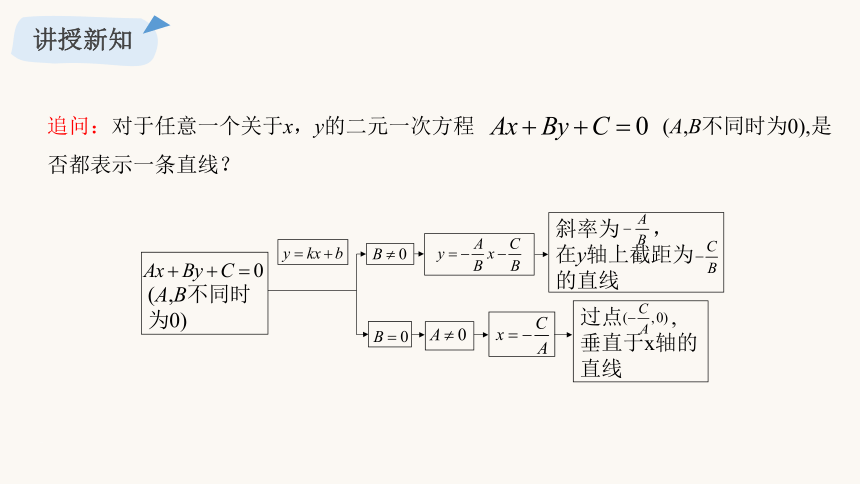
斜率为 ,
在y轴上截距为 的直线
过点 ,
垂直于x轴的直线
追问:对于任意一个关于x,y的二元一次方程 (A,B不同时为0),是否都表示一条直线?
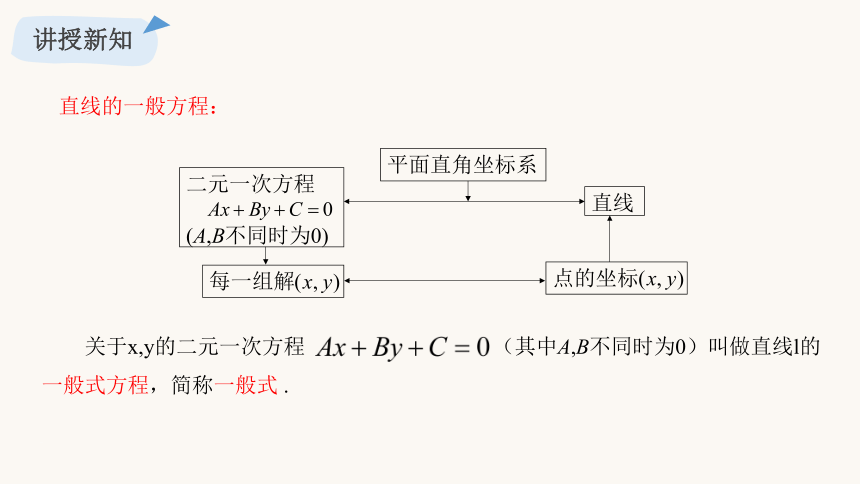
二元一次方程
(A,B不同时为0)
直线
平面直角坐标系
每一组解
点的坐标
关于x,y的二元一次方程 (其中A,B不同时为0)叫做直线l的一般式方程,简称一般式 .
直线的一般方程:
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(1)平行于x轴?
不同时为0
斜率为0,
在y轴截距不为0
平行于x轴
,
x
y
O
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(2)平行于y轴?
x
y
O
不同时为0
斜率不存在,
在x轴截距不为0
平行于y轴
,
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(3)与x轴重合?
x
y
O
不同时为0
斜率为0,
在y轴截距为0
与x轴重合
,
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(4)与y轴重合?
x
y
O
不同时为0
斜率不存在,
在x轴截距为0
与y轴重合
,
问题4 你能总结直线五种形式的方程之间有什么关系以及各自的适用范围吗?
斜率存在
与坐标轴垂直,过原点
与坐标轴垂直
例题讲解
直线的点斜式方程
直线上的一点
直线的斜率
直线的一般式方程
例1 已知直线经过点 , 斜率为 ,求直线的点斜式、一般式方程.
解:经过点 ,斜率为 的直线的点斜式方程为:
,
化为一般式,得: .
整理得:
例题讲解
例2 把直线l的一般式方程 化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
直线的
斜截式方程
直线的
一般式方程
直线斜率
时, x的值
直线在y轴上截距
直线在x轴上截距
直线与x轴
交点横坐标
直线与两坐标轴的交点
经过两点绘制直线
例题讲解
例2 把直线l的一般式方程 化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
解:把直线l的一般式方程化为斜截式: .
因此,直线l的斜率 ,它在y轴上的截距是3.
在直线l的方程 中,令 y=0,得 ,
即直线在x轴上的截距是-6.
则直线l与x轴、y轴的交点分别为A(6,0),B(0,3),
过A,B两点作直线,就得直线l(如图).
练一练
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点,斜率是,
(2)经过点平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
练一练
2.已知直线的方程是Ax+By+C=0.
(1)当B≠0时,直线的斜率是多少?当B=0时呢?
(2)系数取什么值时,方程表示经过原点的直线?
本节课你学到了哪些知识与方法?
2.2.3 直线的一般方程
1.了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系.(重点)
2.能正确地进行直线的一般式方程与特殊形式的方程的转化.(重点)
3.能运用直线的一般式方程解决有关问题.(难点)
复习导入
想一想:我们前面学习的直线方程中都有几个变量
这些方程的共同特征是什么
直线的方程
一点及斜率
直线上两点
点斜式
斜截式
两点式
截距式
直线的方程
点斜式
斜截式
两点式
截距式
问题1
四种表示直线的方程,它们有怎样的区别与联系?
联系:
直线上任意点的几何特征
直线的代数表示:直线上点的横纵坐标x,y的关系
区别:应用条件不同;表达形式不同;
追问1.1:以上四种方程在表示直线时有怎样的局限性?
×
×
×
×
×
×
×
√
√
√
√
√
问题2
在平面直角坐标系中的任意一条直线l是否都能用关于x,y的二元一次方程 表示?
斜率存在
斜率不存在
直线l
(A,B不同时为0)
(A,B不同时为0)
点斜式、斜截式方程
两点式、截距式方程
按方程形式“凑”
(A,B不同时为0)
斜率为 ,
在y轴上截距为 的直线
过点 ,
垂直于x轴的直线
追问:对于任意一个关于x,y的二元一次方程 (A,B不同时为0),是否都表示一条直线?
二元一次方程
(A,B不同时为0)
直线
平面直角坐标系
每一组解
点的坐标
关于x,y的二元一次方程 (其中A,B不同时为0)叫做直线l的一般式方程,简称一般式 .
直线的一般方程:
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(1)平行于x轴?
不同时为0
斜率为0,
在y轴截距不为0
平行于x轴
,
x
y
O
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(2)平行于y轴?
x
y
O
不同时为0
斜率不存在,
在x轴截距不为0
平行于y轴
,
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(3)与x轴重合?
x
y
O
不同时为0
斜率为0,
在y轴截距为0
与x轴重合
,
(1)平行于x轴?(2)平行于y轴?
(3)与x轴重合?(4)与y轴重合?
问题3
在方程 中, 为何值时,方程表示如下直线:
(4)与y轴重合?
x
y
O
不同时为0
斜率不存在,
在x轴截距为0
与y轴重合
,
问题4 你能总结直线五种形式的方程之间有什么关系以及各自的适用范围吗?
斜率存在
与坐标轴垂直,过原点
与坐标轴垂直
例题讲解
直线的点斜式方程
直线上的一点
直线的斜率
直线的一般式方程
例1 已知直线经过点 , 斜率为 ,求直线的点斜式、一般式方程.
解:经过点 ,斜率为 的直线的点斜式方程为:
,
化为一般式,得: .
整理得:
例题讲解
例2 把直线l的一般式方程 化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
直线的
斜截式方程
直线的
一般式方程
直线斜率
时, x的值
直线在y轴上截距
直线在x轴上截距
直线与x轴
交点横坐标
直线与两坐标轴的交点
经过两点绘制直线
例题讲解
例2 把直线l的一般式方程 化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
解:把直线l的一般式方程化为斜截式: .
因此,直线l的斜率 ,它在y轴上的截距是3.
在直线l的方程 中,令 y=0,得 ,
即直线在x轴上的截距是-6.
则直线l与x轴、y轴的交点分别为A(6,0),B(0,3),
过A,B两点作直线,就得直线l(如图).
练一练
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点,斜率是,
(2)经过点平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
练一练
2.已知直线的方程是Ax+By+C=0.
(1)当B≠0时,直线的斜率是多少?当B=0时呢?
(2)系数取什么值时,方程表示经过原点的直线?
本节课你学到了哪些知识与方法?
