2.3.1 两条直线的交点坐标 课件(共15张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.3.1 两条直线的交点坐标 课件(共15张PPT) 2024~2025学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 438.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.3.1 两条直线的交点坐标
学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.会根据方程解的个数判定两条直线的位置关系.
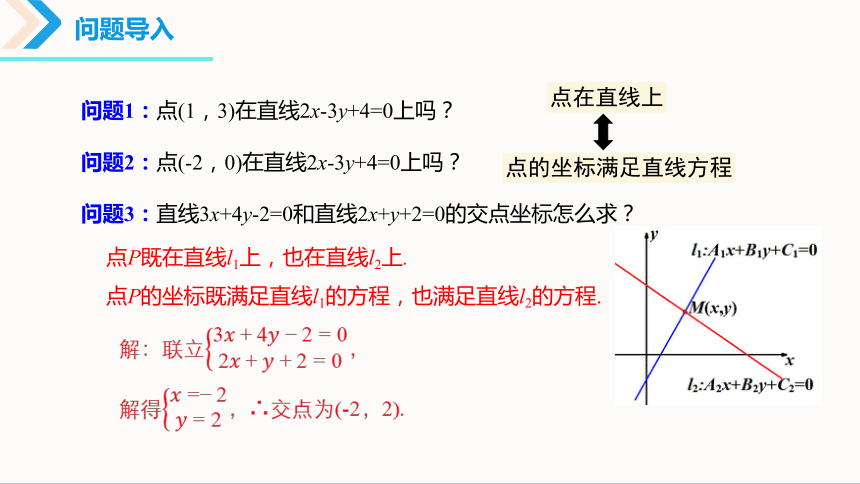
问题导入
问题1:点(1,3)在直线2x-3y+4=0上吗?
问题2:点(-2,0)在直线2x-3y+4=0上吗?
问题3:直线3x+4y-2=0和直线2x+y+2=0的交点坐标怎么求?
点P既在直线l1上,也在直线l2上.
点P的坐标既满足直线l1的方程,也满足直线l2的方程.
解:联立,
解得,∴交点为(-2,2).
新课讲授
已知两条直线的方程是l1:A1x+B1y+C1=0, l2:A2x+B2y+C2=0,设这
两条直线的交点为P,则点P的坐标就是方程组 的解.
(1)求交点坐标:
概念讲解
方程组的解 唯一解 无数个解 无解
直线l1和l2交点个数 1个 无数个 0个
直线l1和l2的位置关系 相交 重合 平行
(2)交点个数与直线位置关系:
例1 判断下列各对直线的位置关系.如果相交,求出交点的坐标:
(1)l1:x-y=0,l2:3x+3y-10=0;
(2)l1:3x-y+4=0,l2:6x-2y-1=0;
(3)l1:3x+4y-5=0,l2:6x+8y-10=0.
解:(1)解方程组得,
∴l1与l2相交,交点为(,),
(2)解方程组,
×2-得9=0,矛盾,这个方程组无解,
∴l1与l2无公共点,l1∥l2.
例1 判断下列各对直线的位置关系.如果相交,求出交点的坐标:
(3)l1:3x+4y-5=0,l2:6x+8y-10=0.
(3)解方程组,
×2得6x+8y-10=0,
和可化成同一个方程,
即和表示同一条直线,l1与l2重合.
判断两条直线位置关系的方法
归纳总结
练1.分别判断下列直线是否相交,若相交,求出交点坐标.
(1)l1:2x-y=7和l2:3x+2y-7=0;
(2)l1:2x-6y+4=0和l2:4x-12y+8=0;
(3)l1:4x+2y+4=0和l2:y=-2x+3.
解:(1)相交,交点坐标为(3,-1).
(2)重合.
(3)平行.
问题4:观察下面的图象,发现直线都经过点M(4,1),怎么表示出经过M点的直线方程?
当斜率存在时,y-1=k(x-4)(k∈R);当斜率不存在时,x=4.
例2 无论m为何值,直线l:(m+1)x-y-7m-4=0恒过一定点P,求点P的坐标.
解:∵(m+1)x-y-7m-4=0,
∴m(x-7)+(x-y-4)=0,
∴,
∴,
∴点P的坐标为(7,3).
练2.已知直线l:(2a+3)x-(a-1)y +3a+7=0,a∈R.直线l过定点A,求出点A的坐标.
解:由题可得,(2x-y+3)a+3x+y+7=0,
∴直线l过直线2x-y+3=0与3x+y+7=0的交点,
解方程组得,
∴直线l过定点A,点A的坐标为(-2,-1).
例3 (1)求经过点(2,3)且经过直线l1:x+3y-4=0与l2:5x+2y+6=0的交点的直线方程;
(2)求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0垂直的直线方程.
解:(1)联立,
解得,
∴直线l1与l2的交点为(-2,2),
由两点式可得所求直线方程为,即x-4y+10=0.
(2)由方程组得,
∵所求直线和直线3x+y-1=0垂直,∴所求直线的斜率k=,
∴有,
即所求直线方程为5x-15y-18=0.
(2)求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0垂直的直线方程.
课堂总结
(1)两条直线的交点.
(2)两条直线的位置关系
(3)直线过定点问题.
当堂检测
1.两条直线l1:2x-y-1=0与l2:x+3y-11=0的交点坐标为( )
A.(3,2) B.(2,3)
C.(-2,-3) D.(-3,-2)
2.不论m为何实数,直线l:(m-1)x+(2m-3)y+m=0恒过定点( )
A.(-3,-1) B.(-2,-1)
C.(-3,1) D.(-2,1)
3.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则点P的坐标为 .
B
C
(3,3)
2.3.1 两条直线的交点坐标
学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.会根据方程解的个数判定两条直线的位置关系.
问题导入
问题1:点(1,3)在直线2x-3y+4=0上吗?
问题2:点(-2,0)在直线2x-3y+4=0上吗?
问题3:直线3x+4y-2=0和直线2x+y+2=0的交点坐标怎么求?
点P既在直线l1上,也在直线l2上.
点P的坐标既满足直线l1的方程,也满足直线l2的方程.
解:联立,
解得,∴交点为(-2,2).
新课讲授
已知两条直线的方程是l1:A1x+B1y+C1=0, l2:A2x+B2y+C2=0,设这
两条直线的交点为P,则点P的坐标就是方程组 的解.
(1)求交点坐标:
概念讲解
方程组的解 唯一解 无数个解 无解
直线l1和l2交点个数 1个 无数个 0个
直线l1和l2的位置关系 相交 重合 平行
(2)交点个数与直线位置关系:
例1 判断下列各对直线的位置关系.如果相交,求出交点的坐标:
(1)l1:x-y=0,l2:3x+3y-10=0;
(2)l1:3x-y+4=0,l2:6x-2y-1=0;
(3)l1:3x+4y-5=0,l2:6x+8y-10=0.
解:(1)解方程组得,
∴l1与l2相交,交点为(,),
(2)解方程组,
×2-得9=0,矛盾,这个方程组无解,
∴l1与l2无公共点,l1∥l2.
例1 判断下列各对直线的位置关系.如果相交,求出交点的坐标:
(3)l1:3x+4y-5=0,l2:6x+8y-10=0.
(3)解方程组,
×2得6x+8y-10=0,
和可化成同一个方程,
即和表示同一条直线,l1与l2重合.
判断两条直线位置关系的方法
归纳总结
练1.分别判断下列直线是否相交,若相交,求出交点坐标.
(1)l1:2x-y=7和l2:3x+2y-7=0;
(2)l1:2x-6y+4=0和l2:4x-12y+8=0;
(3)l1:4x+2y+4=0和l2:y=-2x+3.
解:(1)相交,交点坐标为(3,-1).
(2)重合.
(3)平行.
问题4:观察下面的图象,发现直线都经过点M(4,1),怎么表示出经过M点的直线方程?
当斜率存在时,y-1=k(x-4)(k∈R);当斜率不存在时,x=4.
例2 无论m为何值,直线l:(m+1)x-y-7m-4=0恒过一定点P,求点P的坐标.
解:∵(m+1)x-y-7m-4=0,
∴m(x-7)+(x-y-4)=0,
∴,
∴,
∴点P的坐标为(7,3).
练2.已知直线l:(2a+3)x-(a-1)y +3a+7=0,a∈R.直线l过定点A,求出点A的坐标.
解:由题可得,(2x-y+3)a+3x+y+7=0,
∴直线l过直线2x-y+3=0与3x+y+7=0的交点,
解方程组得,
∴直线l过定点A,点A的坐标为(-2,-1).
例3 (1)求经过点(2,3)且经过直线l1:x+3y-4=0与l2:5x+2y+6=0的交点的直线方程;
(2)求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0垂直的直线方程.
解:(1)联立,
解得,
∴直线l1与l2的交点为(-2,2),
由两点式可得所求直线方程为,即x-4y+10=0.
(2)由方程组得,
∵所求直线和直线3x+y-1=0垂直,∴所求直线的斜率k=,
∴有,
即所求直线方程为5x-15y-18=0.
(2)求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0垂直的直线方程.
课堂总结
(1)两条直线的交点.
(2)两条直线的位置关系
(3)直线过定点问题.
当堂检测
1.两条直线l1:2x-y-1=0与l2:x+3y-11=0的交点坐标为( )
A.(3,2) B.(2,3)
C.(-2,-3) D.(-3,-2)
2.不论m为何实数,直线l:(m-1)x+(2m-3)y+m=0恒过定点( )
A.(-3,-1) B.(-2,-1)
C.(-3,1) D.(-2,1)
3.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则点P的坐标为 .
B
C
(3,3)
