湖南省澧县张公庙中学2015-2016学年第二学期九年级入学考试数学试卷
文档属性
| 名称 | 湖南省澧县张公庙中学2015-2016学年第二学期九年级入学考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-02 08:17:41 | ||
图片预览


文档简介
湖南省澧县张公庙中学2015-2016学年第二学期九年级入学考试数学试卷
一.选择题(共8小题)
1.若关于x的方程x2+3x+a=0有一个根为﹣1,则另一个根为( )
A.﹣2 B.2 C.4 D.﹣3
2.若一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数y=的图象在( )
A.一、三象限 B.二、四象限 C.一、二象限 D.三、四象限
3.已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
A.﹣1<x<3 B.﹣1<x<4 C.x<﹣1或x>3 D.x<﹣1或x>4
4.两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
A.8和12 B.9和11 C.7和13 D.6和14
5.下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4 B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6 D.a=2,b=3,c=4,d=1
6.在三角形ABC中,∠C为直角,sinA=,则tanB的值为( )
A. B. C. D.
7.如图,将△ABC放在每个小正方形边长 ( http: / / www.21cnjy.com )为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C.2 D.
8.丽华根据演讲比赛中九位评委所给的分数作了如下表格
平均数 中位数 众数 方差
8.5 8.3 8.1 0.15
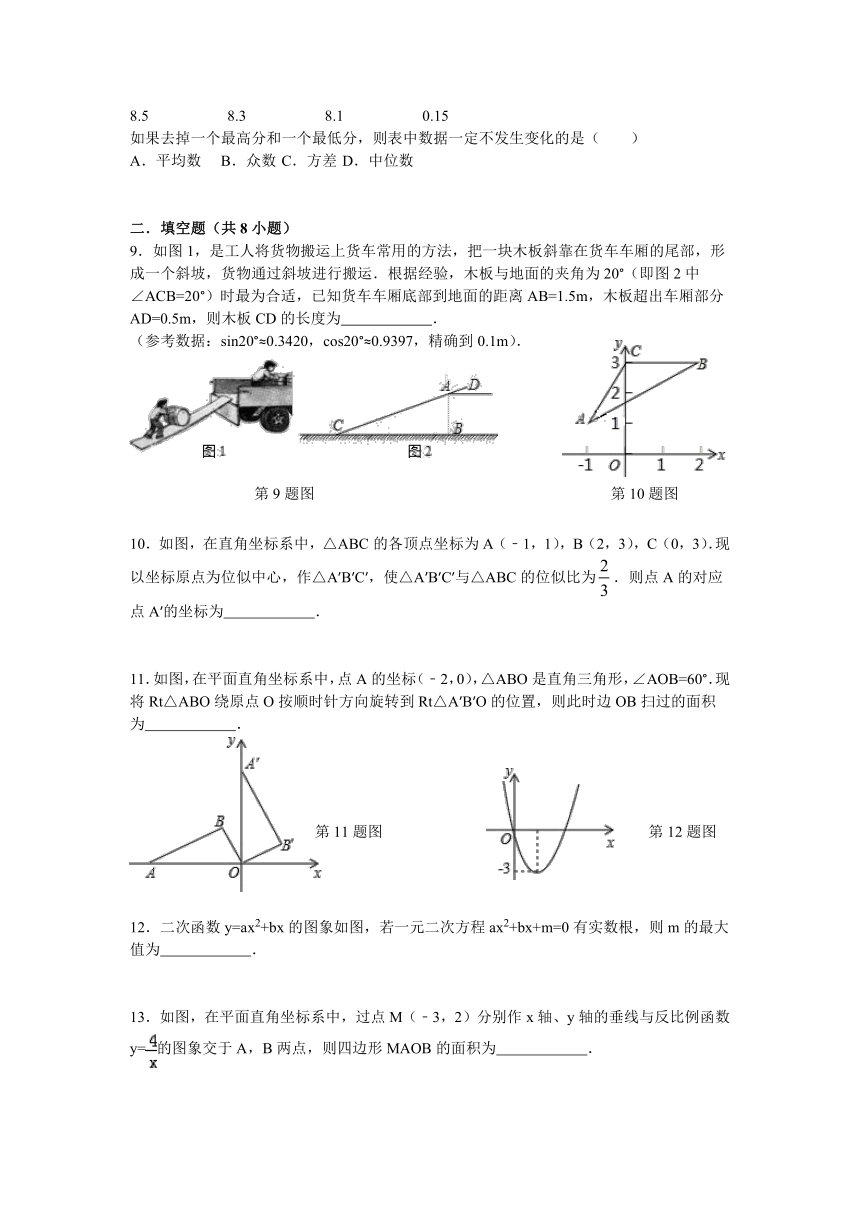
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数 B.众数 C.方差 D.中位数
二.填空题(共8小题)
9.如图1,是工人将货物搬运上货车常用的方 ( http: / / www.21cnjy.com )法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为 .
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
( http: / / www.21cnjy.com )
10.如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为.则点A的对应点A′的坐标为 .
11.如图,在平面直角坐标系中,点A的坐标 ( http: / / www.21cnjy.com )(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为 .
12.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .
13.如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=的图象交于A,B两点,则四边形MAOB的面积为 .
14.小明设计了一个魔术盒 ( http: / / www.21cnjy.com ),当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3.若将实数(x,﹣2x)放入其中,得到﹣1,则x= .
15.如图,PA,PB是⊙O的两条切线 ( http: / / www.21cnjy.com ),切点分别是A、B,PA=10,CD是⊙O的切线,交PA于点C,交PB于点D,则△PCD的周长是 .
16.如图,已知点A1,A2,…, ( http: / / www.21cnjy.com )A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
( http: / / www.21cnjy.com )
三.解答题(共9小题)
17.用公式法解下列方程2x2+6=7x.
18.计算:sin45°+cos230°﹣+2sin60°.
19.如图,△ABC是直角三角形,∠ACB=90°.
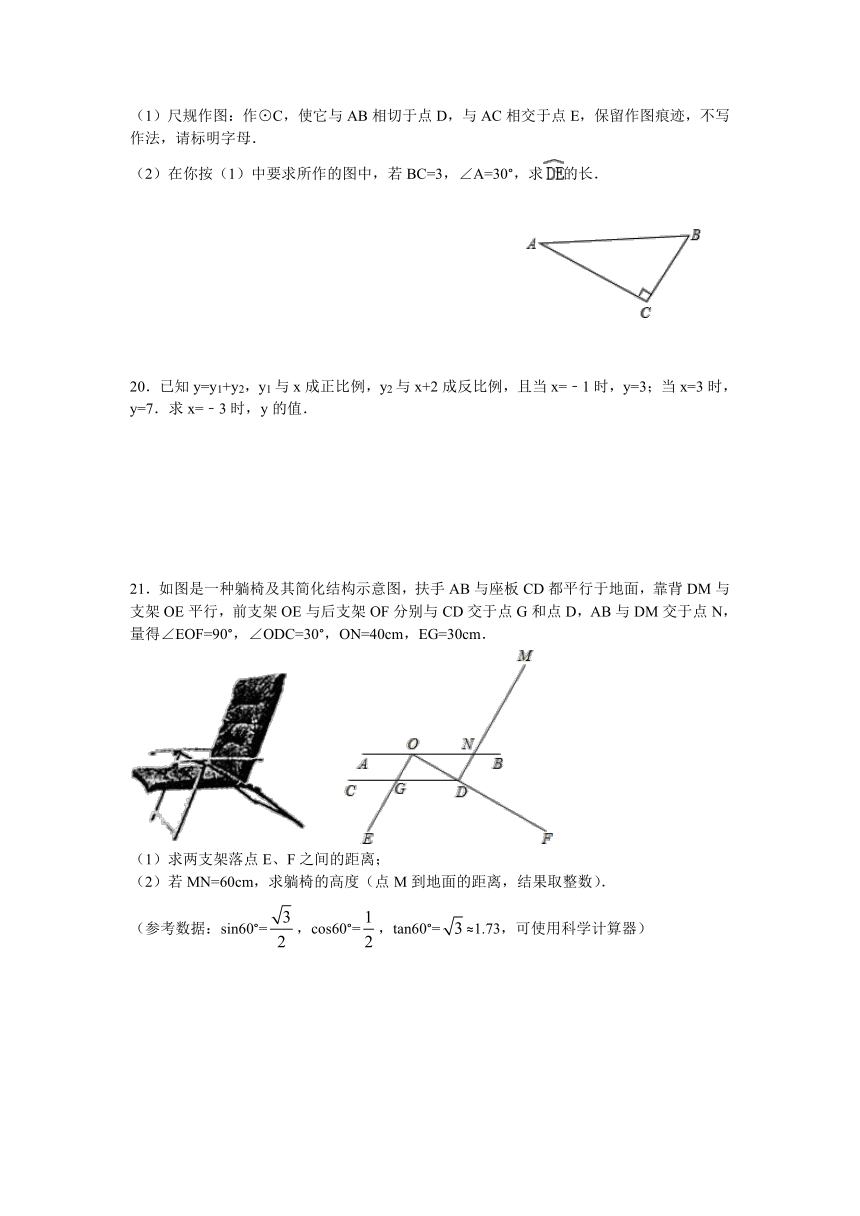
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.
20.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
21.如图是一种躺椅及其简化结构示意图,扶手AB与座板CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,量得∠EOF=90°,∠ODC=30°,ON=40cm,EG=30cm. ( http: / / www.21cnjy.com )
(1)求两支架落点E、F之间的距离;
(2)若MN=60cm,求躺椅的高度(点M到地面的距离,结果取整数).
(参考数据:sin60°=,cos60°=,tan60°=≈1.73,可使用科学计算器)
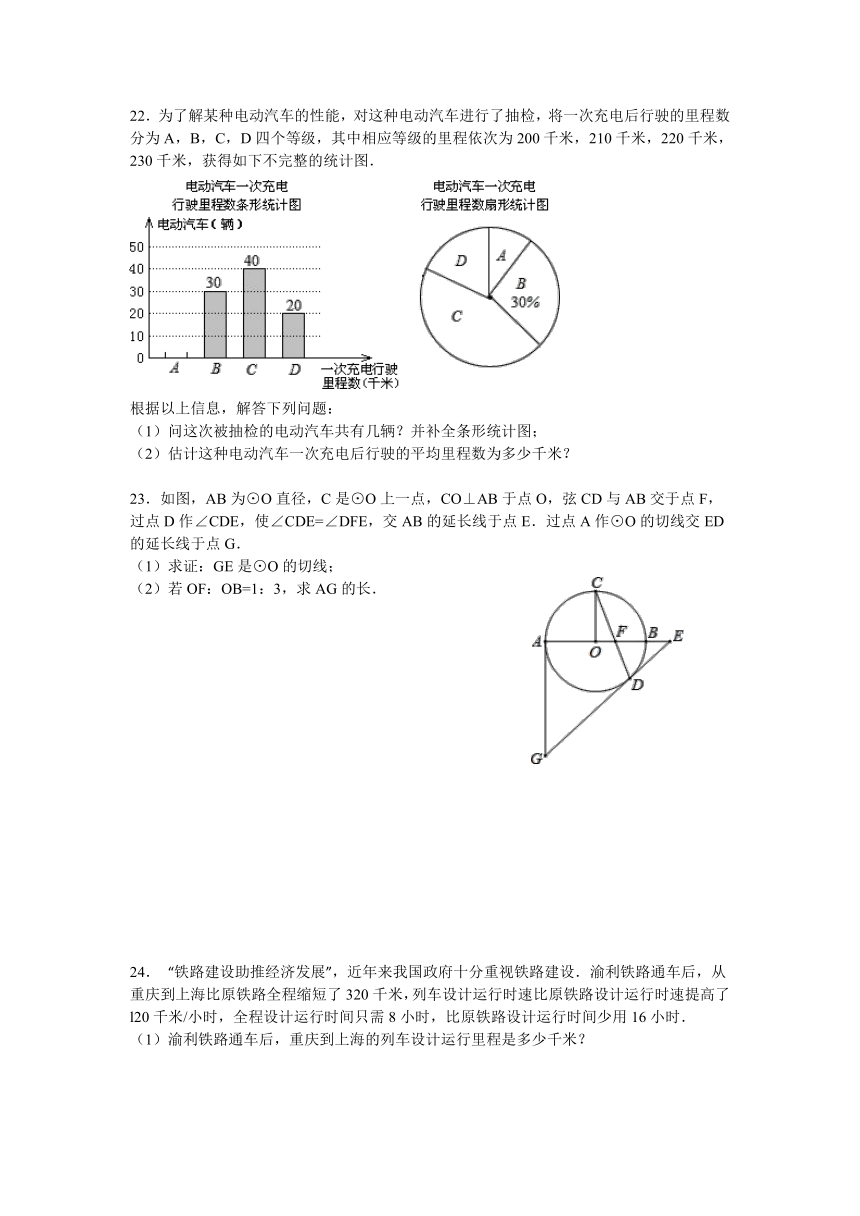
22.为了解某种电动汽车的性能,对 ( http: / / www.21cnjy.com )这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.
( http: / / www.21cnjy.com )
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
23.如图,AB为⊙O直径,C是⊙O上一点, ( http: / / www.21cnjy.com )CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.
(1)求证:GE是⊙O的切线;
(2)若OF:OB=1:3,求AG的长.
24. “铁路建设助推经济 ( http: / / www.21cnjy.com )发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了l20千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加m小时,求m的值.
25.在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=AD,点N是折线AB﹣BC上的一个动点.
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求的值.
( http: / / www.21cnjy.com )
26. 如图,已知二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
( http: / / www.21cnjy.com )
湖南省澧县张公庙中学2015-2016学年第二学期九年级入学考试数学试卷
参考答案
一.选择题(共8小题)
1. A. 2. A. 3. C. 4. A. 5. C. 6. C. 7. A. 8. D.
二.填空题(共8小题)
9. 4.9m . 10. (﹣,)或(,﹣) . 11. π .
12. 3 . 13. 10 . 14. ﹣2 . 15. 20 . 16. 2011 .
三.解答题(共10小题)
17. x1=2,x2=. 18.1+.
19.解:(1)如图,
⊙C为所求;
(2)∵⊙C切AB于D,
∴CD⊥AB,
∴∠ADC=90°,
∴∠DCE=90°﹣∠A=90°﹣30°=60°,
∴∠BCD=90°﹣∠ACD=30°,
在Rt△BCD中,∵cos∠BCD=,
∴CD=3cos30°=,
∴的长==π.
20.解:∵y1与x成正比例,
∴y1=kx,
∵y2与x+2成反比例,
∴y2=,
∵y=y1+y2,
∴y=kx+,
∵当x=﹣1时,y=3;当x=3时,y=7,
∴,
解得:,
∴y=2x+,
当x=﹣3时,y=2×(﹣3)﹣5=﹣11.
21.解:(1)连接EF.
∵CD平行于地面,
∴GD∥EF.
∴.
又∵AB∥EF,
∴AB∥CD.
而OE∥DM,
则四边形OGDN是平行四边形.
∴OG=DN,GD=ON.
∵ON=40cm,∠EOF=90°,∠ODC=30°,
∴GD=40cm,OG=GD=20cm,又EG=30cm,
即,得EF=100cm.
(2)延长MD交EF于点H,过点M作MP⊥EF于点P.
∵四边形ONHE是平行四边形,
∴NH=OE=50cm,∠MHF=∠E=60°.
由于MN=60cm,∴MH=110cm.
在Rt△MHP中,MP=MH sin∠MHP,
即MP=110sin60°=110×=55≈95(cm).
答:躺椅的高度约为95cm.
22.解:(1)这次被抽检的电动汽车共有:30÷30%=100(辆),
C所占的百分比为:40÷100×100%=40%,D所占的百分比为:20÷100×100%=20%,
A所占的百分比为:100%﹣40%﹣20%﹣30%=10%,
A等级电动汽车的辆数为:100×10%=10(辆),
补全统计图如图所示:
( http: / / www.21cnjy.com )
(2)这种电动汽车一次充电后行驶的平均里程数为:230)=217(千米),
∴估计这种电动汽车一次充电后行驶的平均里程数为217千米.
23.(1)证明:连接OD.
∵OC=OD,
∴∠C=∠ODC,
∵OC⊥AB,
∴∠COF=90°
∴∠OCD+∠CFO=90°,
∴∠ODC+∠CFO=90°,
∵∠EFD=∠FDE,
∠EFD=∠CDE,
∴∠CDO+∠CDE=90°,
∴DE为⊙O的切线;
(2)解:∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,
∵∠EFD=∠EDF,
∴EF=ED,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=EO2,
∴32+x2=(x+1)2,
解得:x=4,
∴DE=4,OE=5,
∵AG为⊙O的切线,
∴AG⊥AE,
∴∠GAE=90°,
∵∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴==,
即=,
解得:AG=6.
24.解:(1)设原时速为xkm/h,通车后里程为ykm,则有:
解得:,
答:渝利铁路通车后,重庆到上海的列车设计运行里程是1600千米;
(2)由题意可得出:(80+120)(1﹣m%)(8+m)=1600,
解得:m1=20,m2=0(不合题意舍去),
答:m的值为20.
25.(1).
(2)① 1 ;
解:(1)如图1,过点N作NG⊥AB于G,
∵四边形ABCD是菱形,
∴AD∥BC,OD=OB,
∴==1,
∴BN=DM=AD=1,
∵∠DAB=60°,
∴∠NBG=60°
∴BG=,GN=,
∴AN===;
故答案为:;
(2)①当点A′落在AB边上,则MN为AA′的中垂线,
∵∠DAB=60°AM=2,
∴AN=AM=1,
故答案为:1;
②在菱形ABCD中,AC平分∠DAB,
∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵△AMN沿MN翻折得到△A′MN,
∴AC⊥MN,AM=A′M,AN=A′N,
∴∠AMN=∠ANM=60°,
∴AM=AN,
∴AM=A′M=AN=A′N,
∴四边形AM A′N是菱形;
③在菱形ABCD中,AB=AD,
∴∠ADB=∠ABD=60°,
∴∠BA′M=∠DMA′+∠ADB,
∴A′M=AM=2,∠NA′M=∠A=60°,
∴∠NA′B=∠DMA′,
∴△DMA′∽△BA′N,
∴=,
∵MD=AD=1,A′M=2,
∴=.
26. 解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴,
解得.
∴抛物线表达式:y=﹣x2+x+4;
(2)△ABC是直角三角形.
令y=0,则﹣x2+x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC==4,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)
③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,
∴MD∥OA,
∴△BMD∽△BAO,
∴=,
∵MN∥AC
∴=,
∴=,
∵OA=4,BC=10,BN=n+2
∴MD=(n+2),
∵S△AMN=S△ABN﹣S△BMN
=BN OA﹣BN MD
=(n+2)×4﹣×(n+2)2
=﹣(n﹣3)2+5,
∴当△AMN面积最大时,N点坐标为(3,0).
第3题图
第7题图
第10题图
第9题图
第12题图
第11题图
第15题图
第13题图
一.选择题(共8小题)
1.若关于x的方程x2+3x+a=0有一个根为﹣1,则另一个根为( )
A.﹣2 B.2 C.4 D.﹣3
2.若一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数y=的图象在( )
A.一、三象限 B.二、四象限 C.一、二象限 D.三、四象限
3.已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
A.﹣1<x<3 B.﹣1<x<4 C.x<﹣1或x>3 D.x<﹣1或x>4
4.两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
A.8和12 B.9和11 C.7和13 D.6和14
5.下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4 B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6 D.a=2,b=3,c=4,d=1
6.在三角形ABC中,∠C为直角,sinA=,则tanB的值为( )
A. B. C. D.
7.如图,将△ABC放在每个小正方形边长 ( http: / / www.21cnjy.com )为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C.2 D.
8.丽华根据演讲比赛中九位评委所给的分数作了如下表格
平均数 中位数 众数 方差
8.5 8.3 8.1 0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数 B.众数 C.方差 D.中位数
二.填空题(共8小题)
9.如图1,是工人将货物搬运上货车常用的方 ( http: / / www.21cnjy.com )法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为 .
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
( http: / / www.21cnjy.com )
10.如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为.则点A的对应点A′的坐标为 .
11.如图,在平面直角坐标系中,点A的坐标 ( http: / / www.21cnjy.com )(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为 .
12.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .
13.如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=的图象交于A,B两点,则四边形MAOB的面积为 .
14.小明设计了一个魔术盒 ( http: / / www.21cnjy.com ),当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3.若将实数(x,﹣2x)放入其中,得到﹣1,则x= .
15.如图,PA,PB是⊙O的两条切线 ( http: / / www.21cnjy.com ),切点分别是A、B,PA=10,CD是⊙O的切线,交PA于点C,交PB于点D,则△PCD的周长是 .
16.如图,已知点A1,A2,…, ( http: / / www.21cnjy.com )A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
( http: / / www.21cnjy.com )
三.解答题(共9小题)
17.用公式法解下列方程2x2+6=7x.
18.计算:sin45°+cos230°﹣+2sin60°.
19.如图,△ABC是直角三角形,∠ACB=90°.
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.
20.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
21.如图是一种躺椅及其简化结构示意图,扶手AB与座板CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,量得∠EOF=90°,∠ODC=30°,ON=40cm,EG=30cm. ( http: / / www.21cnjy.com )
(1)求两支架落点E、F之间的距离;
(2)若MN=60cm,求躺椅的高度(点M到地面的距离,结果取整数).
(参考数据:sin60°=,cos60°=,tan60°=≈1.73,可使用科学计算器)
22.为了解某种电动汽车的性能,对 ( http: / / www.21cnjy.com )这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.
( http: / / www.21cnjy.com )
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
23.如图,AB为⊙O直径,C是⊙O上一点, ( http: / / www.21cnjy.com )CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.
(1)求证:GE是⊙O的切线;
(2)若OF:OB=1:3,求AG的长.
24. “铁路建设助推经济 ( http: / / www.21cnjy.com )发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了l20千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加m小时,求m的值.
25.在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=AD,点N是折线AB﹣BC上的一个动点.
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求的值.
( http: / / www.21cnjy.com )
26. 如图,已知二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
( http: / / www.21cnjy.com )
湖南省澧县张公庙中学2015-2016学年第二学期九年级入学考试数学试卷
参考答案
一.选择题(共8小题)
1. A. 2. A. 3. C. 4. A. 5. C. 6. C. 7. A. 8. D.
二.填空题(共8小题)
9. 4.9m . 10. (﹣,)或(,﹣) . 11. π .
12. 3 . 13. 10 . 14. ﹣2 . 15. 20 . 16. 2011 .
三.解答题(共10小题)
17. x1=2,x2=. 18.1+.
19.解:(1)如图,
⊙C为所求;
(2)∵⊙C切AB于D,
∴CD⊥AB,
∴∠ADC=90°,
∴∠DCE=90°﹣∠A=90°﹣30°=60°,
∴∠BCD=90°﹣∠ACD=30°,
在Rt△BCD中,∵cos∠BCD=,
∴CD=3cos30°=,
∴的长==π.
20.解:∵y1与x成正比例,
∴y1=kx,
∵y2与x+2成反比例,
∴y2=,
∵y=y1+y2,
∴y=kx+,
∵当x=﹣1时,y=3;当x=3时,y=7,
∴,
解得:,
∴y=2x+,
当x=﹣3时,y=2×(﹣3)﹣5=﹣11.
21.解:(1)连接EF.
∵CD平行于地面,
∴GD∥EF.
∴.
又∵AB∥EF,
∴AB∥CD.
而OE∥DM,
则四边形OGDN是平行四边形.
∴OG=DN,GD=ON.
∵ON=40cm,∠EOF=90°,∠ODC=30°,
∴GD=40cm,OG=GD=20cm,又EG=30cm,
即,得EF=100cm.
(2)延长MD交EF于点H,过点M作MP⊥EF于点P.
∵四边形ONHE是平行四边形,
∴NH=OE=50cm,∠MHF=∠E=60°.
由于MN=60cm,∴MH=110cm.
在Rt△MHP中,MP=MH sin∠MHP,
即MP=110sin60°=110×=55≈95(cm).
答:躺椅的高度约为95cm.
22.解:(1)这次被抽检的电动汽车共有:30÷30%=100(辆),
C所占的百分比为:40÷100×100%=40%,D所占的百分比为:20÷100×100%=20%,
A所占的百分比为:100%﹣40%﹣20%﹣30%=10%,
A等级电动汽车的辆数为:100×10%=10(辆),
补全统计图如图所示:
( http: / / www.21cnjy.com )
(2)这种电动汽车一次充电后行驶的平均里程数为:230)=217(千米),
∴估计这种电动汽车一次充电后行驶的平均里程数为217千米.
23.(1)证明:连接OD.
∵OC=OD,
∴∠C=∠ODC,
∵OC⊥AB,
∴∠COF=90°
∴∠OCD+∠CFO=90°,
∴∠ODC+∠CFO=90°,
∵∠EFD=∠FDE,
∠EFD=∠CDE,
∴∠CDO+∠CDE=90°,
∴DE为⊙O的切线;
(2)解:∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,
∵∠EFD=∠EDF,
∴EF=ED,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=EO2,
∴32+x2=(x+1)2,
解得:x=4,
∴DE=4,OE=5,
∵AG为⊙O的切线,
∴AG⊥AE,
∴∠GAE=90°,
∵∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴==,
即=,
解得:AG=6.
24.解:(1)设原时速为xkm/h,通车后里程为ykm,则有:
解得:,
答:渝利铁路通车后,重庆到上海的列车设计运行里程是1600千米;
(2)由题意可得出:(80+120)(1﹣m%)(8+m)=1600,
解得:m1=20,m2=0(不合题意舍去),
答:m的值为20.
25.(1).
(2)① 1 ;
解:(1)如图1,过点N作NG⊥AB于G,
∵四边形ABCD是菱形,
∴AD∥BC,OD=OB,
∴==1,
∴BN=DM=AD=1,
∵∠DAB=60°,
∴∠NBG=60°
∴BG=,GN=,
∴AN===;
故答案为:;
(2)①当点A′落在AB边上,则MN为AA′的中垂线,
∵∠DAB=60°AM=2,
∴AN=AM=1,
故答案为:1;
②在菱形ABCD中,AC平分∠DAB,
∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵△AMN沿MN翻折得到△A′MN,
∴AC⊥MN,AM=A′M,AN=A′N,
∴∠AMN=∠ANM=60°,
∴AM=AN,
∴AM=A′M=AN=A′N,
∴四边形AM A′N是菱形;
③在菱形ABCD中,AB=AD,
∴∠ADB=∠ABD=60°,
∴∠BA′M=∠DMA′+∠ADB,
∴A′M=AM=2,∠NA′M=∠A=60°,
∴∠NA′B=∠DMA′,
∴△DMA′∽△BA′N,
∴=,
∵MD=AD=1,A′M=2,
∴=.
26. 解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴,
解得.
∴抛物线表达式:y=﹣x2+x+4;
(2)△ABC是直角三角形.
令y=0,则﹣x2+x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC==4,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)
③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,
∴MD∥OA,
∴△BMD∽△BAO,
∴=,
∵MN∥AC
∴=,
∴=,
∵OA=4,BC=10,BN=n+2
∴MD=(n+2),
∵S△AMN=S△ABN﹣S△BMN
=BN OA﹣BN MD
=(n+2)×4﹣×(n+2)2
=﹣(n﹣3)2+5,
∴当△AMN面积最大时,N点坐标为(3,0).
第3题图
第7题图
第10题图
第9题图
第12题图
第11题图
第15题图
第13题图
同课章节目录
