沪科版九年级下册24.5三角形的内切圆 课件(16张PPT)
文档属性
| 名称 | 沪科版九年级下册24.5三角形的内切圆 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-02 11:28:53 | ||
图片预览


文档简介
课件16张PPT。24.5 三角形的内切圆1. 确定圆的条件是什么?1)圆心与半径2. 叙述角平分线的性质定理与判定定理性质:角平分线上的点到这个角的两边的距离相等。
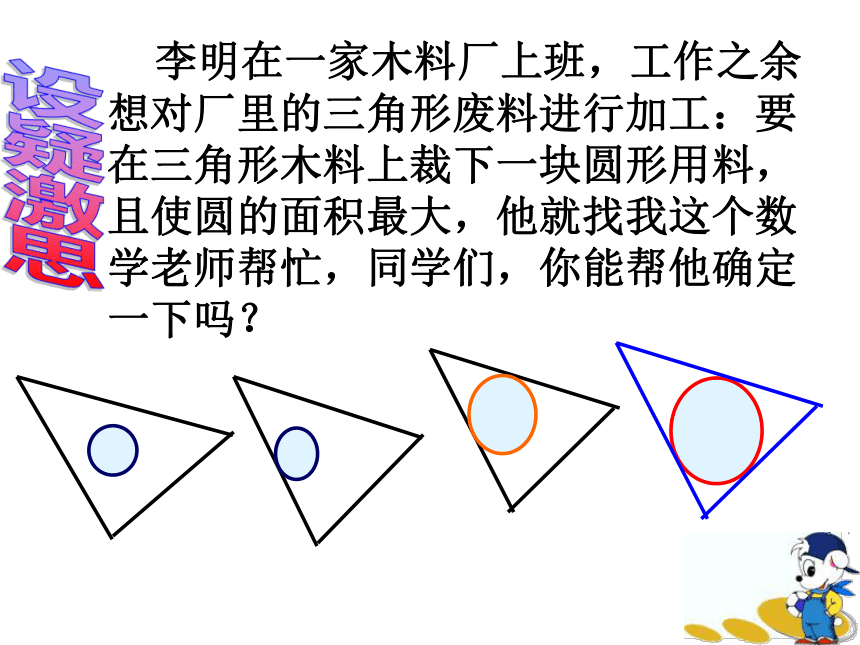
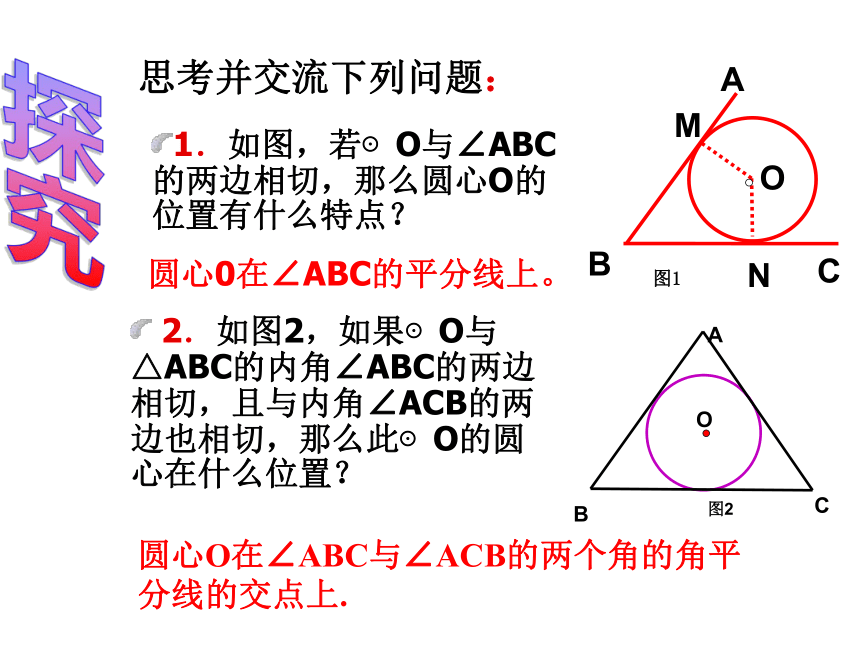
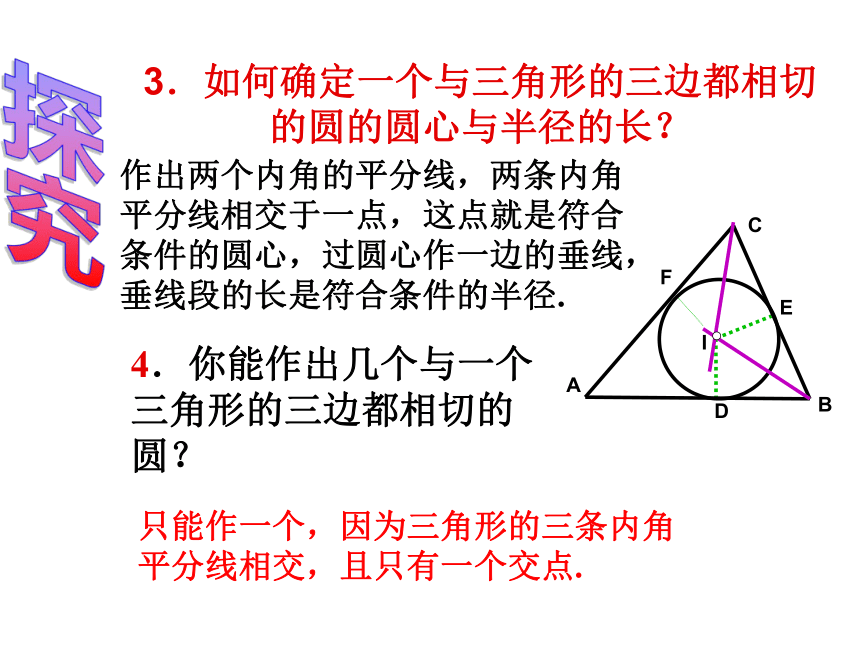
判定:到这个角的两边距离相等的点在这个角的平分线上。知识回顾2)不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:要在三角形木料上裁下一块圆形用料,且使圆的面积最大,他就找我这个数学老师帮忙,同学们,你能帮他确定一下吗?设疑激思思考并交流下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心O在∠ABC与∠ACB的两个角的角平分线的交点上. OMABCN图1探究3.如何确定一个与三角形的三边都相切的圆的圆心与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆? 作出两个内角的平分线,两条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径. 只能作一个,因为三角形的三条内角
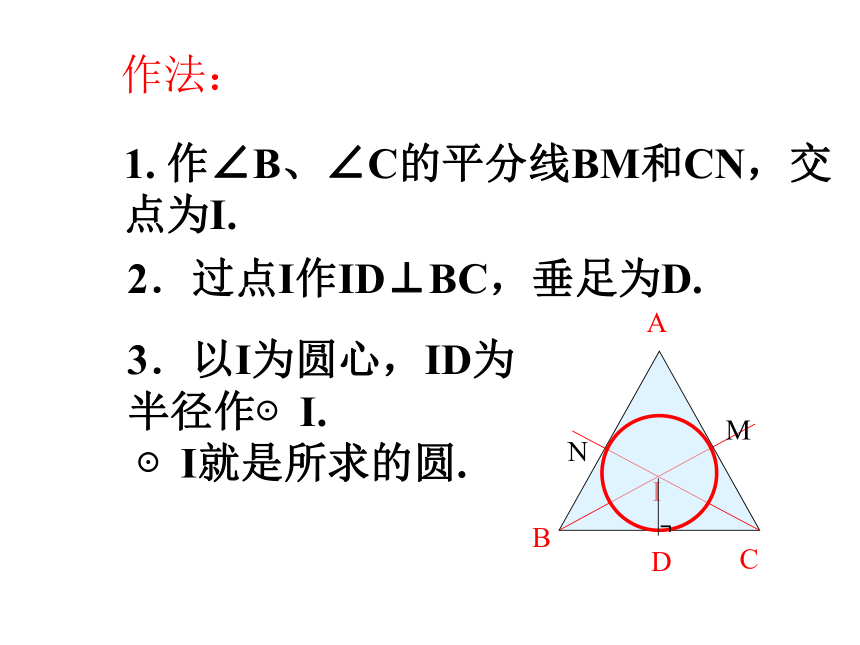
平分线相交,且只有一个交点. IFCABED探究作法: ABC1. 作∠B、∠C的平分线BM和CN,交点为I. I2.过点I作ID⊥BC,垂足为D. 3.以I为圆心,ID为
半径作⊙I.
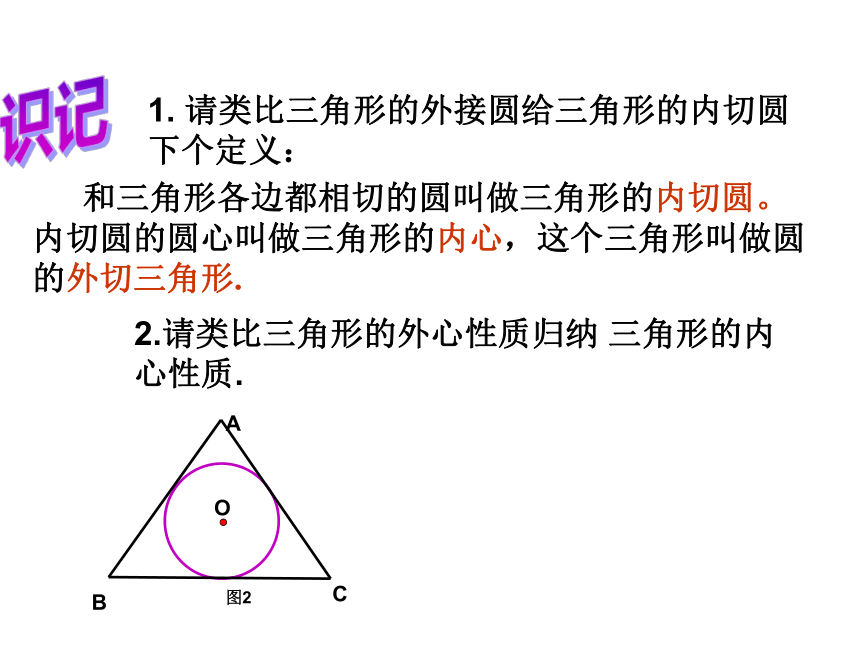
⊙I就是所求的圆. MN?1. 请类比三角形的外接圆给三角形的内切圆下个定义:识记2.请类比三角形的外心性质归纳 三角形的内心性质. 和三角形各边都相切的圆叫做三角形的内切圆。 内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.1. 三角形的内心到三角形各边的距离相等( )
2. 三角形的外心到三角形各顶点的距离相等 ( )
3. 三角形的内心不一定在三角形的内部 ( )
4. 一个三角形只有一个内切圆;一个圆也只有一个外切三角形( )
× × 判断对错:√√例1:如图,在△ABC中,∠BAC=500 , 点I
是内心,求∠BIC的度数。 分析: ∠BI C= ? ∠1 + ∠3= ? I为△ABC的内心 BI是∠ABC的角平分线 CI是∠ACB的角平分线 ABCI2143ABCI2143变式2:在△ABC中,点I是内心,
∠BIC=120°,求∠BAC的度数。变式3:在△ABC中,点I是内心,
∠BAC=α,求∠BIC的度数。变式1:如图,在△ABC中,∠BAC=500 ,
点I是外心,求∠BIC的度数。 例2、如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E.
求证:BE=IE提示:欲证BE=IE
需证∠ BIE= ∠ IBE
把∠ BIE转化为两圆周角之和5课堂小结: 1.谈谈本节课你学到了什么?
认识了三角形的内切圆,内心,圆的外切三角形;
掌握了作一个三角形的内切圆的方法;
理解并掌握了内心的性质
类比思想,整体思想,从特殊到一般的思想
2.本节课运用了什么数学思想?作业:
1.P42练习1、2、3题 2.课外拓展:求等边三角形的内切圆半
径r与外接圆半径R的比。r思考题:如图:已知直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:F谢谢各位领导和同行的指导!
判定:到这个角的两边距离相等的点在这个角的平分线上。知识回顾2)不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:要在三角形木料上裁下一块圆形用料,且使圆的面积最大,他就找我这个数学老师帮忙,同学们,你能帮他确定一下吗?设疑激思思考并交流下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心O在∠ABC与∠ACB的两个角的角平分线的交点上. OMABCN图1探究3.如何确定一个与三角形的三边都相切的圆的圆心与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆? 作出两个内角的平分线,两条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径. 只能作一个,因为三角形的三条内角
平分线相交,且只有一个交点. IFCABED探究作法: ABC1. 作∠B、∠C的平分线BM和CN,交点为I. I2.过点I作ID⊥BC,垂足为D. 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆. MN?1. 请类比三角形的外接圆给三角形的内切圆下个定义:识记2.请类比三角形的外心性质归纳 三角形的内心性质. 和三角形各边都相切的圆叫做三角形的内切圆。 内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.1. 三角形的内心到三角形各边的距离相等( )
2. 三角形的外心到三角形各顶点的距离相等 ( )
3. 三角形的内心不一定在三角形的内部 ( )
4. 一个三角形只有一个内切圆;一个圆也只有一个外切三角形( )
× × 判断对错:√√例1:如图,在△ABC中,∠BAC=500 , 点I
是内心,求∠BIC的度数。 分析: ∠BI C= ? ∠1 + ∠3= ? I为△ABC的内心 BI是∠ABC的角平分线 CI是∠ACB的角平分线 ABCI2143ABCI2143变式2:在△ABC中,点I是内心,
∠BIC=120°,求∠BAC的度数。变式3:在△ABC中,点I是内心,
∠BAC=α,求∠BIC的度数。变式1:如图,在△ABC中,∠BAC=500 ,
点I是外心,求∠BIC的度数。 例2、如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E.
求证:BE=IE提示:欲证BE=IE
需证∠ BIE= ∠ IBE
把∠ BIE转化为两圆周角之和5课堂小结: 1.谈谈本节课你学到了什么?
认识了三角形的内切圆,内心,圆的外切三角形;
掌握了作一个三角形的内切圆的方法;
理解并掌握了内心的性质
类比思想,整体思想,从特殊到一般的思想
2.本节课运用了什么数学思想?作业:
1.P42练习1、2、3题 2.课外拓展:求等边三角形的内切圆半
径r与外接圆半径R的比。r思考题:如图:已知直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:F谢谢各位领导和同行的指导!
