北师八上2.6实数

(共26张PPT)
第二章 实数
2.6实数
北师大版 数学 八年级 上册
学习目标
1、了解在有理数范围内的运算及运算法则、运算性质等在实数内仍然成立。
2、能熟练地进行实数运算。
3、在实数运算时，根据问题的要求取其近似值，转化有理数计算。
情景导入
（1）什么是有理数？有理数怎样分类？
（2）什么是无理数？带根号的数都是无理数吗？
（1）整数和分数统称为有理数；有理数可以分为整数和分数；也可以分为正有理数、0和负有理数.
（2）无限不循环小数是无理数，带根号的数不一定是无理数.
情景导入
１．圆周率π及一些含有π的数（如2π-1）
2．开不尽方的数
3．有一定的规律，但不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
探索新知
实数的概念及分类
一
（1）请把下列有理数写成小数的形式，你有什么发现？任何有理数都能写成有限小数和无限循环小数吗？
（2）请用计算器把 和 写成小数的形式，你有什么发现？像这样的数我们把它叫什么数？你还能说出一些这样的数吗？
探索新知
事实上，任何一个有理数都可以写成有限小数或无限循环小数.
反过来，任何有限小数或无限循环小数也都是有理数.
探索新知
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗？
0.1010010001…〔两个1之间依次多1个0〕
－168.3232232223…〔两个3之间依次多1个2〕
=1.41421356237309504880168…
=1.70997594667669698935310…
探索新知
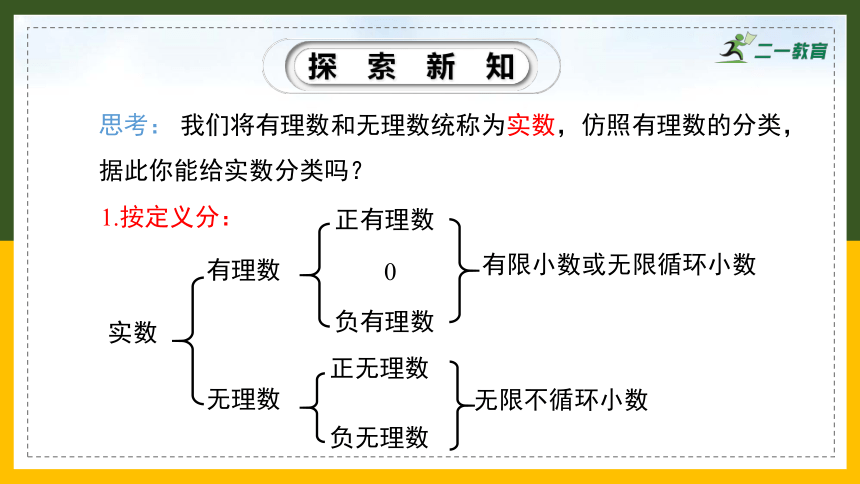
思考： 我们将有理数和无理数统称为实数，仿照有理数的分类，据此你能给实数分类吗？
1.按定义分：
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
探索新知
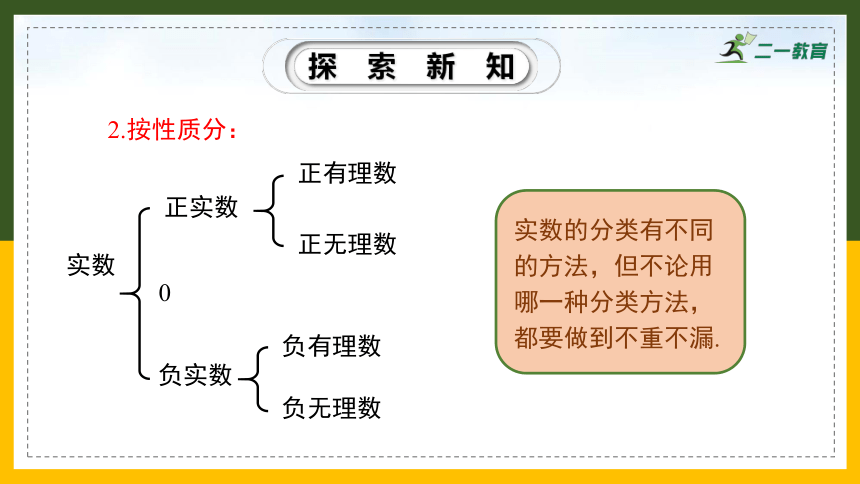
2.按性质分：
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
实数的分类有不同的方法，但不论用哪一种分类方法，都要做到不重不漏.
探索新知
实数范围内的相关概念
二
1．3-π的绝对值是 ．
2．想一想：a是一个实数，它的相反数是 ，它的绝对值是 ，当a≠0时，它的倒数是 ．
探索新知
在实数范围内 ，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样．
与 互为相反数
与 互为倒数
例如：
总结归纳
探索新知
1.相反数：a与－a互为相反数；0的相反数仍是0；
2.倒数：当a≠0时，a与 互为倒数（0没有倒数）；
3.绝对值：正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0；
即：
探索新知
例1.求下列各数的相反数、倒数和绝对值：
探索新知
实数和有理数一样，可以进行加、减、乘、除、乘方运算，而且有理数的运算法则与运算律对实数仍然使用.
例如：
探索新知
实数与数轴上点的对应关系
三
如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点从原点到达A点，则点A的坐标为多少？
-4
-2
0
1
2
3
4
-1
-3
无理数π可以用数轴上的点来表示.
A
问题1： 无理数能在数轴上表示出来吗？
探索新知
－2
－1
0
1
2
问题2：你能在数轴上表示出吗？呢？
0
1
2
3
-1
1
2
探索新知
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。
即实数和数轴上的点是一一对应的。
在数轴上的两个点，右边的点表示的实数总比左边的点表示的实数大。
总结归纳
当堂检测
1.下列说法：
①无限小数是无理数；②3.14是无理数；
③ 是有理数；④无理数都可以用数轴上的点表示；
⑤实数都是无理数；⑥无理数是开方开不尽的数；
⑦无理数是无限不循环小数；⑧实数包括有理数.其中
正确的说法有（　C　）
A. 1个 B. 2个 C. 3个 D. 4个
C
当堂检测
2. 在实数 ， ， ， 中，有理数是（　C　）
A. B. C. D.
C
3. 下列各组数中互为相反数的一组是（　C　）
A. 2与 B. 与
C. －2与 D. 2与
C
当堂检测
4. 实数 a ， b 在数轴上的对应点的位置如图所示，下列
式子成立的是（　D　）
A. a ＞ b B. ＜
C. a ＋ b ＞0 D. ＜0
D
当堂检测
5. （1） 的倒数是 　 　；
（2）计算： ＋（－1）3－ － ＝ ；
（3）化简： ＋ ＋ ＝ .
　
0　
4－
　
（4）的相反数是 　，绝对值是 　;
没有倒数的实数是　 　.
　 0　


当堂检测
6. 把无理数 ， ， ， 表示在数轴上，其中，在 与 之间的是______.
7. 的相反数为_________.
8. 如图，数轴上点 所表示的数为_________.
当堂检测
9.把下列各数填在相应的集合内：
， ， ， ， ， ， ， ， ， …(相邻两个 之间 的个数逐次加 ， ， .
整数集合 ____________________… ；
负分数集合 ________________________________… ；
无理数集合 _____________________________
_____________ ______________… .
， ，
， ， ，
， ，
（相邻两个 之间 的个数逐次加 ）
当堂检测
10. 如图，一只蚂蚁从点 沿数轴向右爬 个单位长度到达点 ，点 表示 ，设点 所表示的数为 .
（1） 求 的值；
解： .
（2） 求 的值.
解：
.
实
数
有理数和无理数统称实数
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
实数与数轴上的点一一对应
感谢收看