青岛版数学八年级上册 2.2 轴对称的基本性质(1)课件(共15张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.2 轴对称的基本性质(1)课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 104.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 08:27:49 | ||
图片预览





文档简介
(共15张PPT)
第2章 圆形的轴对称
2.2 轴对称的基本性质(1)
情景导航
1.下面图形是轴对称图形吗?如果是,请画出对称轴。
2.什么叫做轴对称、什么叫做对称轴、什么叫做对称点?
A
A′
O
如图:把一张纸对折后扎一个孔,
然后展开铺平。
连接得到的两个小孔A和A′,
线段AA′与折痕MN交点为O,
1.线段AA′与直线MN的位置关系?
2.你还发现了哪些等量关系?
M
N
垂直,即AA′⊥MN
平分,即AO=A′O
实验与探究
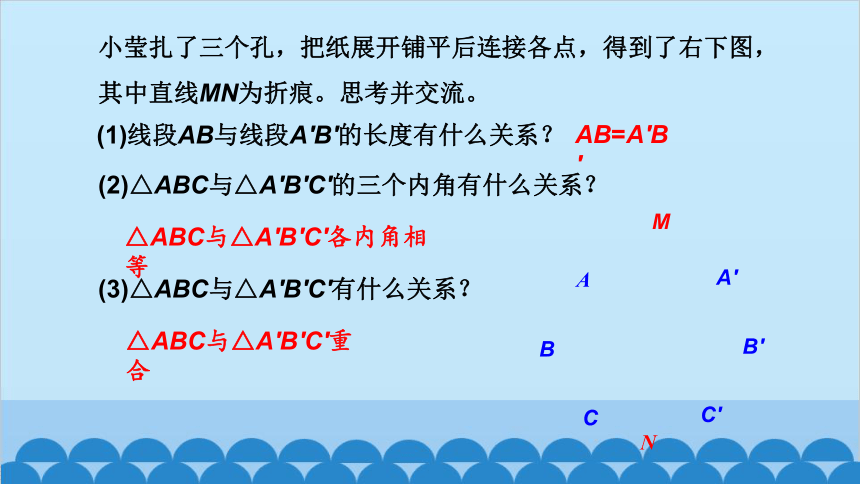
小莹扎了三个孔,把纸展开铺平后连接各点,得到了右下图,其中直线MN为折痕。思考并交流。
A
A′
B
B′
C
C′
M
N
(1)线段AB与线段A′B′的长度有什么关系?
(2)△ABC与△A′B′C′的三个内角有什么关系?
(3)△ABC与△A′B′C′有什么关系?
AB=A′B′
△ABC与△A′B′C′各内角相等
△ABC与△A′B′C′重合
轴对称的基本性质:
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
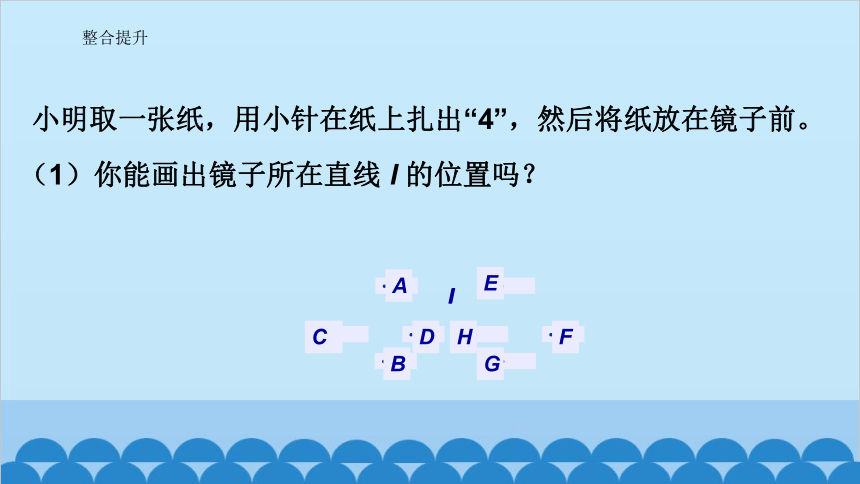
小明取一张纸,用小针在纸上扎出“4”,然后将纸放在镜子前。
(1)你能画出镜子所在直线 l 的位置吗?
l
整合提升
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(2)图中点A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CAB= ,∠ACD= .
E、G、F、H
EF、EG
FH
∠FEG
∠EFH
(3)连接AE、BG, AE与BG平行吗?为什么?
因为 A和E,B和G是关于直线 l 的对称点,
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
所以 l⊥AE ,l⊥BG.
所以 AE ∥BG.
解:平行。
(4)AE与BG平行,能说明轴对称图形对称点的连线一定互相平行吗?
解:不一定。
如图,对称点的连线DH、CF就不互相平行,而是在同一条直线上,从而说明轴对称图形对称点的连线互相平行或在同一条直线上。
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(5)延长线段CA、FE,连接CB、FG并延长,作直线AB、EG,
你有什么发现吗?
解:轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行。
例1
如图,做出△BCD关于直线 l 的对称图形。
B′
C
C′
B
D
l
解: 如图,分别作出点B、C、D三点关于直线l的对称点B′, C′ ,D三点,
△ B′C′ D就是求作的图形。
分别连接B′C′,C′D,DB′
例2
l
75°
γ
a
b
δ
2.29
3.20
3.44
c
β
43°
α
右图中两个三角形关于直线l成轴对称。如果三角形的部分边长(单位:厘米)和角的度数如图所示,求未知的边长和角的度数。
解:因为这两个三角形关于直线 l 成轴对称,它们的对应角相等,对应线段相等,所以
a=3.20厘米,b=3.44厘米,c=2.29厘米;
∠α=75°,∠γ=43°。
又因为三角形的内角和为180°, 所以
∠δ=∠β=180°-75°-43°=62°
练习:将正方形纸片两次对折,并剪出一个菱形小洞后铺平,
得到的图形是( ).
C
课后作业
完成练习T1、2
谢谢观看
谢谢观看
第2章 圆形的轴对称
2.2 轴对称的基本性质(1)
情景导航
1.下面图形是轴对称图形吗?如果是,请画出对称轴。
2.什么叫做轴对称、什么叫做对称轴、什么叫做对称点?
A
A′
O
如图:把一张纸对折后扎一个孔,
然后展开铺平。
连接得到的两个小孔A和A′,
线段AA′与折痕MN交点为O,
1.线段AA′与直线MN的位置关系?
2.你还发现了哪些等量关系?
M
N
垂直,即AA′⊥MN
平分,即AO=A′O
实验与探究
小莹扎了三个孔,把纸展开铺平后连接各点,得到了右下图,其中直线MN为折痕。思考并交流。
A
A′
B
B′
C
C′
M
N
(1)线段AB与线段A′B′的长度有什么关系?
(2)△ABC与△A′B′C′的三个内角有什么关系?
(3)△ABC与△A′B′C′有什么关系?
AB=A′B′
△ABC与△A′B′C′各内角相等
△ABC与△A′B′C′重合
轴对称的基本性质:
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
小明取一张纸,用小针在纸上扎出“4”,然后将纸放在镜子前。
(1)你能画出镜子所在直线 l 的位置吗?
l
整合提升
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(2)图中点A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CAB= ,∠ACD= .
E、G、F、H
EF、EG
FH
∠FEG
∠EFH
(3)连接AE、BG, AE与BG平行吗?为什么?
因为 A和E,B和G是关于直线 l 的对称点,
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
所以 l⊥AE ,l⊥BG.
所以 AE ∥BG.
解:平行。
(4)AE与BG平行,能说明轴对称图形对称点的连线一定互相平行吗?
解:不一定。
如图,对称点的连线DH、CF就不互相平行,而是在同一条直线上,从而说明轴对称图形对称点的连线互相平行或在同一条直线上。
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(5)延长线段CA、FE,连接CB、FG并延长,作直线AB、EG,
你有什么发现吗?
解:轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行。
例1
如图,做出△BCD关于直线 l 的对称图形。
B′
C
C′
B
D
l
解: 如图,分别作出点B、C、D三点关于直线l的对称点B′, C′ ,D三点,
△ B′C′ D就是求作的图形。
分别连接B′C′,C′D,DB′
例2
l
75°
γ
a
b
δ
2.29
3.20
3.44
c
β
43°
α
右图中两个三角形关于直线l成轴对称。如果三角形的部分边长(单位:厘米)和角的度数如图所示,求未知的边长和角的度数。
解:因为这两个三角形关于直线 l 成轴对称,它们的对应角相等,对应线段相等,所以
a=3.20厘米,b=3.44厘米,c=2.29厘米;
∠α=75°,∠γ=43°。
又因为三角形的内角和为180°, 所以
∠δ=∠β=180°-75°-43°=62°
练习:将正方形纸片两次对折,并剪出一个菱形小洞后铺平,
得到的图形是( ).
C
课后作业
完成练习T1、2
谢谢观看
谢谢观看
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
