九下圆周角和圆心角的关系第一课时课件
图片预览


文档简介
课件27张PPT。3.4 圆周角和圆心角的关系
第一课时九年级数学(下)第三章 圆1.圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.2.圆也是中心对称图形.它的对称中心就是圆心.知识回顾4.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。 5.定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
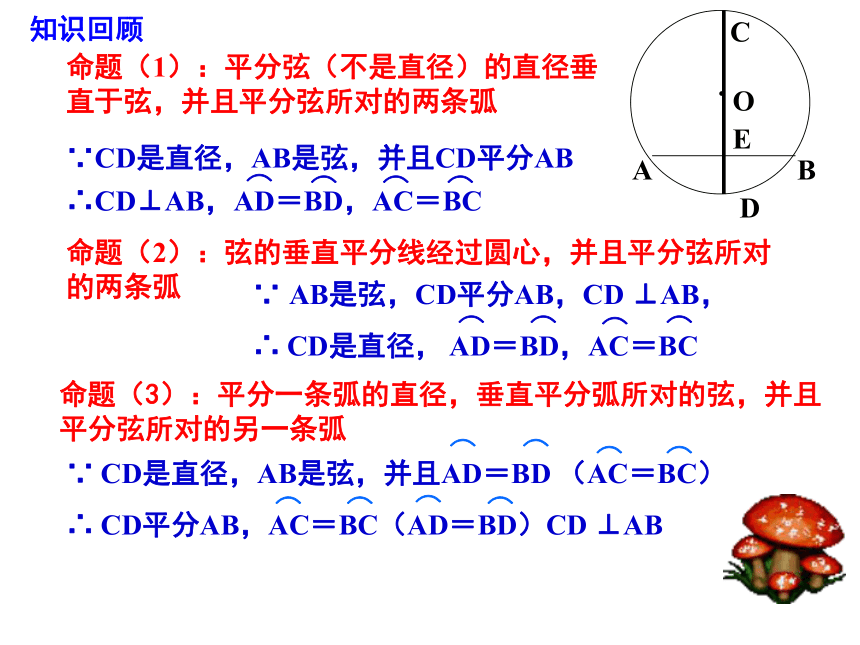
3.顶点在圆心的角叫做圆心角.垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对 的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧垂径定理知识回顾命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧∵ AB是弦,CD平分AB,CD ⊥AB,
∴ CD是直径, AD=BD,AC=BC命题(3):平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧∵ CD是直径,AB是弦,并且AD=BD (AC=BC)
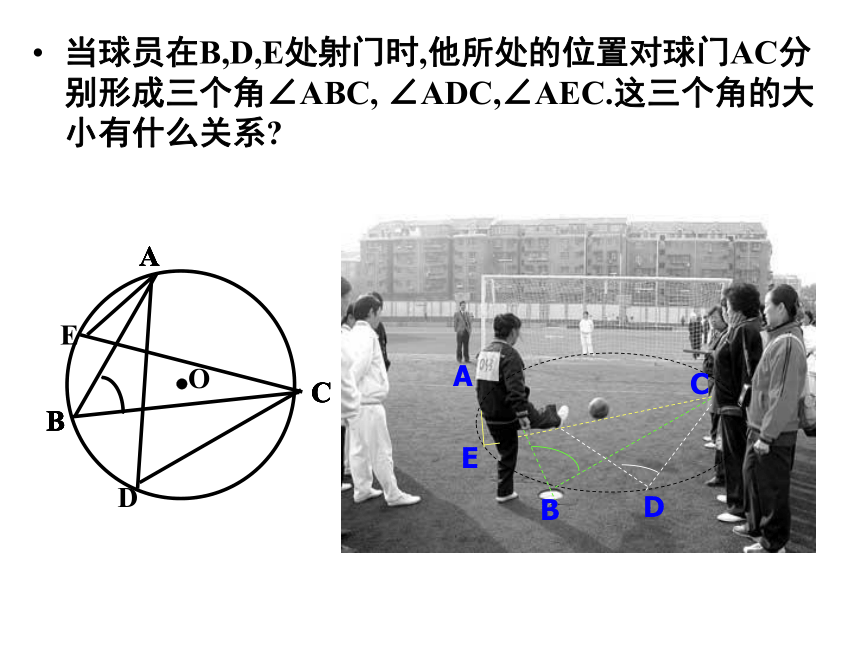
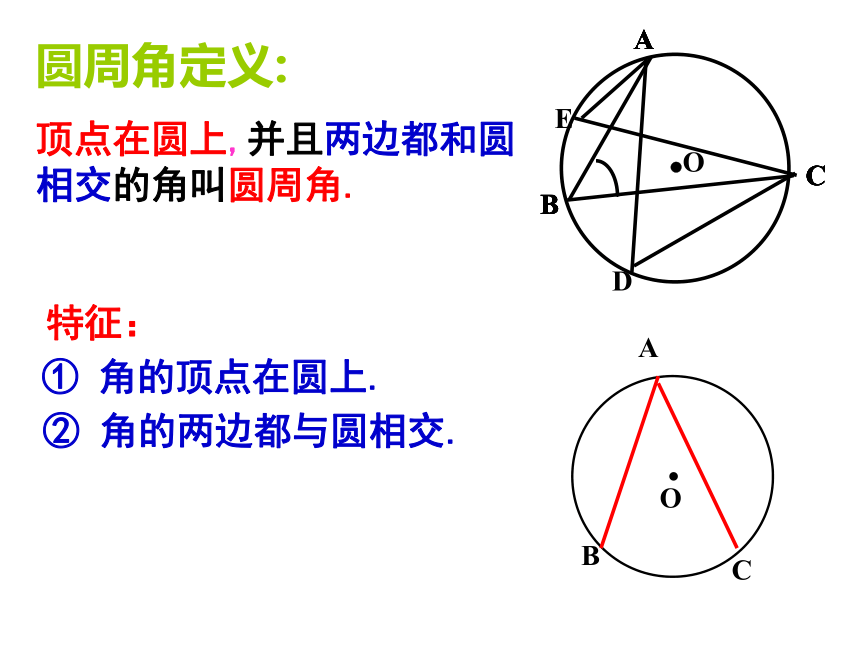
∴ CD平分AB,AC=BC(AD=BD)CD ⊥AB 知识回顾当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义:
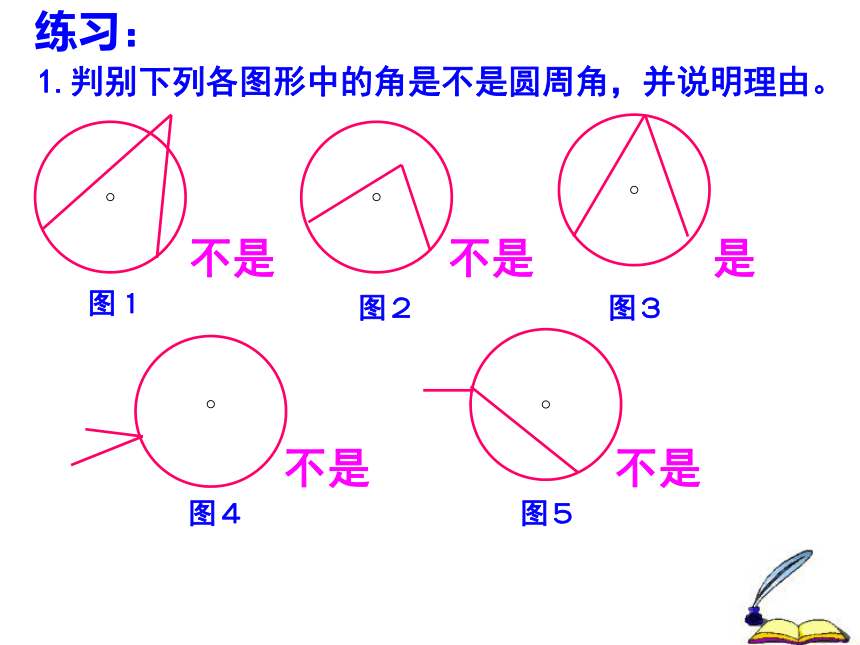
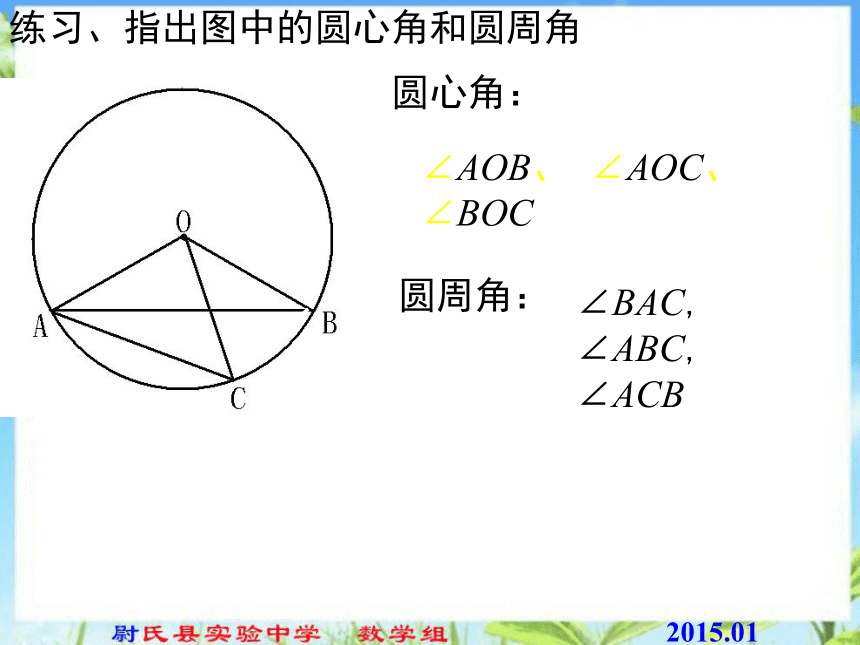
顶点在圆上,并且两边都和圆相交的角叫圆周角.练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5练习、指出图中的圆心角和圆周角圆心角:
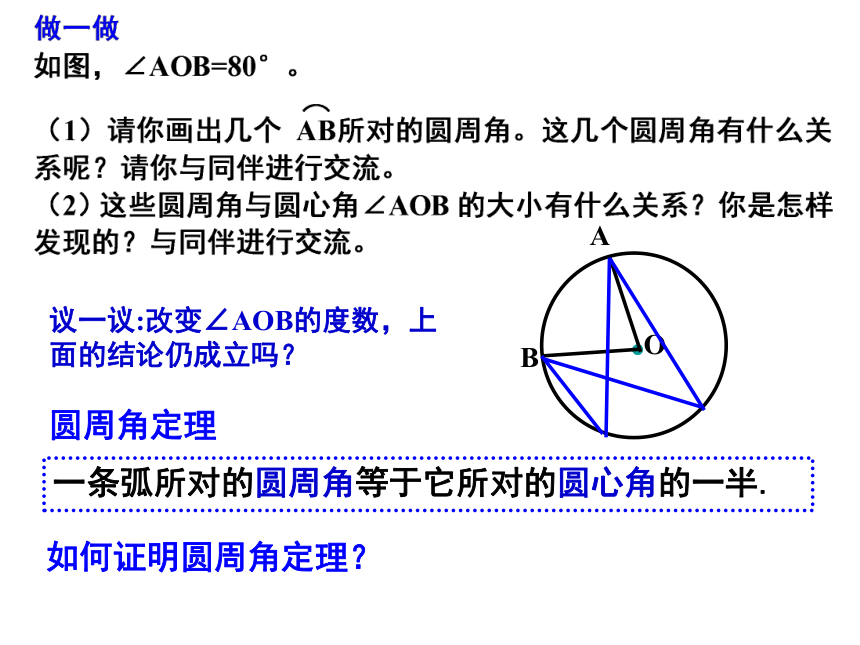
圆周角:∠AOB、 ∠AOC、 ∠BOC∠BAC, ∠ABC, ∠ACB议一议:改变∠AOB的度数,上面的结论仍成立吗?一条弧所对的圆周角等于它所对的圆心角的一半.如何证明圆周角定理?圆周角定理类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系? 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.如图,观察弧AB所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?说说你的想法,并与同伴交流.证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ACB)的一边(BC)上时,圆周角∠ACB与圆心角∠AOB的大小关系∵∠AOB是△ACO的外角,∴∠AOB=∠C+∠A.∵OA=OC,∴∠A=∠C.∴∠AOB=2∠C.证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?过点C作直径CD.由1可得:∠ACD+∠BCD= (∠AOD+∠BOD)证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.过点C作直径CD.由1可得:3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.分类讨论、转化如图所示,∠ADB、∠ACB、∠AOB分别是什么角?它们有何共同点? ∠ADB与∠ACB有什么关系? 同弧 所对的圆周角相等.(等弧)都等于这条弧所对的圆心角的一半.圆周角定理推论:相等的圆周角所对的弧相等.在同圆或等圆中,在射门游戏中,当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?你能用圆周角定理去解决问题。想一想:
同弧或等弧所对的圆周角相等。⑴“同弧或等弧”能否改为“同弦或等弦”?⑵ “同圆或等圆”这一条件能否省去?不能不能同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?解:在⊙O中,∠BOC=50°图中有几对相似三角形?又∵∠AOB=2 ∠BOC解:∠ACB= 2 ∠BAC,理由:即∠ACB= 2 ∠BAC解:∵∠BCD=100°
∴优弧所对的圆心角∠BOD=2∠BCD=200°
∴劣弧所对的圆心角
∠BOD=360°-200°=160°3.为什么电影院的座位排列呈弧形,说一说这设计的合理性。 答:有些电影院的座位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等。数学理解4.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角” 。数学理解这节课有何收获?!你美丽的圆1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.2.圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.同弧 所对的圆周角相等.(等弧)3.圆周角定理推论:相等的圆周角所对的弧相等.4.在同圆或等圆中,相等的弦所对的弧不一定相等.5.在同圆或等圆中,再见
第一课时九年级数学(下)第三章 圆1.圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.2.圆也是中心对称图形.它的对称中心就是圆心.知识回顾4.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。 5.定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
3.顶点在圆心的角叫做圆心角.垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对 的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧垂径定理知识回顾命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧∵ AB是弦,CD平分AB,CD ⊥AB,
∴ CD是直径, AD=BD,AC=BC命题(3):平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧∵ CD是直径,AB是弦,并且AD=BD (AC=BC)
∴ CD平分AB,AC=BC(AD=BD)CD ⊥AB 知识回顾当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5练习、指出图中的圆心角和圆周角圆心角:
圆周角:∠AOB、 ∠AOC、 ∠BOC∠BAC, ∠ABC, ∠ACB议一议:改变∠AOB的度数,上面的结论仍成立吗?一条弧所对的圆周角等于它所对的圆心角的一半.如何证明圆周角定理?圆周角定理类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系? 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.如图,观察弧AB所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?说说你的想法,并与同伴交流.证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ACB)的一边(BC)上时,圆周角∠ACB与圆心角∠AOB的大小关系∵∠AOB是△ACO的外角,∴∠AOB=∠C+∠A.∵OA=OC,∴∠A=∠C.∴∠AOB=2∠C.证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?过点C作直径CD.由1可得:∠ACD+∠BCD= (∠AOD+∠BOD)证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.过点C作直径CD.由1可得:3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.分类讨论、转化如图所示,∠ADB、∠ACB、∠AOB分别是什么角?它们有何共同点? ∠ADB与∠ACB有什么关系? 同弧 所对的圆周角相等.(等弧)都等于这条弧所对的圆心角的一半.圆周角定理推论:相等的圆周角所对的弧相等.在同圆或等圆中,在射门游戏中,当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?你能用圆周角定理去解决问题。想一想:
同弧或等弧所对的圆周角相等。⑴“同弧或等弧”能否改为“同弦或等弦”?⑵ “同圆或等圆”这一条件能否省去?不能不能同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?解:在⊙O中,∠BOC=50°图中有几对相似三角形?又∵∠AOB=2 ∠BOC解:∠ACB= 2 ∠BAC,理由:即∠ACB= 2 ∠BAC解:∵∠BCD=100°
∴优弧所对的圆心角∠BOD=2∠BCD=200°
∴劣弧所对的圆心角
∠BOD=360°-200°=160°3.为什么电影院的座位排列呈弧形,说一说这设计的合理性。 答:有些电影院的座位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等。数学理解4.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角” 。数学理解这节课有何收获?!你美丽的圆1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.2.圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.同弧 所对的圆周角相等.(等弧)3.圆周角定理推论:相等的圆周角所对的弧相等.4.在同圆或等圆中,相等的弦所对的弧不一定相等.5.在同圆或等圆中,再见
