23.3.3相似三角形的性质 同步练习(含答案)华师大版数学九年级上册
文档属性
| 名称 | 23.3.3相似三角形的性质 同步练习(含答案)华师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 421.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-27 19:25:53 | ||
图片预览



文档简介
23.3.3相似三角形的性质 同步练习
一、单选题
1.D、E是△ABC的边AB、AC的中点,△ABC、△ADE的面积分别为S、S1,则下列结论中,错误的是( )
A.DE∥BC B.DE=BC C.S1=S D.S1=S
2.如图,图1是可折叠的熨衣架的实物图,图2是它的侧面示意图,与相交于点O,,根据图2中的数据可得x的值为( )
A.0.4 B.0.8 C.1 D.1.6
3.如图,在中,与相交于点,为的中点,连接并延长交于点,则:( )
A.: B.: C.: D.:
4.如图,中,,垂足为D,,垂足为E,与相交于点F.连接.给出以下四个结论:①;②;③;④.其中一定正确的是( )
A.①②③ B.①②④ C.②③ D.①②③④
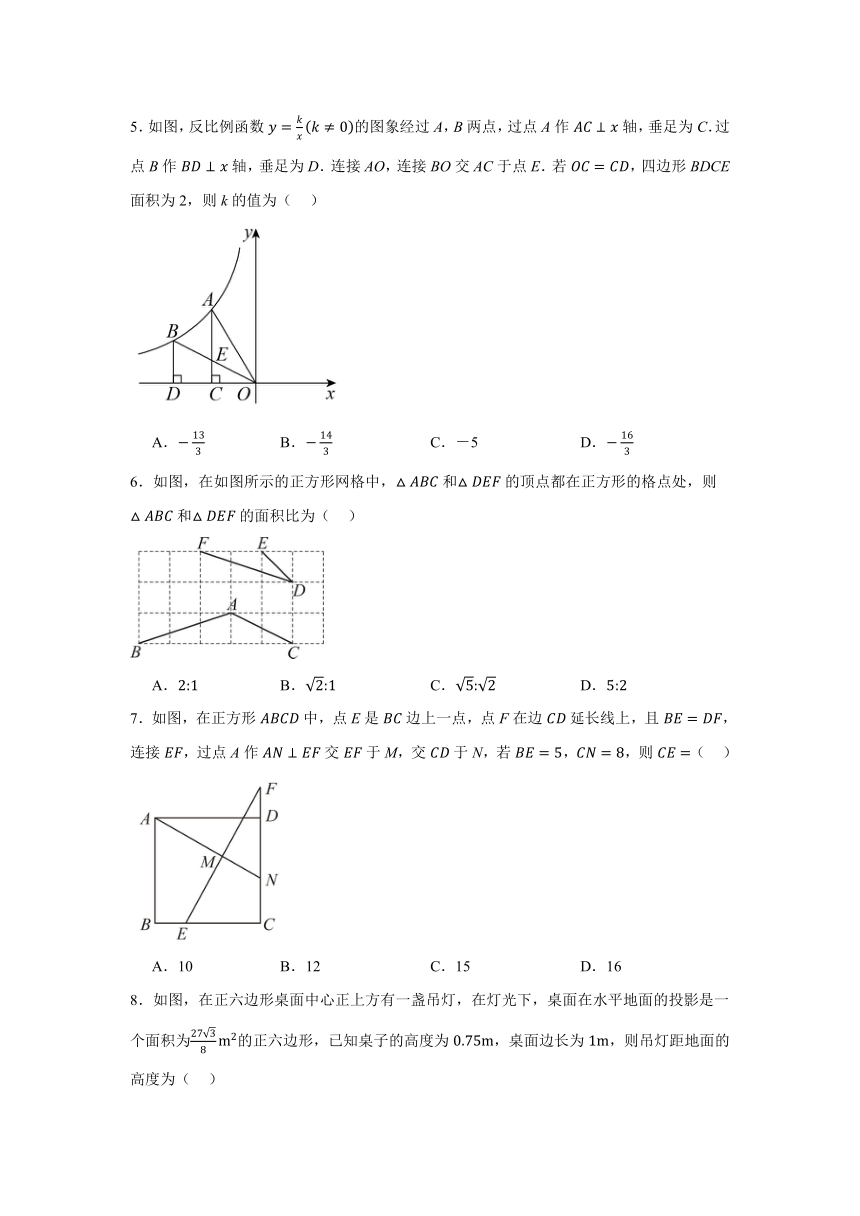
5.如图,反比例函数的图象经过A,B两点,过点A作轴,垂足为C.过点B作轴,垂足为D.连接AO,连接BO交AC于点E.若,四边形BDCE面积为2,则k的值为( )
A. B. C.-5 D.
6.如图,在如图所示的正方形网格中,和的顶点都在正方形的格点处,则和的面积比为( )
A. B. C. D.
7.如图,在正方形中,点E是边上一点,点F在边延长线上,且,连接,过点A作交于M,交于N,若,,则( )
A.10 B.12 C.15 D.16
8.如图,在正六边形桌面中心正上方有一盏吊灯,在灯光下,桌面在水平地面的投影是一个面积为的正六边形,已知桌子的高度为,桌面边长为,则吊灯距地面的高度为( )
A. B. C. D.
二、填空题
9.如图,在中,点、分别在边,上,,,,则的长为 .
10.如图,在和中,,,则的度数为 .
11.在直角梯形中,,,,,,点P是边上一动点,若与相似,则的长度是 .
12.如图,在中,,,为边上的一点,且.若的面积为1,则的面积为 .
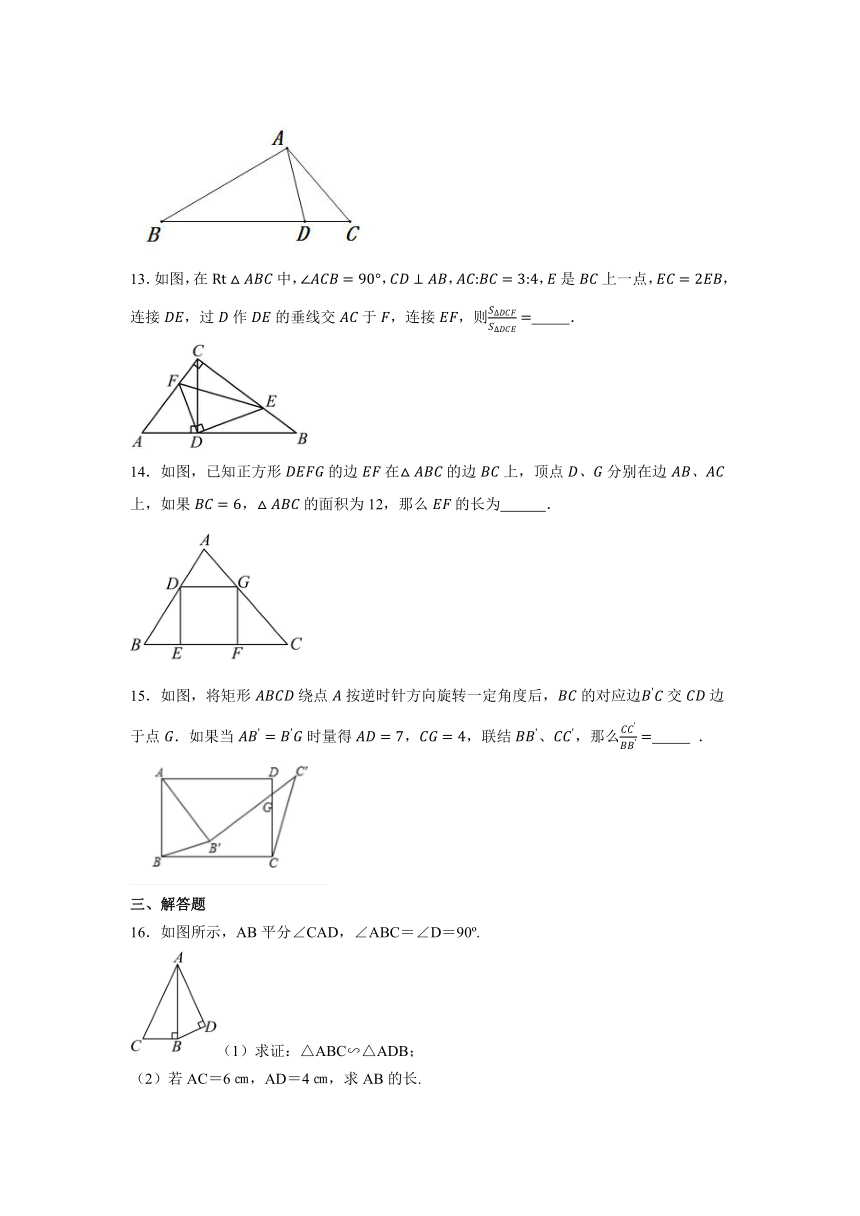
13.如图,在中,,,,是上一点,,连接,过作的垂线交于,连接,则 .
14.如图,已知正方形的边在的边上,顶点分别在边上,如果,的面积为12,那么的长为 .
15.如图,将矩形绕点按逆时针方向旋转一定角度后,的对应边交边于点.如果当时量得,,联结、,那么 .
三、解答题
16.如图所示,AB平分∠CAD,∠ABC=∠D=90 .
(1)求证:△ABC∽△ADB;
(2)若AC=6㎝,AD=4㎝,求AB的长.
17.已知:如图,△ABC中,点D、E、F分别在边AB、BC、AC上,且DE∥AC,=.
(1)求证:DF∥BC;
(2)如果DF=2,BE=4,求的值.
18.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
19.如图,矩形ABCD中,AB=4,BC=6,E为线段AD上一动点,连接CE,过点B作BF⊥CE,交射线CD于点F,垂足为P.
(1)求证:CED∽BCF;
(2)当F为CD的中点时,求tan∠BAP的值;
(3)若ABP为等腰三角形时,直接写出DE的长.
20.在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为 ;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是 .(直接给出结论无须证明)
参考答案:
1.D
2.A
3.D
4.B
5.D
6.D
7.C
8.A
9.10
10.40°
11.1或2.8或6
12.3
13.
14.
15.
16.(1)证明:∵AB平分∠CAD ∴∠CAB=∠BAD
∵∠ABC=∠D=90 ∴△ABC∽△ADB
(2)由(1)得△ABC∽△ADB
∴ ,即AB2=AC AD
∴
17.(1)证明:∵DE∥AC,
∴=,
又∵=.
∴=,
∴DF∥BC;
(2)∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,
∴CE=DF=2,
∵BE=4,
∴BC=4+2=6,
∵DF∥BC,
∴,
∴=.
18.解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB10cm;
分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t;
∴t=1或时,△BPQ∽△BCA;
(2)分三种情况:
①当PB=PQ时,如图,过P作PH⊥BQ,
则BHBQ=4﹣2t,PB=5t,
∴PH∥AC,
∴,即解得:t;
②当PB=BQ时,即5t=8﹣4t,
解得:t;
③当BQ=PQ时,如图,过Q作QG⊥AB于G,
则BGPBt,BQ=8﹣4t,
∵,,
∴,
∴即,
解得:t;
综上所述:△BPQ是等腰三角形时t的值为:或或;
(3)如图,过P作PM⊥BC于点M,则PB=5t,
∵AC⊥BC,,
∴,
∴△PMB∽△ACB,
∴,
∴PM=3t,MC=8﹣4t,CQ=4t,
根据勾股定理得,CP2=PM2+MC2=25t2﹣64t+64,
∵CP=CQ,
∴25t2﹣64t+64=16t2,
∴t(不符题意,舍去)或t,
∴CP=CQ时,t;
(4)如图,过P作PM⊥BC于点M,AQ,CP交于点N,
由(3)可知,PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t.
19.(1)∵四边形是矩形,
,
,
,
,
.
(2)如图1,
过点作于点,交于点,
,
,
,
,
;
,
,
,
解得,
,
∴四边形是矩形,
,
,
,
,
,
解得,
,
,
,
解得,
,
(3)当时,如图2,
作于点H,则AH=BH,
,
,
,
,
,
,
∴AE,
∴DE=;
当PA=AB时,如图3,
作AM⊥BP于点M,则,
,
,
,
,
,
,
∴整理得CF,
,
,
;
当BP=AB=4时,如图4,
则,
,
,
.
综上所述,DE的长为或3或.
20.(1)解:∵ΔABC是等边三角形,D是BC边的中点,
∴∠BAD=30°,
∵线段AD和AE关于直线AB对称,
∴DE⊥AB,
∴∠ADE+∠BAD=90°,
∴∠ADE=60°,
∴∠BDE=90°-60°=30°;
故答案为:30°
(2)解:解:①作图如下:
②如图,连接AE.
为等边三角形,
∴∠DAE=60°,AD=AE,
为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,
∴∠BAE=∠CAD,
,
;
(3)解: 如图,连接AE,
∵AC=kBC,AD=kDE,
∴,即,
∵∠ADE=∠C,
∴△ADE∽△ACB,
∴∠AED=∠ABC,∠EAD=∠BAC,
∴∠EAB=∠DAC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AED=∠ADE,
∴AE=AD,
∴△AEB≌△ADC,
∴CD=BE;
∵BC=BD+CD,
∴BC=BD+BE,
∵AC=kBC,
∴k(BE+BD)=AC.
一、单选题
1.D、E是△ABC的边AB、AC的中点,△ABC、△ADE的面积分别为S、S1,则下列结论中,错误的是( )
A.DE∥BC B.DE=BC C.S1=S D.S1=S
2.如图,图1是可折叠的熨衣架的实物图,图2是它的侧面示意图,与相交于点O,,根据图2中的数据可得x的值为( )
A.0.4 B.0.8 C.1 D.1.6
3.如图,在中,与相交于点,为的中点,连接并延长交于点,则:( )
A.: B.: C.: D.:
4.如图,中,,垂足为D,,垂足为E,与相交于点F.连接.给出以下四个结论:①;②;③;④.其中一定正确的是( )
A.①②③ B.①②④ C.②③ D.①②③④
5.如图,反比例函数的图象经过A,B两点,过点A作轴,垂足为C.过点B作轴,垂足为D.连接AO,连接BO交AC于点E.若,四边形BDCE面积为2,则k的值为( )
A. B. C.-5 D.
6.如图,在如图所示的正方形网格中,和的顶点都在正方形的格点处,则和的面积比为( )
A. B. C. D.
7.如图,在正方形中,点E是边上一点,点F在边延长线上,且,连接,过点A作交于M,交于N,若,,则( )
A.10 B.12 C.15 D.16
8.如图,在正六边形桌面中心正上方有一盏吊灯,在灯光下,桌面在水平地面的投影是一个面积为的正六边形,已知桌子的高度为,桌面边长为,则吊灯距地面的高度为( )
A. B. C. D.
二、填空题
9.如图,在中,点、分别在边,上,,,,则的长为 .
10.如图,在和中,,,则的度数为 .
11.在直角梯形中,,,,,,点P是边上一动点,若与相似,则的长度是 .
12.如图,在中,,,为边上的一点,且.若的面积为1,则的面积为 .
13.如图,在中,,,,是上一点,,连接,过作的垂线交于,连接,则 .
14.如图,已知正方形的边在的边上,顶点分别在边上,如果,的面积为12,那么的长为 .
15.如图,将矩形绕点按逆时针方向旋转一定角度后,的对应边交边于点.如果当时量得,,联结、,那么 .
三、解答题
16.如图所示,AB平分∠CAD,∠ABC=∠D=90 .
(1)求证:△ABC∽△ADB;
(2)若AC=6㎝,AD=4㎝,求AB的长.
17.已知:如图,△ABC中,点D、E、F分别在边AB、BC、AC上,且DE∥AC,=.
(1)求证:DF∥BC;
(2)如果DF=2,BE=4,求的值.
18.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
19.如图,矩形ABCD中,AB=4,BC=6,E为线段AD上一动点,连接CE,过点B作BF⊥CE,交射线CD于点F,垂足为P.
(1)求证:CED∽BCF;
(2)当F为CD的中点时,求tan∠BAP的值;
(3)若ABP为等腰三角形时,直接写出DE的长.
20.在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为 ;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是 .(直接给出结论无须证明)
参考答案:
1.D
2.A
3.D
4.B
5.D
6.D
7.C
8.A
9.10
10.40°
11.1或2.8或6
12.3
13.
14.
15.
16.(1)证明:∵AB平分∠CAD ∴∠CAB=∠BAD
∵∠ABC=∠D=90 ∴△ABC∽△ADB
(2)由(1)得△ABC∽△ADB
∴ ,即AB2=AC AD
∴
17.(1)证明:∵DE∥AC,
∴=,
又∵=.
∴=,
∴DF∥BC;
(2)∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,
∴CE=DF=2,
∵BE=4,
∴BC=4+2=6,
∵DF∥BC,
∴,
∴=.
18.解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB10cm;
分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t;
∴t=1或时,△BPQ∽△BCA;
(2)分三种情况:
①当PB=PQ时,如图,过P作PH⊥BQ,
则BHBQ=4﹣2t,PB=5t,
∴PH∥AC,
∴,即解得:t;
②当PB=BQ时,即5t=8﹣4t,
解得:t;
③当BQ=PQ时,如图,过Q作QG⊥AB于G,
则BGPBt,BQ=8﹣4t,
∵,,
∴,
∴即,
解得:t;
综上所述:△BPQ是等腰三角形时t的值为:或或;
(3)如图,过P作PM⊥BC于点M,则PB=5t,
∵AC⊥BC,,
∴,
∴△PMB∽△ACB,
∴,
∴PM=3t,MC=8﹣4t,CQ=4t,
根据勾股定理得,CP2=PM2+MC2=25t2﹣64t+64,
∵CP=CQ,
∴25t2﹣64t+64=16t2,
∴t(不符题意,舍去)或t,
∴CP=CQ时,t;
(4)如图,过P作PM⊥BC于点M,AQ,CP交于点N,
由(3)可知,PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t.
19.(1)∵四边形是矩形,
,
,
,
,
.
(2)如图1,
过点作于点,交于点,
,
,
,
,
;
,
,
,
解得,
,
∴四边形是矩形,
,
,
,
,
,
解得,
,
,
,
解得,
,
(3)当时,如图2,
作于点H,则AH=BH,
,
,
,
,
,
,
∴AE,
∴DE=;
当PA=AB时,如图3,
作AM⊥BP于点M,则,
,
,
,
,
,
,
∴整理得CF,
,
,
;
当BP=AB=4时,如图4,
则,
,
,
.
综上所述,DE的长为或3或.
20.(1)解:∵ΔABC是等边三角形,D是BC边的中点,
∴∠BAD=30°,
∵线段AD和AE关于直线AB对称,
∴DE⊥AB,
∴∠ADE+∠BAD=90°,
∴∠ADE=60°,
∴∠BDE=90°-60°=30°;
故答案为:30°
(2)解:解:①作图如下:
②如图,连接AE.
为等边三角形,
∴∠DAE=60°,AD=AE,
为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,
∴∠BAE=∠CAD,
,
;
(3)解: 如图,连接AE,
∵AC=kBC,AD=kDE,
∴,即,
∵∠ADE=∠C,
∴△ADE∽△ACB,
∴∠AED=∠ABC,∠EAD=∠BAC,
∴∠EAB=∠DAC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AED=∠ADE,
∴AE=AD,
∴△AEB≌△ADC,
∴CD=BE;
∵BC=BD+CD,
∴BC=BD+BE,
∵AC=kBC,
∴k(BE+BD)=AC.
