1.2等腰三角形(二)等腰三角形的性质
文档属性
| 名称 | 1.2等腰三角形(二)等腰三角形的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 367.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-02 00:00:00 | ||
图片预览



文档简介
课件14张PPT。第一节 等腰三角形(二)第一章 三角形的证明兴宁市大坪中学 练小盛想一想, 做一做 在等腰三角形中作出一些线段(如角平分线、中线、高等),你能发现其中一些相等的线段吗? 你能证明你的结论吗? 作图观察,我们可以发现:等腰三角形两底角的平分线相等;两腰上的高、中线也分别相等. 我们知道,观察或度量是不够的,感觉不可靠.这就需要以公理和已证明的定理为基础去证明它,让人们坚定不移地去承认它,相信它.
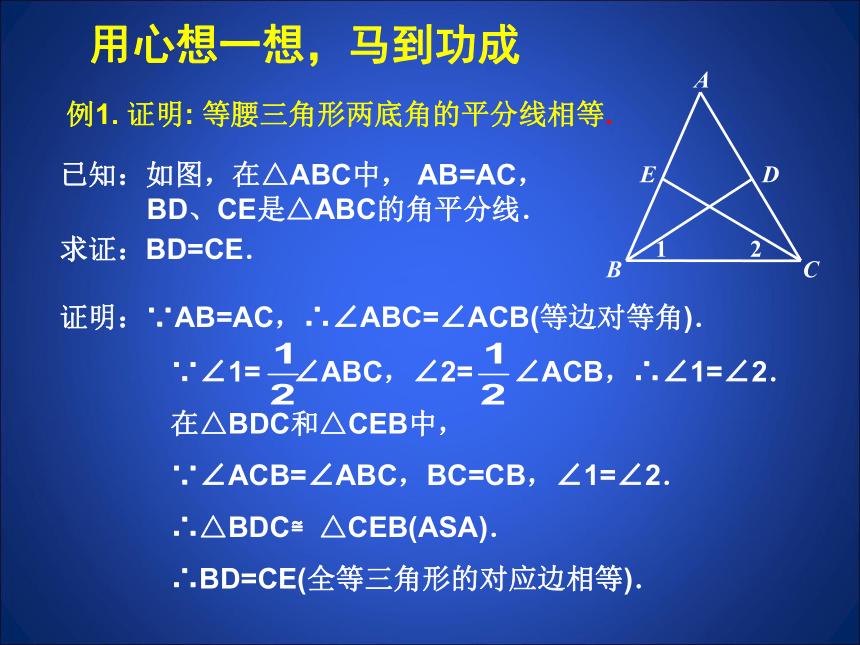
下面我们就来证明上面提到的线段中的一种:等腰三角形两底角的平分线相等.已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.例1. 证明: 等腰三角形两底角的平分线相等.用心想一想,马到功成求证:BD=CE.已知:如图,在△ABC中, AB=AC,
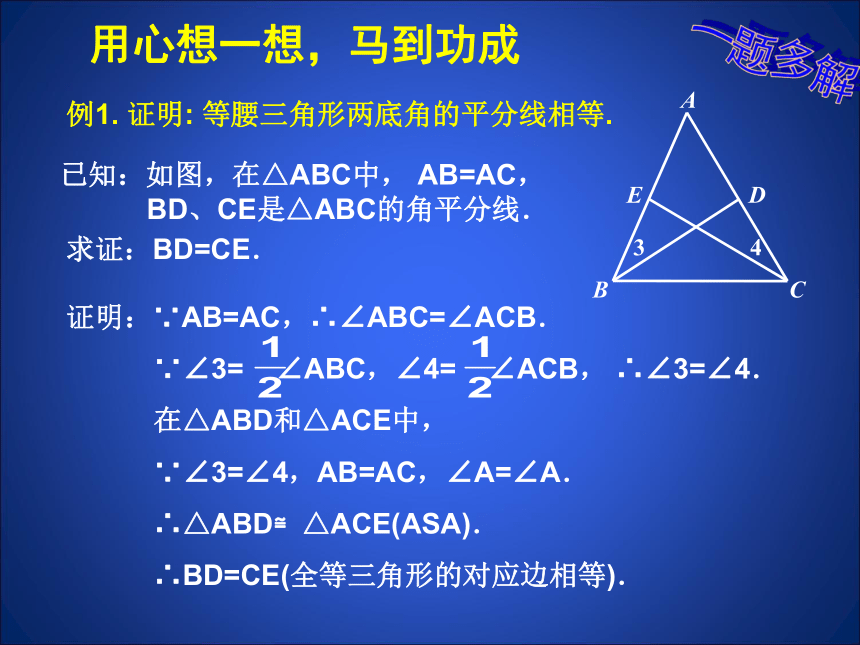
BD、CE是△ABC的角平分线.例1. 证明: 等腰三角形两底角的平分线相等.用心想一想,马到功成求证:BD=CE.一题多解大胆尝试,练一练!已知:如图,在△ABC中, AB=AC,
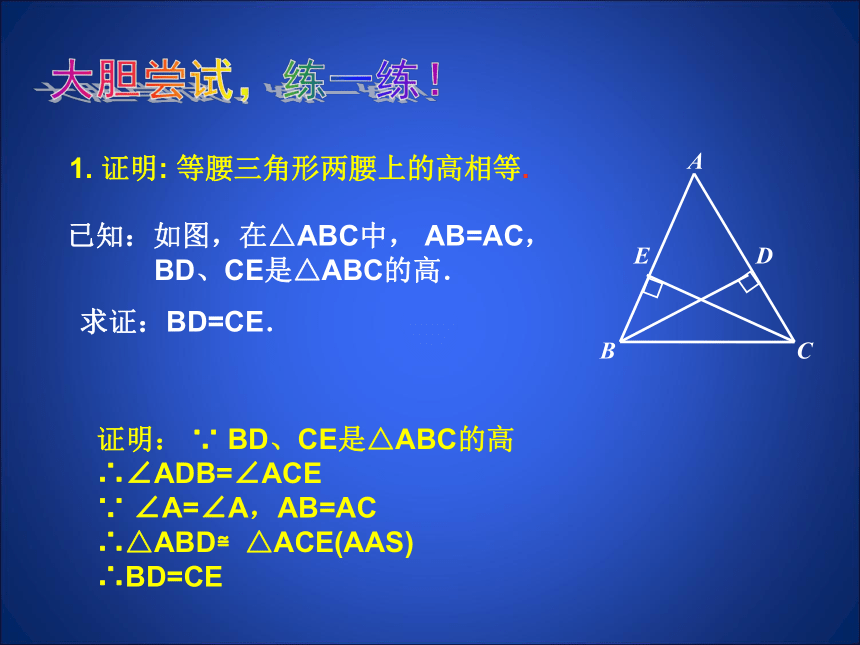
BD、CE是△ABC的高.1. 证明: 等腰三角形两腰上的高相等.求证:BD=CE.证明: ∵ BD、CE是△ABC的高
∴∠ADB=∠ACE
∵ ∠A=∠A,AB=AC
∴△ABD≌△ACE(AAS)
∴BD=CE大胆尝试,练一练!已知:如图,在△ABC中, AB=AC,
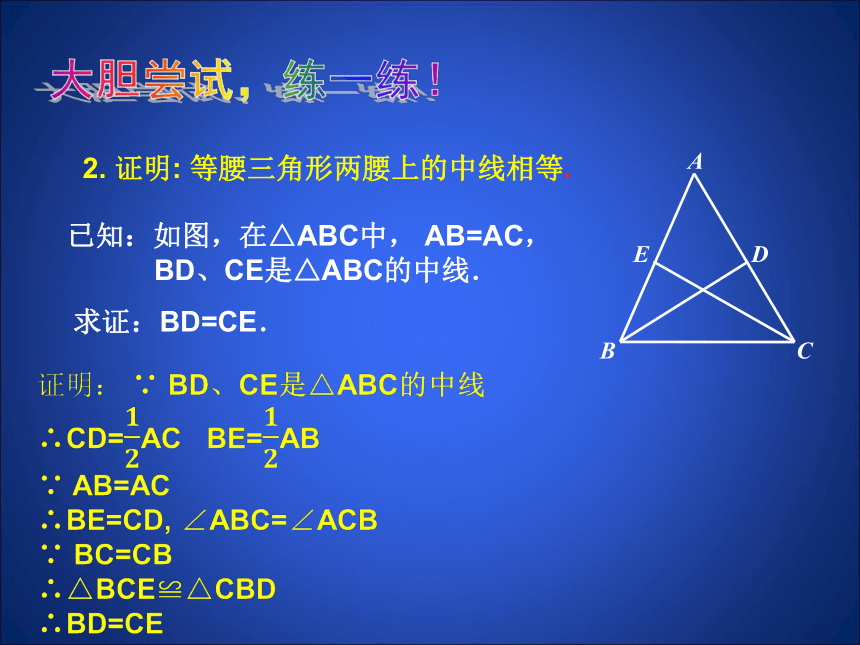
BD、CE是△ABC的中线.2. 证明: 等腰三角形两腰上的中线相等.求证:BD=CE. ? 刚才,我们只是发现并证明了等腰三角形中比较特殊的线段(角平分线、中线、高)相等,还有其他的结论吗?你能从上述证明的过程中得到什么启示?
把腰二等分的线段相等,把底角二等分的线段相等.如果是三等分、四等分……结果如何呢?想一想, 做一做议一议小结 简述为:
(1)在△ABC中,如果AB=AC,∠ABD=∠ACE,那么BD=CE.
(2)在△ABC中,如果AB=AC,AD=AE,那么BD=CE.1. 求证:等边三角形三个内角都相等并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理:∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.大胆尝试,练一练!随堂练习 及时巩固如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD.将不全等的两个等边三角形△ABC和等边三角形△DEF任意摆放,请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的一条直线上有且只有三个顶点(重合的顶点算一个),并说明理由.ABCFE课时小结 1.等腰三角形中还有那些相等的线段?
2.等边三角形有哪些性质?
3.本节课你学到的探索问题的方法是什么? 作业
1.习题1.2 2 3
2.复习本节课知识并预习下一节的内容
下面我们就来证明上面提到的线段中的一种:等腰三角形两底角的平分线相等.已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.例1. 证明: 等腰三角形两底角的平分线相等.用心想一想,马到功成求证:BD=CE.已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.例1. 证明: 等腰三角形两底角的平分线相等.用心想一想,马到功成求证:BD=CE.一题多解大胆尝试,练一练!已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高.1. 证明: 等腰三角形两腰上的高相等.求证:BD=CE.证明: ∵ BD、CE是△ABC的高
∴∠ADB=∠ACE
∵ ∠A=∠A,AB=AC
∴△ABD≌△ACE(AAS)
∴BD=CE大胆尝试,练一练!已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.2. 证明: 等腰三角形两腰上的中线相等.求证:BD=CE. ? 刚才,我们只是发现并证明了等腰三角形中比较特殊的线段(角平分线、中线、高)相等,还有其他的结论吗?你能从上述证明的过程中得到什么启示?
把腰二等分的线段相等,把底角二等分的线段相等.如果是三等分、四等分……结果如何呢?想一想, 做一做议一议小结 简述为:
(1)在△ABC中,如果AB=AC,∠ABD=∠ACE,那么BD=CE.
(2)在△ABC中,如果AB=AC,AD=AE,那么BD=CE.1. 求证:等边三角形三个内角都相等并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理:∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.大胆尝试,练一练!随堂练习 及时巩固如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD.将不全等的两个等边三角形△ABC和等边三角形△DEF任意摆放,请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的一条直线上有且只有三个顶点(重合的顶点算一个),并说明理由.ABCFE课时小结 1.等腰三角形中还有那些相等的线段?
2.等边三角形有哪些性质?
3.本节课你学到的探索问题的方法是什么? 作业
1.习题1.2 2 3
2.复习本节课知识并预习下一节的内容
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
