4.1 科学探究:力的合成 课件(共27张PPT) 2024-2025学年高一物理鲁科版(2019)必修第一册
文档属性
| 名称 | 4.1 科学探究:力的合成 课件(共27张PPT) 2024-2025学年高一物理鲁科版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第1节 科学探究:力的合成
第四章 力与平衡
学习目标
1.知道合力、分力和力的合成的概念。
2.能完成“探究两个互成角度的力的合成规律”的实验。
3.知道力的平行四边形定则,知道矢量和标量遵循不同的运算法则。
4.会用图解法和计算法求共点力的合力。
这两种情形中手对购物篮的作用力不同。
这些力之间有什么关系呢?
两个人可将购物篮提起使其处于静止状态
一个人也可将这个购物篮提起使其处于同样状态
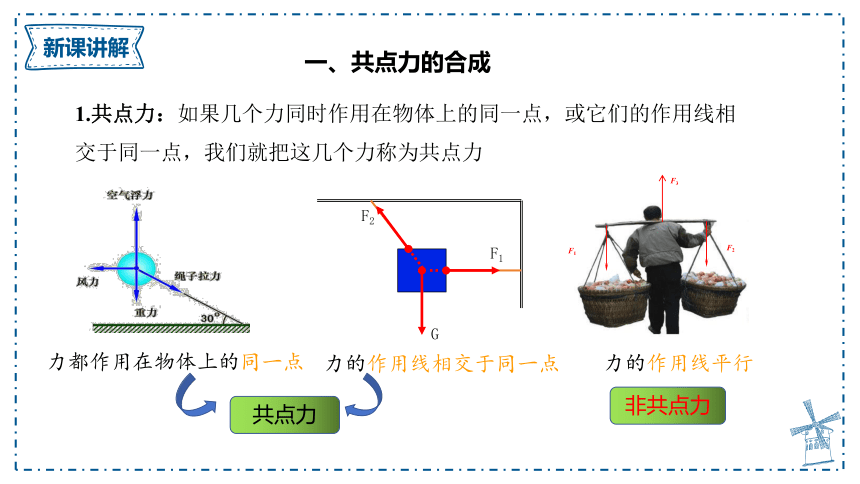
1.共点力:如果几个力同时作用在物体上的同一点,或它们的作用线相交于同一点,我们就把这几个力称为共点力
力都作用在物体上的同一点
G
F1
F2
力的作用线相交于同一点
共点力
F1
F2
F3
力的作用线平行
非共点力
一、共点力的合成
两个人可将购物篮提起使其处于静止状态
一个人也可将这个购物篮提起使其处于同样状态
这两种情形中手对购物篮的作用力不同
但购物篮的状态相同
说明一个人提和两个人提所产生的效果相同
图中F的作用效果与F1、F2共同作用的效果相同
说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
2.合力与分力
(1)定义:一个力产生的效果跟几个力共同作用产生的效果相同,就把这个力F称为那几个力的合力,那几个力则称为个力F的分力。
(2)关系: “等效替代”
3.力的合成
求几个力的合力的过程或求合力的方法叫力的合成。
注意:合力与其分力不能同时作用在物体上。
(多选)关于两个大小不变的力F1、F2及它们的合力F,下列说法正确的是( )
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同一个物体受到的力
C.两力F1、F2与F是物体同时受到的三个力
D.F一定不随F1、F2的变化而变化
AB
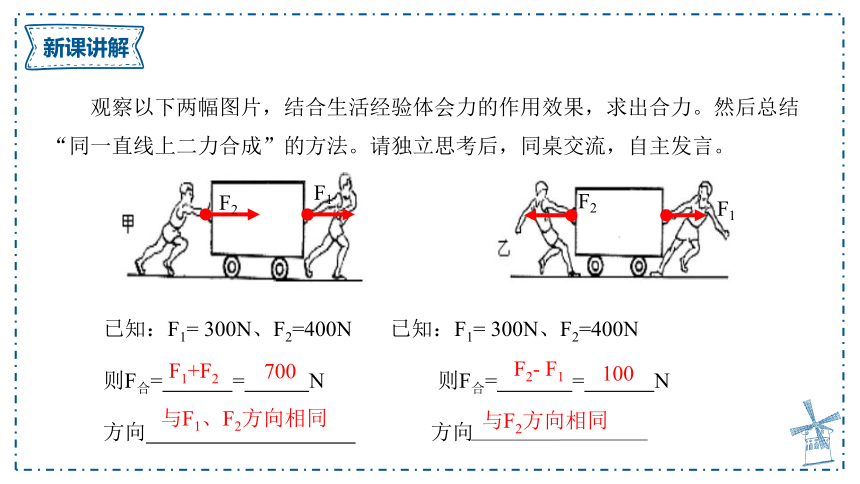
观察以下两幅图片,结合生活经验体会力的作用效果,求出合力。然后总结“同一直线上二力合成”的方法。请独立思考后,同桌交流,自主发言。
已知:F1= 300N、F2=400N 已知:F1= 300N、F2=400N
则F合= = N 则F合= = N
方向 方向
700
F2- F1
F1+F2
100
与F1、F2方向相同
与F2方向相同
F1
F2
F1
F2
同一直线上的二力合成
使用直接加减的方法
同向相加
反向相减
互成角度的两个共点力合成时遵循什么规律?
F合= ?
F1
F2
F2
F1
F
O
F1
F2
F
O
二、探究两个互成角度的力的合成规律
(1)力的作用效果有哪些?
(2)怎样设计才能在判断“合力和分力产生的效果相同”上比较准、比较容易?
---改变物体运动状态、产生形变
---用“形变相同”来反映“效果相同”比较容易且准确
【设计实验】
【实验器材】
木板、橡皮筋、细线、弹簧测力计、图钉、白纸、铅笔、刻度尺、三角板
【实验原理与设计】
让两个互成角度的共点力F1和F2作用于某一物体,并产生明显的作用效果;然后用一个力F来代替F1和F2,产生同样的作用效果。测出F1、F2和F,比较他们的大小和方向,找出其中的规律。
用两个弹簧秤分别钩住细绳套,互成角度地拉橡皮筋,使橡皮筋的结点伸长到某一位置O,记录结点O的位置、两细绳的方向、两弹簧秤的示数F1 、F2 。
只用一只弹簧秤通过细绳套把橡皮筋的结点拉长到同一位置O,记录细绳的方向、弹簧秤的示数F 。
选定一个合适的标度,用力的图示法画出F1、F2和F的图示。
a.拉力不宜过小,两分力夹角稍大点,方便作图。
b. 实验时测力计、橡皮条、细绳应与纸面平行。
c.读数时眼睛应平视弹簧测力计。
F1=1.5N
F2=2N
F=3.2N
F’=3.4N
在误差允许范围内对角线与合力重合,即对角线就表示F1、F2的合力。
根据图示法画出的结果,将F1、F2和F的箭头端用虚线连起来,找出F1、F2和F三者的规律。
【数据分析】
F是F1和F2的合力,F1、F2和F满足平行四边形定则关系。
【实验结论】
如图所示,在研究共点力的合成实验中,以下操作不必要的是( )
A.弹簧测力计使用前调零
B.互成角度拉橡皮筋时两弹簧测力计示数保持相等
C.把橡皮筋的结点拉到同一位置
D.弹簧测力计与木板平面保持平行
B
1.定义:以表示互成角度的两共点力的有向线段为邻边作平行四边形,则两邻边间的对角线所对应的这条有向线段就表示这两个共点力的合力的大小和方向。
F1
F2
o
F
力——实线
辅助线——虚线
三、平行四边形定则
所有矢量的合成都遵守平行四边形定则
注意:平行四边形定则,只适用于共点力!!
2.多个共点力的合力:可用平行四边形定则先求出其中两个力的合力,然后用平行四边形定则再求这个合力与第三个力的合力,直到把所有外力都合成为止,最后得到这些力的合力。
F2
F1
F
F12
F3
O
3.三角形定则
求共点力时,也可以不必完成平行四边形,而是只用它的一半——用一个三角形代替,称为三角形法.如图所示,把两个力首尾相接,连接始端和末端的有向线段即表示它们的合力.
F1
F2
F
F1
F
F2
如果物体受两个以上的力的作用,仍然可以用同样的作图法。
F2
F1
F3
O
F2
F1
F3
O
F
F
如图所示,表示五个共点力的有向线段恰好构成正六边形的两条邻边和三条对角线。已知F1=10 N,则这五个共点力的合力大小为( )
A.0
B.30 N
C.60 N
D.90 N
C
2.合力与分力之间的大小及方向关系
(1)当二分力同向即分力夹角θ=0°时,其合力最大为F=F1+F2(合力与分力同向)
(2)当二分力反向即θ=180°时,其合力最小为F=|F1-F2|(与分力中较大的力同向)
(3)二分力大小不变时其合力大小将随二分力夹角θ增大而减小(θ在0到180之间)
(4)合力方向与分力方向可相同、相反、垂直、或成任意夹角
大小不变的二力合力取值范围|F1-F2|≤F≤ F1+F2
F合可能大于、等于、小于任一分力
总之:合力与分力的大小、方向间无因果关系
1.大小分别为5N、7N、9N的三个力合成,其合力F大小的范围为( )
A. 2N≤F≤20N
B. 3N≤F≤21N
C. 0≤F≤20N
D. 0≤F≤21N
D
2.(多选)已知两共点力F1和F2合力大小为2 N,则下列几组数据可能正确的是 ( )
A.F1=6 N,F2=3 N
B.F1=3 N,F2=3 N
C.F1=2 N,F2=4 N
D.F1=5 N,F2=1 N
BC
【例题】岸边两人同时用力拉小船,两力的大小和方向如图所示。请分别用作图法和计算法求出这两个力的合力。
(1)作图法
选定合适的标度,如用5.0mm长的线段表示150N的力,用0点代表船。依据题意作出力的平行四边形,如图所示。用刻度尺量出表示合力F的对角线长为20.0 mm,可求得合力的大小
用量角器量出F与F1的夹角为60°。
故这两个力的合力大小为600N,方向与F1成60°。
(2)计算法
如图所示,平行四边形的对角线AB、OD交于C点,由于OA=OB,所以平行四边形OADB是菱形,OD与AB互相垂直平分,OD是∠AOB的角平分线,则∠AOD = 60°,OD = 2OC = 2OA cos 60°
因此,合力的大小
F= 2F1cos 60°= 600 N
方向与F1成60°。
等效替代
第1节 科学探究:力的合成
第四章 力与平衡
学习目标
1.知道合力、分力和力的合成的概念。
2.能完成“探究两个互成角度的力的合成规律”的实验。
3.知道力的平行四边形定则,知道矢量和标量遵循不同的运算法则。
4.会用图解法和计算法求共点力的合力。
这两种情形中手对购物篮的作用力不同。
这些力之间有什么关系呢?
两个人可将购物篮提起使其处于静止状态
一个人也可将这个购物篮提起使其处于同样状态
1.共点力:如果几个力同时作用在物体上的同一点,或它们的作用线相交于同一点,我们就把这几个力称为共点力
力都作用在物体上的同一点
G
F1
F2
力的作用线相交于同一点
共点力
F1
F2
F3
力的作用线平行
非共点力
一、共点力的合成
两个人可将购物篮提起使其处于静止状态
一个人也可将这个购物篮提起使其处于同样状态
这两种情形中手对购物篮的作用力不同
但购物篮的状态相同
说明一个人提和两个人提所产生的效果相同
图中F的作用效果与F1、F2共同作用的效果相同
说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
2.合力与分力
(1)定义:一个力产生的效果跟几个力共同作用产生的效果相同,就把这个力F称为那几个力的合力,那几个力则称为个力F的分力。
(2)关系: “等效替代”
3.力的合成
求几个力的合力的过程或求合力的方法叫力的合成。
注意:合力与其分力不能同时作用在物体上。
(多选)关于两个大小不变的力F1、F2及它们的合力F,下列说法正确的是( )
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同一个物体受到的力
C.两力F1、F2与F是物体同时受到的三个力
D.F一定不随F1、F2的变化而变化
AB
观察以下两幅图片,结合生活经验体会力的作用效果,求出合力。然后总结“同一直线上二力合成”的方法。请独立思考后,同桌交流,自主发言。
已知:F1= 300N、F2=400N 已知:F1= 300N、F2=400N
则F合= = N 则F合= = N
方向 方向
700
F2- F1
F1+F2
100
与F1、F2方向相同
与F2方向相同
F1
F2
F1
F2
同一直线上的二力合成
使用直接加减的方法
同向相加
反向相减
互成角度的两个共点力合成时遵循什么规律?
F合= ?
F1
F2
F2
F1
F
O
F1
F2
F
O
二、探究两个互成角度的力的合成规律
(1)力的作用效果有哪些?
(2)怎样设计才能在判断“合力和分力产生的效果相同”上比较准、比较容易?
---改变物体运动状态、产生形变
---用“形变相同”来反映“效果相同”比较容易且准确
【设计实验】
【实验器材】
木板、橡皮筋、细线、弹簧测力计、图钉、白纸、铅笔、刻度尺、三角板
【实验原理与设计】
让两个互成角度的共点力F1和F2作用于某一物体,并产生明显的作用效果;然后用一个力F来代替F1和F2,产生同样的作用效果。测出F1、F2和F,比较他们的大小和方向,找出其中的规律。
用两个弹簧秤分别钩住细绳套,互成角度地拉橡皮筋,使橡皮筋的结点伸长到某一位置O,记录结点O的位置、两细绳的方向、两弹簧秤的示数F1 、F2 。
只用一只弹簧秤通过细绳套把橡皮筋的结点拉长到同一位置O,记录细绳的方向、弹簧秤的示数F 。
选定一个合适的标度,用力的图示法画出F1、F2和F的图示。
a.拉力不宜过小,两分力夹角稍大点,方便作图。
b. 实验时测力计、橡皮条、细绳应与纸面平行。
c.读数时眼睛应平视弹簧测力计。
F1=1.5N
F2=2N
F=3.2N
F’=3.4N
在误差允许范围内对角线与合力重合,即对角线就表示F1、F2的合力。
根据图示法画出的结果,将F1、F2和F的箭头端用虚线连起来,找出F1、F2和F三者的规律。
【数据分析】
F是F1和F2的合力,F1、F2和F满足平行四边形定则关系。
【实验结论】
如图所示,在研究共点力的合成实验中,以下操作不必要的是( )
A.弹簧测力计使用前调零
B.互成角度拉橡皮筋时两弹簧测力计示数保持相等
C.把橡皮筋的结点拉到同一位置
D.弹簧测力计与木板平面保持平行
B
1.定义:以表示互成角度的两共点力的有向线段为邻边作平行四边形,则两邻边间的对角线所对应的这条有向线段就表示这两个共点力的合力的大小和方向。
F1
F2
o
F
力——实线
辅助线——虚线
三、平行四边形定则
所有矢量的合成都遵守平行四边形定则
注意:平行四边形定则,只适用于共点力!!
2.多个共点力的合力:可用平行四边形定则先求出其中两个力的合力,然后用平行四边形定则再求这个合力与第三个力的合力,直到把所有外力都合成为止,最后得到这些力的合力。
F2
F1
F
F12
F3
O
3.三角形定则
求共点力时,也可以不必完成平行四边形,而是只用它的一半——用一个三角形代替,称为三角形法.如图所示,把两个力首尾相接,连接始端和末端的有向线段即表示它们的合力.
F1
F2
F
F1
F
F2
如果物体受两个以上的力的作用,仍然可以用同样的作图法。
F2
F1
F3
O
F2
F1
F3
O
F
F
如图所示,表示五个共点力的有向线段恰好构成正六边形的两条邻边和三条对角线。已知F1=10 N,则这五个共点力的合力大小为( )
A.0
B.30 N
C.60 N
D.90 N
C
2.合力与分力之间的大小及方向关系
(1)当二分力同向即分力夹角θ=0°时,其合力最大为F=F1+F2(合力与分力同向)
(2)当二分力反向即θ=180°时,其合力最小为F=|F1-F2|(与分力中较大的力同向)
(3)二分力大小不变时其合力大小将随二分力夹角θ增大而减小(θ在0到180之间)
(4)合力方向与分力方向可相同、相反、垂直、或成任意夹角
大小不变的二力合力取值范围|F1-F2|≤F≤ F1+F2
F合可能大于、等于、小于任一分力
总之:合力与分力的大小、方向间无因果关系
1.大小分别为5N、7N、9N的三个力合成,其合力F大小的范围为( )
A. 2N≤F≤20N
B. 3N≤F≤21N
C. 0≤F≤20N
D. 0≤F≤21N
D
2.(多选)已知两共点力F1和F2合力大小为2 N,则下列几组数据可能正确的是 ( )
A.F1=6 N,F2=3 N
B.F1=3 N,F2=3 N
C.F1=2 N,F2=4 N
D.F1=5 N,F2=1 N
BC
【例题】岸边两人同时用力拉小船,两力的大小和方向如图所示。请分别用作图法和计算法求出这两个力的合力。
(1)作图法
选定合适的标度,如用5.0mm长的线段表示150N的力,用0点代表船。依据题意作出力的平行四边形,如图所示。用刻度尺量出表示合力F的对角线长为20.0 mm,可求得合力的大小
用量角器量出F与F1的夹角为60°。
故这两个力的合力大小为600N,方向与F1成60°。
(2)计算法
如图所示,平行四边形的对角线AB、OD交于C点,由于OA=OB,所以平行四边形OADB是菱形,OD与AB互相垂直平分,OD是∠AOB的角平分线,则∠AOD = 60°,OD = 2OC = 2OA cos 60°
因此,合力的大小
F= 2F1cos 60°= 600 N
方向与F1成60°。
等效替代
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
