4.2 力的分解 课件 (共21张PPT)2024-2025学年高一物理鲁科版(2019)必修第一册
文档属性
| 名称 | 4.2 力的分解 课件 (共21张PPT)2024-2025学年高一物理鲁科版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第1节 力的分解
第四章 力与平衡
学习目标
1.知道力的分解,知道力的分解是力的合成的逆运算,遵循平行四边形定则。
2.能正确应用正交分解法对力进行分解。
3.会用力的分解解决生活实际问题,知道力的分解在生活中的应用。
为拉出深陷泥坑的汽车,可将绳子的一端绑在树上,另一端和汽车相连,并使绳子绷紧,然后在绳子中间用垂直于绳子的较小的力拉绳,就可把汽车拉出。
给你一根绳子,你能把深陷泥坑的汽车拉出么?
F
你能说明其中的道理么?
F
F1
F2
F
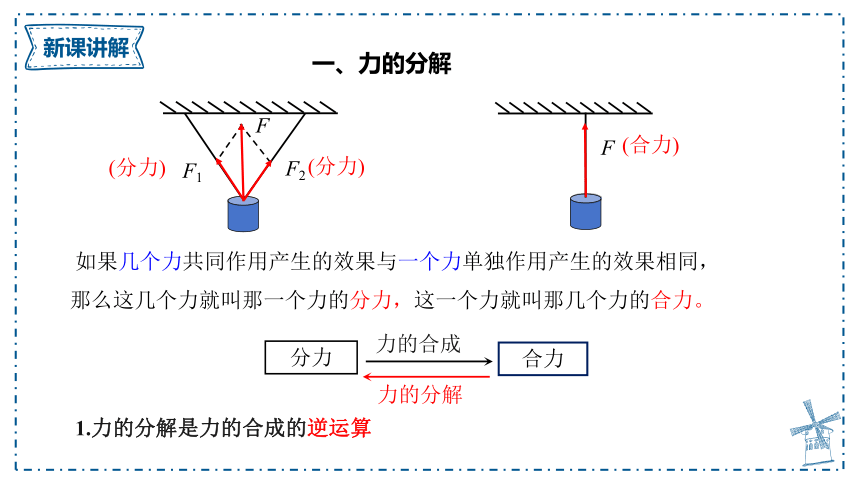
如果几个力共同作用产生的效果与一个力单独作用产生的效果相同,那么这几个力就叫那一个力的分力,这一个力就叫那几个力的合力。
(分力)
(分力)
(合力)
力的合成
力的分解
分力
合力
1.力的分解是力的合成的逆运算
一、力的分解
F
F1
F2
2.力的分解同样遵守平行四边行定则
力F为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力。
一个力F可以有多少组分力?
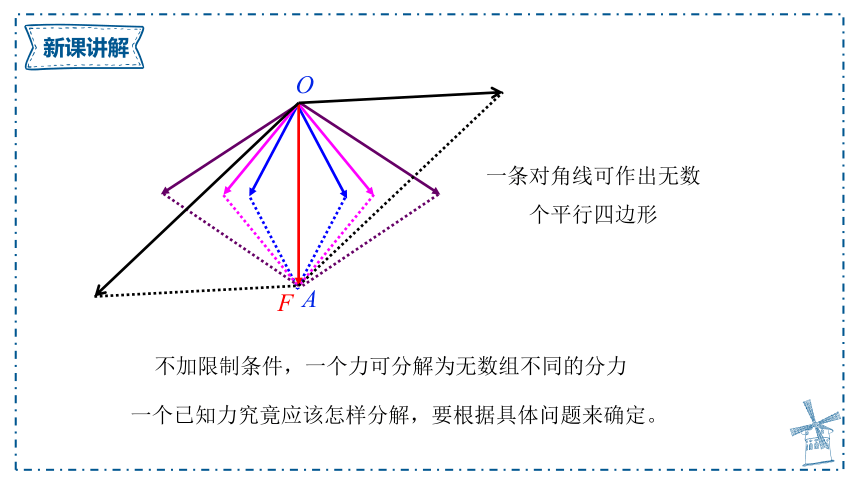
一条对角线可作出无数个平行四边形
不加限制条件,一个力可分解为无数组不同的分力
A
F
O
一个已知力究竟应该怎样分解,要根据具体问题来确定。
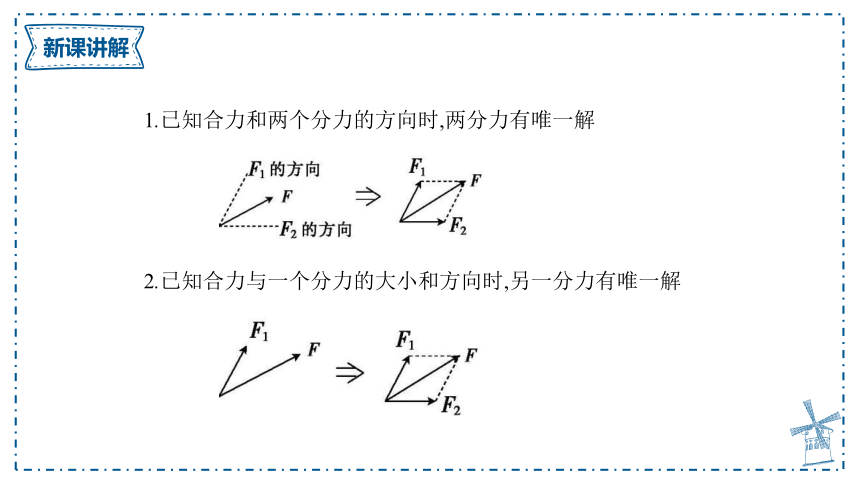
1.已知合力和两个分力的方向时,两分力有唯一解
2.已知合力与一个分力的大小和方向时,另一分力有唯一解
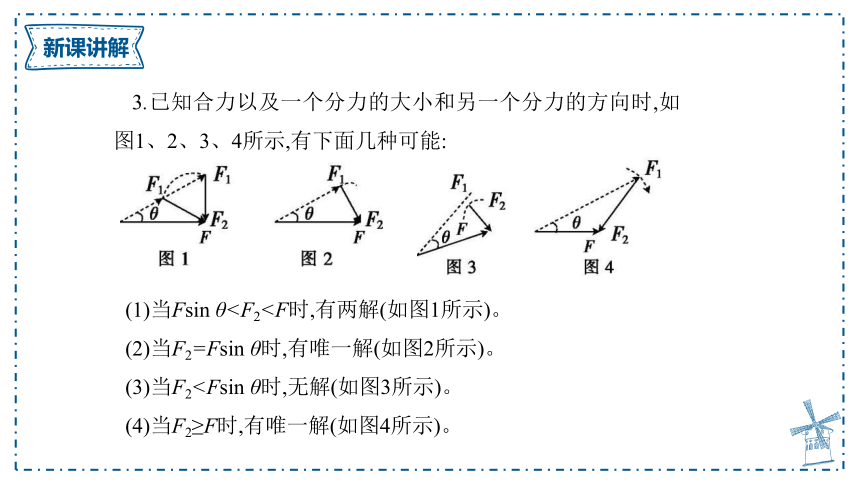
3.已知合力以及一个分力的大小和另一个分力的方向时,如图1、2、3、4所示,有下面几种可能:
(1)当Fsin θ(2)当F2=Fsin θ时,有唯一解(如图2所示)。
(3)当F2(4)当F2≥F时,有唯一解(如图4所示)。
如图所示,将一个力F=10N分解为两个分力,已知一个分力F1的方向与F成30°角,另一个分力F2的大小为6N,则在该力的分解中( )
A.有唯一解
B.有两组解
C.有无数组解
D.无解
F
30°
B
二、力的正交分解
F
Fx
Fy
拉力效果一:水平向前拉箱子
拉力效果二:竖直向上提箱子
θ
θ
G2
G1
G
重力效果一:使物体沿斜面下滑
重力效果二:使物体压紧斜面
正交分解:把一个力分解为两个相互垂直的分力的过程
1.选择一个坐标轴,将力分解为两个轴上的相互垂直的分力
F
O
y
x
Fx
Fy
Fx=Fcosθ
Fy=Fsinθ
2.求F1、F2、F3、F4这四个力的合力
F1
F2
F3
F4
O
计算复杂
如何更简单、更有效的求解多个力的合力?
计算法
F1
F2
F3
F4
O
x
y
α
β
F4y
F4x
F3x
F3y
正交分解法
①建立直角坐标系。以共点力的作用点为原点,以水平方向或物体运动的方向为x轴(使尽量多的力在坐标轴上)
②正交分解各力。将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。
Fx=F1-F4x-F3x=F1-F4cosα-F3cosβ;
Fy=F2+F3y-F4y=F2+F3sinα+F4sinβ;
F1
F2
F3
F4
O
x
y
α
β
F4y
F4x
F3x
F3y
多个力合成时,正交分解法可以更有效地进行合成
如图所示,已知共面的三个力F1=20 N、F2=30 N、F3=40 N,作用于物体的同一点上,三个力两两之间的夹角都是120°,求合力的大小和方向。
答案:,
合力方向与F3方向所成夹角为30°
F
F
F2
F1
F1
F2
为什么用一根绳子就能把深陷泥坑的汽车拉出来?
三、力的分解的应用
施加的较小的力可在绳子上分解成较大的两个力,使绳对车产生很大的拉力,从而把汽车拉出。
在一只带把手的杯子里加半杯水,用一根橡皮筋水平拉着,直到把杯子拉动,感受两手用力的大小。当两根橡皮筋之间的夹角增大时,同样拉动杯子,你感觉两手所用的力是增大了还是减小了?
分力大小与夹角的关系
合力一定,两等大分力随它们之间夹角的增大而增大
在我国古代,智慧的劳动人民就利用合力与分力的关系,设计出了结构精美的拱桥,大大提高了桥梁的承载能力
盘山公路
斧刃越薄越好
假期里,一位同学在厨房里协助妈妈做菜,对菜刀产生了兴趣。他发现菜刀的刀刃前部和后部的厚薄不一样,如图所示,菜刀横截面为等腰三角形,刀刃前部的横截面顶角较小,后部的顶角较大,他先后做出过几个猜想,其中合理的是( )
A.刀刃前部和后部厚薄不匀,仅是为了打造方便、外形美观,跟使用功能无关
B.在刀背上加上同样的压力时,分开其他物体的力的大小跟刀刃厚薄无关
C.在刀背上加上同样的压力时,顶角越大,分开其他物体的力的大小越大
D.在刀背上加上同样的压力时,顶角越小,分开其他物体的力的大小越大
D
第1节 力的分解
第四章 力与平衡
学习目标
1.知道力的分解,知道力的分解是力的合成的逆运算,遵循平行四边形定则。
2.能正确应用正交分解法对力进行分解。
3.会用力的分解解决生活实际问题,知道力的分解在生活中的应用。
为拉出深陷泥坑的汽车,可将绳子的一端绑在树上,另一端和汽车相连,并使绳子绷紧,然后在绳子中间用垂直于绳子的较小的力拉绳,就可把汽车拉出。
给你一根绳子,你能把深陷泥坑的汽车拉出么?
F
你能说明其中的道理么?
F
F1
F2
F
如果几个力共同作用产生的效果与一个力单独作用产生的效果相同,那么这几个力就叫那一个力的分力,这一个力就叫那几个力的合力。
(分力)
(分力)
(合力)
力的合成
力的分解
分力
合力
1.力的分解是力的合成的逆运算
一、力的分解
F
F1
F2
2.力的分解同样遵守平行四边行定则
力F为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力。
一个力F可以有多少组分力?
一条对角线可作出无数个平行四边形
不加限制条件,一个力可分解为无数组不同的分力
A
F
O
一个已知力究竟应该怎样分解,要根据具体问题来确定。
1.已知合力和两个分力的方向时,两分力有唯一解
2.已知合力与一个分力的大小和方向时,另一分力有唯一解
3.已知合力以及一个分力的大小和另一个分力的方向时,如图1、2、3、4所示,有下面几种可能:
(1)当Fsin θ
(3)当F2
如图所示,将一个力F=10N分解为两个分力,已知一个分力F1的方向与F成30°角,另一个分力F2的大小为6N,则在该力的分解中( )
A.有唯一解
B.有两组解
C.有无数组解
D.无解
F
30°
B
二、力的正交分解
F
Fx
Fy
拉力效果一:水平向前拉箱子
拉力效果二:竖直向上提箱子
θ
θ
G2
G1
G
重力效果一:使物体沿斜面下滑
重力效果二:使物体压紧斜面
正交分解:把一个力分解为两个相互垂直的分力的过程
1.选择一个坐标轴,将力分解为两个轴上的相互垂直的分力
F
O
y
x
Fx
Fy
Fx=Fcosθ
Fy=Fsinθ
2.求F1、F2、F3、F4这四个力的合力
F1
F2
F3
F4
O
计算复杂
如何更简单、更有效的求解多个力的合力?
计算法
F1
F2
F3
F4
O
x
y
α
β
F4y
F4x
F3x
F3y
正交分解法
①建立直角坐标系。以共点力的作用点为原点,以水平方向或物体运动的方向为x轴(使尽量多的力在坐标轴上)
②正交分解各力。将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。
Fx=F1-F4x-F3x=F1-F4cosα-F3cosβ;
Fy=F2+F3y-F4y=F2+F3sinα+F4sinβ;
F1
F2
F3
F4
O
x
y
α
β
F4y
F4x
F3x
F3y
多个力合成时,正交分解法可以更有效地进行合成
如图所示,已知共面的三个力F1=20 N、F2=30 N、F3=40 N,作用于物体的同一点上,三个力两两之间的夹角都是120°,求合力的大小和方向。
答案:,
合力方向与F3方向所成夹角为30°
F
F
F2
F1
F1
F2
为什么用一根绳子就能把深陷泥坑的汽车拉出来?
三、力的分解的应用
施加的较小的力可在绳子上分解成较大的两个力,使绳对车产生很大的拉力,从而把汽车拉出。
在一只带把手的杯子里加半杯水,用一根橡皮筋水平拉着,直到把杯子拉动,感受两手用力的大小。当两根橡皮筋之间的夹角增大时,同样拉动杯子,你感觉两手所用的力是增大了还是减小了?
分力大小与夹角的关系
合力一定,两等大分力随它们之间夹角的增大而增大
在我国古代,智慧的劳动人民就利用合力与分力的关系,设计出了结构精美的拱桥,大大提高了桥梁的承载能力
盘山公路
斧刃越薄越好
假期里,一位同学在厨房里协助妈妈做菜,对菜刀产生了兴趣。他发现菜刀的刀刃前部和后部的厚薄不一样,如图所示,菜刀横截面为等腰三角形,刀刃前部的横截面顶角较小,后部的顶角较大,他先后做出过几个猜想,其中合理的是( )
A.刀刃前部和后部厚薄不匀,仅是为了打造方便、外形美观,跟使用功能无关
B.在刀背上加上同样的压力时,分开其他物体的力的大小跟刀刃厚薄无关
C.在刀背上加上同样的压力时,顶角越大,分开其他物体的力的大小越大
D.在刀背上加上同样的压力时,顶角越小,分开其他物体的力的大小越大
D
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
