北京市海淀区北京理工大学附属中学2024-2025学年高二上学期10月月考数学试题(含答案)
文档属性
| 名称 | 北京市海淀区北京理工大学附属中学2024-2025学年高二上学期10月月考数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 773.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 20:26:03 | ||
图片预览



文档简介
北京理工大学附属中学2024-2025学年高二上学期10月月考
数学试题
(2024.10)
班级______姓名______学号______
一、选择题(本大题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)
1. 已知点,则点关于轴的对称点的坐标为( )
A B. C. D.
2. 已知向量,,且,那么( )
A. B. 6 C. 9 D. 18
3. 如图,在三棱锥O-ABC中,D是BC的中点,若,,,则等于( )
A. B.
C. D.
4. 已知正四棱锥,底面边长是,体积是,那么这个四棱锥侧棱长为( )
A. B. C. D.
5. 如图,在三棱锥中,,且,E,F分别是棱,的中点,则EF和AC所成的角等于
A. 30° B. 45° C. 60° D. 90°
6. 已知是两条不重合的直线,,,是三个两两不重合的平面,给出下列四个命题:
①若则;
②若则;
③若则;
④若是异面直线,则.其中真命题是( )
A. ①和② B. ①和③ C. ③和④ D. ①和④
7. 在正方体中,直线是底面所在平面内的一条动直线,记直线与直线所成的角为,则的最小值是( )
A. B. C. D.
8. 如图,平行六面体中,,,则( )
A. 1 B. C. 9 D. 3
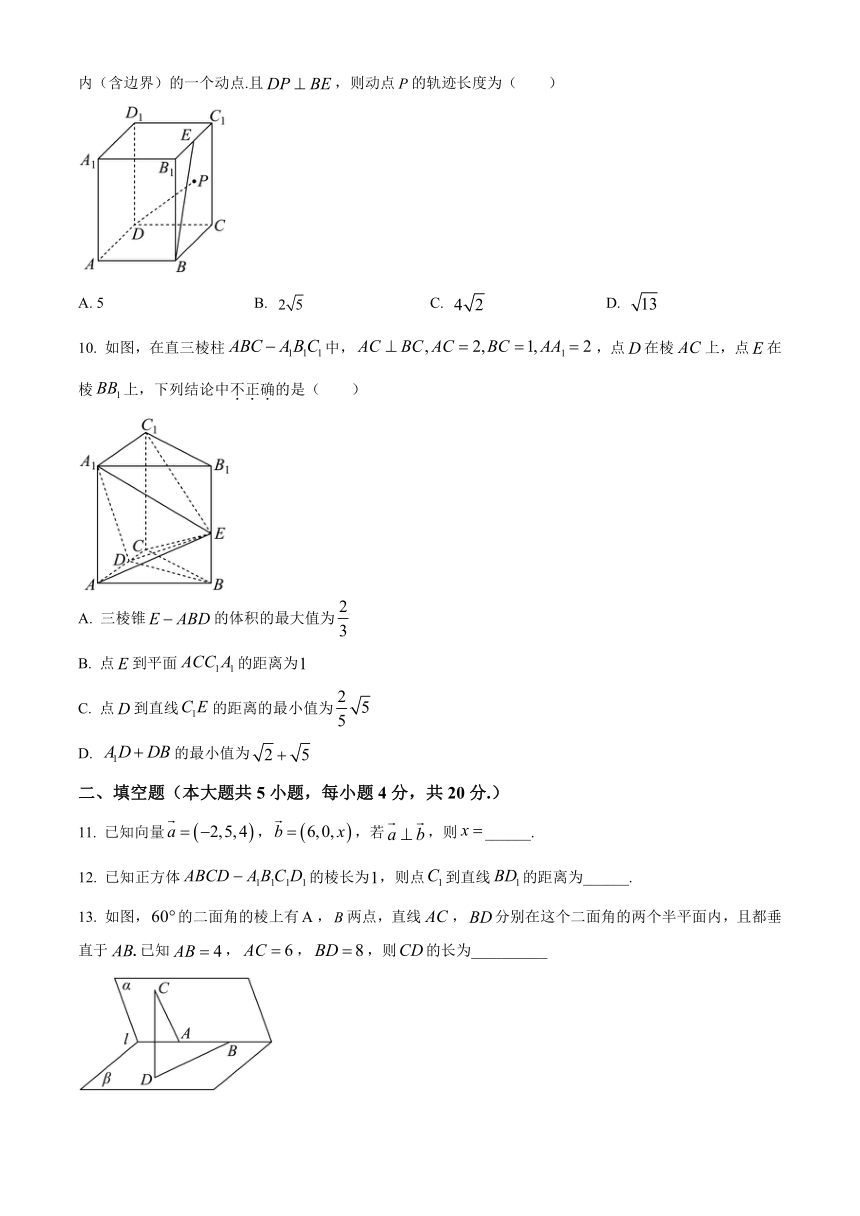
9. 如图,在长方体中,为棱的中点,为四边形内(含边界)的一个动点.且,则动点的轨迹长度为( )
A. 5 B. C. D.
10. 如图,在直三棱柱中,,点在棱上,点在棱上,下列结论中不正确的是( )
A. 三棱锥的体积的最大值为
B. 点到平面的距离为
C. 点到直线的距离的最小值为
D. 的最小值为
二、填空题(本大题共5小题,每小题4分,共20分.)
11. 已知向量,,若,则______.
12. 已知正方体的棱长为,则点到直线的距离为______.
13. 如图,的二面角的棱上有,两点,直线,分别在这个二面角的两个半平面内,且都垂直于已知,,,则的长为__________
14. 在我国古代数学名著《九章算术》中,四个面都为直角三角形的三棱锥称为鳖臑.已知在鳖臑中,平面ABC,.M为PC的中点,则点P到平面MAB的距离为______.
15. 如图,在正方体中,点P在线段上运动,则下列结论正确的是________.
①直线平面
②三棱锥体积为定值
③异面直线AP与所成角的取值范围是
④直线与平面所成角的正弦值的最大值为
三、解答题(本大题共4小题,每小题10分,共40分.解答应写出文字说明、演算步骤或证明过程.)
16. 如图,在四棱锥中,底面是平行四边形,,分别为,中点.
(1)求证:平面;
(2)若,平面,求证:平面.
17. 如图,在直三棱柱中,,、分别为、的中点,.
(1)求证:;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
18. 如图,在四棱锥中,底面是边长为2的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
19. 在梯形中,,,,为的中点,线段与交于点(如图1).将△沿折起到△位置,使得(如图2).
(1)求证:平面平面;
(2)线段上是否存在点,使得与平面所成角的正弦值为 若存在,求出的值;若不存在,请说明理由.
参考答案
1. D.
2. A.
3. C.
4. C
5. B.
6. D.
7. .
8. D.
9. B
10. D.
11. 3.
12. .
13.
14.
15. ①②④
16. (1)证明:连接,
∵四边形是平行四边形,且是的中点,
∴是的中点,
∵E为PC中点,
∴,
∵平面,平面,
∴平面.
(2)证明:∵平面,平面,
∴,
∵,,平面,
∴面,
∵,
∴平面.
17. (1)证明:因为三棱柱是直三棱柱,所以平面,
因为平面,所以,
又因为,为中点,所以,
因为平面,所以平面,
因为平面,所以.
(2)
(3)
18. (1)证明:因为底面是正方形,所以,
平面,平面,
所以平面,
又因为平面与交于点.
平面,平面平面
所以.
(2)
19. (1)证明:∵在梯形中,,
,,为的中点,
∴,,,
∴是正三角形,四边形为菱形,
∴,,
∵,
又∵平面ABC,
∴平面ABC,
∵平面,
∴平面⊥平面ABC.
(2)存在,
数学试题
(2024.10)
班级______姓名______学号______
一、选择题(本大题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)
1. 已知点,则点关于轴的对称点的坐标为( )
A B. C. D.
2. 已知向量,,且,那么( )
A. B. 6 C. 9 D. 18
3. 如图,在三棱锥O-ABC中,D是BC的中点,若,,,则等于( )
A. B.
C. D.
4. 已知正四棱锥,底面边长是,体积是,那么这个四棱锥侧棱长为( )
A. B. C. D.
5. 如图,在三棱锥中,,且,E,F分别是棱,的中点,则EF和AC所成的角等于
A. 30° B. 45° C. 60° D. 90°
6. 已知是两条不重合的直线,,,是三个两两不重合的平面,给出下列四个命题:
①若则;
②若则;
③若则;
④若是异面直线,则.其中真命题是( )
A. ①和② B. ①和③ C. ③和④ D. ①和④
7. 在正方体中,直线是底面所在平面内的一条动直线,记直线与直线所成的角为,则的最小值是( )
A. B. C. D.
8. 如图,平行六面体中,,,则( )
A. 1 B. C. 9 D. 3
9. 如图,在长方体中,为棱的中点,为四边形内(含边界)的一个动点.且,则动点的轨迹长度为( )
A. 5 B. C. D.
10. 如图,在直三棱柱中,,点在棱上,点在棱上,下列结论中不正确的是( )
A. 三棱锥的体积的最大值为
B. 点到平面的距离为
C. 点到直线的距离的最小值为
D. 的最小值为
二、填空题(本大题共5小题,每小题4分,共20分.)
11. 已知向量,,若,则______.
12. 已知正方体的棱长为,则点到直线的距离为______.
13. 如图,的二面角的棱上有,两点,直线,分别在这个二面角的两个半平面内,且都垂直于已知,,,则的长为__________
14. 在我国古代数学名著《九章算术》中,四个面都为直角三角形的三棱锥称为鳖臑.已知在鳖臑中,平面ABC,.M为PC的中点,则点P到平面MAB的距离为______.
15. 如图,在正方体中,点P在线段上运动,则下列结论正确的是________.
①直线平面
②三棱锥体积为定值
③异面直线AP与所成角的取值范围是
④直线与平面所成角的正弦值的最大值为
三、解答题(本大题共4小题,每小题10分,共40分.解答应写出文字说明、演算步骤或证明过程.)
16. 如图,在四棱锥中,底面是平行四边形,,分别为,中点.
(1)求证:平面;
(2)若,平面,求证:平面.
17. 如图,在直三棱柱中,,、分别为、的中点,.
(1)求证:;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
18. 如图,在四棱锥中,底面是边长为2的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
19. 在梯形中,,,,为的中点,线段与交于点(如图1).将△沿折起到△位置,使得(如图2).
(1)求证:平面平面;
(2)线段上是否存在点,使得与平面所成角的正弦值为 若存在,求出的值;若不存在,请说明理由.
参考答案
1. D.
2. A.
3. C.
4. C
5. B.
6. D.
7. .
8. D.
9. B
10. D.
11. 3.
12. .
13.
14.
15. ①②④
16. (1)证明:连接,
∵四边形是平行四边形,且是的中点,
∴是的中点,
∵E为PC中点,
∴,
∵平面,平面,
∴平面.
(2)证明:∵平面,平面,
∴,
∵,,平面,
∴面,
∵,
∴平面.
17. (1)证明:因为三棱柱是直三棱柱,所以平面,
因为平面,所以,
又因为,为中点,所以,
因为平面,所以平面,
因为平面,所以.
(2)
(3)
18. (1)证明:因为底面是正方形,所以,
平面,平面,
所以平面,
又因为平面与交于点.
平面,平面平面
所以.
(2)
19. (1)证明:∵在梯形中,,
,,为的中点,
∴,,,
∴是正三角形,四边形为菱形,
∴,,
∵,
又∵平面ABC,
∴平面ABC,
∵平面,
∴平面⊥平面ABC.
(2)存在,
同课章节目录
