2023-2024学年浙江省湖州市长兴县六年级(上)月考数学试卷(11月份)(含答案)
文档属性
| 名称 | 2023-2024学年浙江省湖州市长兴县六年级(上)月考数学试卷(11月份)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览




文档简介
2023-2024学年浙江省湖州市长兴县六年级(上)月考数学试卷(11月份)
一、填空题。(第6题2分,其他每空1分,共19分)
1.(2分)圆有 条对称轴,扇形有 条对称轴。
2.(2分)一个圆向右滚动后如图,要画一个同样的圆,那么圆规两脚的距离应为 厘米,这个圆的面积是 平方厘米。
3.(2分)如图所示,正方形的四个顶点均在圆上,已知正方形的对角线长8cm,圆的周长是 cm,面积是 cm2。
4.(2分)小圆的直径等于大圆的半径,小圆与大圆的周长的比值是 ,大圆与小圆面积的比是 。
5.(2分)在一个长3分米,宽为2分米的长方形里剪一个最大的圆,圆的面积是 平方分米,剩下部分的面积是 平方分米。
6.(2分)如图,小圆的直径是2厘米。
(1)两个小圆的面积之和是大圆面积的。
(2)两个小圆的周长之和 大圆的周长。(填“大于”“小于”或“等于”)
7.(1分)一个圆形花坛的直径是40m,扩建后,半径增加了10m,这个花坛扩建后的面积增加了 m2。
8.(2分)有一个半圆形的水池,量得它的周长是10.28米,这个水池的半径是 ,面积是 。
9.(2分)将一个直径是4dm的圆等分成若干份剪开,再拼成一个近似的长方形,这个长方形的周长是
dm,面积是 dm2。
10.(2分)如图,大半圆的直径是10cm,小半圆直径是4cm,阴影部分的周长是 cm,面积是 cm2。
二、判断题。(对的画“√”,错的画“×”)(5分)
11.(1分)通过圆心,并且两端都在圆上的线段叫做直径。 .
12.(1分)当圆的半径等于2分米时,这个圆的周长和面积相等。 .
13.(1分)所有圆的周长和它的直径的比值都相等。 .
14.(1分)两个半圆一定可以拼成一个整圆。 .
15.(1分)圆的面积比扇形的面积大。 .
三、选择题。(将正确答案的序号填在括号里)(10分)
16.(2分)下列说法中正确的有( )个。
①圆的半径扩大到原来的2倍,那么周长和面积都扩大到原来的2倍。
②半圆的周长是圆的周长的一半。
③圆心角是90°的扇形的面积是圆的面积的。
④如图,正方形的面积是10cm2,圆的面积是31.4cm2。
A.1 B.2 C.3 D.4
17.(2分)一个圆的直径与一个正方形的边长相等,它们的面积相比( )
A.相等 B.圆大 C.正方形大 D.不确定
18.(2分)一台拖拉机,后轮直径是前轮直径的2倍,后轮转动8圈,前轮转动( )圈。
A.8 B.16 C.32 D.64
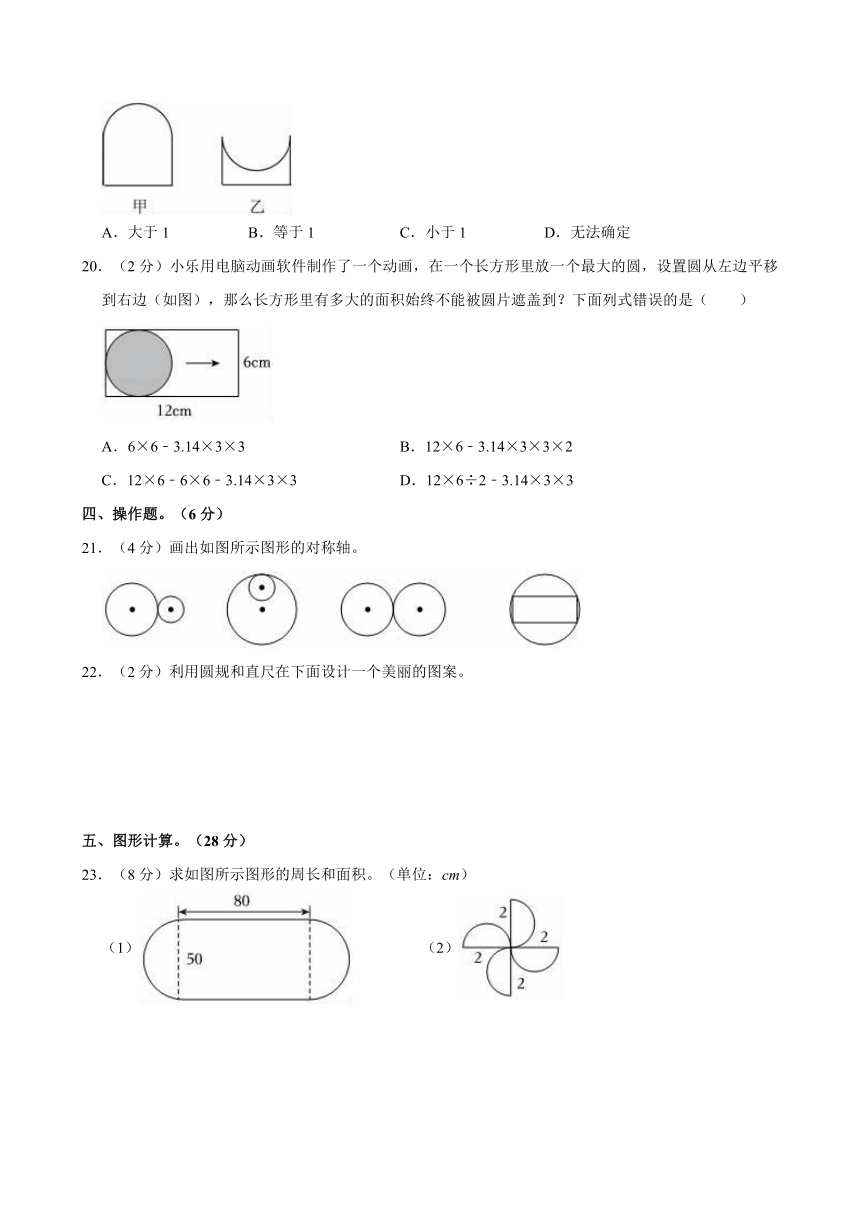
19.(2分)下面两个图形,甲的周长与乙的周长的比值是( )
A.大于1 B.等于1 C.小于1 D.无法确定
20.(2分)小乐用电脑动画软件制作了一个动画,在一个长方形里放一个最大的圆,设置圆从左边平移到右边(如图),那么长方形里有多大的面积始终不能被圆片遮盖到?下面列式错误的是( )
A.6×6﹣3.14×3×3 B.12×6﹣3.14×3×3×2
C.12×6﹣6×6﹣3.14×3×3 D.12×6÷2﹣3.14×3×3
四、操作题。(6分)
21.(4分)画出如图所示图形的对称轴。
22.(2分)利用圆规和直尺在下面设计一个美丽的图案。
五、图形计算。(28分)
23.(8分)求如图所示图形的周长和面积。(单位:cm)
(1) (2)
24.(20分)求各图形中阴影部分的面积。(单位:cm)
(1) (2)
(3) (4)
六、解决问题。(32分)
25.(5分)一挂钟的时针长10厘米,经过一昼夜时针的顶端走多少厘米?
26.(5分)校园里有一个周长为25.12m的圆形大花圃,在这个花圃中菊花的面积占,菊花的面积是多少平方米?
27.(5分)一辆轻便自行车的轮胎外直径约为60厘米,若平均每分钟转200周,小明家离学校约3768米,他从学校骑车回家大约需要多少分钟?
28.(5分)天宫一号与天宫二号目标飞行器是中国自主研制的载人空间实验平台,地球的半径大约是6400km,天宫一号在距地球表面340km高的圆形轨道上运转,天宫二号在距地球表面390km高的圆形轨道上运转,天宫二号比天宫一号的轨道长多少千米?
29.(6分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
30.(6分)把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形,量得这个长方形的周长比原来圆的周长增加了8cm。这个圆的面积是多少平方厘米?
七、附加题。(选做,另加10分)
31.(10分)如图,空地上有一栋房屋,房屋的墙角拴着一只羊,这座房屋长6m,宽4m。
(1)拴羊的绳长4m,羊在空地上的活动范围是多少平方米?
(2)如果拴羊的绳长换成6m,那么羊的活动范围增加了多少平方米?
参考答案
一、填空题。(第6题2分,其他每空1分,共19分)
1.解;因为圆是轴对称图形,且它的直径所在的直线就是其对称轴,而圆有无数条直径,所以圆就有无数条对称轴;
扇形只有沿从圆心到圆弧中点的连线对折,对折后的两部分才能完全重合,所以扇形只有一条对称轴.
答:圆有无数条对称轴,扇形有一条对称轴.
故答案为:无数、一.
2.解:6.28÷3.14=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
答:圆规两脚的距离应为2厘米,这个圆的面积是12.56平方厘米.
故答案为:2;12.56.
3.解:3.14×8=25.12(厘米)
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:圆的周长是25.12厘米,面积是50.24平方厘米。
故答案为:25.12,50.24。
4.解:设小圆的半径是r,则大圆的半径是2r,则:
(1)(2πr):[2×π×(2r)]
=2πr:4πr
=2÷4
=0.5
(2)π(2r)2:πr2
=4πr2:πr2
=4:1
答:小圆周长与大圆周长的比值是0.5,大圆面积与小圆面积的比是4:1.
故答案为:0.5,4:1.
5.解:3.14×(2÷2)2
=3.14×1
=3.14(平方分米)
3×2﹣3.14
=6﹣3.14
=2.86(平方分米)
答:这个圆的面积是3.14平方分米,剩下部分的面积是 2.86平方分米.
故答案为:3.14,2.86.
6.解:(1)3.14×22
=3.14×4
=12.56(平方厘米)
3.14×(2÷2)2×2
=3.14×2
=6.28(平方厘米)
6.28÷12.56=
答:两个小圆的面积之和是大圆面积的。
(2)2×3.14×2
=3.14×4
=12.56(厘米)
3.14×2×2
=3.14×4
=12.56(厘米)
答:两个小圆的周长之和等于大圆的周长。
故答案为:(1);(2)等于。
7.解:40÷2=20(米)
20+10=30(米)
3.14×(302﹣202)
=3.14×(900﹣400)
=3.14×500
=1570(平方米)
答:这个花坛扩建后的面积增加了1570平方米。
8.解:设半圆形的水池的直径是d米,
3.14×d÷2+d=10.28
2.57d=10.28
d=4,
半径为:4÷2=2(米);
面积为:3.14×22÷2
=3.14×4÷2
=6.28(平方米);
答:这个半圆形花坛的半径是2米,面积是6.28平方米;
故答案为:2米,6.28平方米.
9.解:3.14×4÷2=6.28(dm)
4÷2=2(dm)
(6.28+2)×2
=8.28×2
=16.56(dm)
6.28×2=12.56(dm2)
答:这个长方形的周长是16.56dm,面积是12.56dm2.
故答案为:16.56,12.56.
10.解:3.14×10+3.14×4
=31.4+12.56
=43.96(厘米)
3.14×(10÷2)2﹣3.14×(4÷2)2
=78.5﹣12.56
=65.94(平方厘米)
答:阴影部分的周长是43.96cm,面积是65.94cm2。
故答案为:43.96;65.94。
二、判断题。(对的画“√”,错的画“×”)(5分)
11.解:通过圆心,并且两端都在圆上的线段叫做直径,说法正确;
故答案为:√.
12.解:面积与周长的定义不同:圆的表面或围成的圆形表面的大小,叫做圆的面积;围成圆的一周的长度叫做这个圆的周长;
所采用的计量单位也不同:此题中,周长的单位是分米,面积的单位是平方分米,计量单位不能统一,所以没法比较它们的大小.
所以原题说法错误.
故答案为:×.
13.解:所有圆的周长和它的直径的比值都相等。原题说法正确。
故答案为:√。
14.解:当两个半圆的半径不相等时,不能拼成整圆。
故答案为:×。
15.解:如一个圆的面积是4平方厘米,而一个扇形的面积是8平方厘米.所以圆的面积比扇形的面积大.错误.
故答案为:×.
三、选择题。(将正确答案的序号填在括号里)(10分)
16.解:①圆的半径扩大到原来的2倍,那么周长都扩大到原来的2倍,面积扩大到原来的4倍,即原说法错误;
②半圆的周长包含半圆弧以及直径的长度,不等于圆周长的一半,即原说法错误;
③圆心角是90°的扇形的面积是所在圆面积的,而不是圆面积的,即原说法错误;
④正方形的面积是10cm2,即正方形边长的平方是10,边长的平方即半径的平方,所以圆面积=3.14×10=31.4(cm2),即原说法正确。
综上,只有④说法正确。
故选:A。
17.解:设圆的直径为4厘米,则正方形的边长也是4厘米,
圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米);
正方形的面积:
4×4=16(平方厘米);
16平方厘米>12.56平方厘米;
答:正方形的面积大于圆的面积.
如图:
故选:C.
18.解:设后轮转8圈前轮转x圈,再设前轮直径是1,则后轮直径是2,
1×3.14×x=2×3.14×8
3.14x=50.24
x=16
答:前轮滚动了16圈。
故选:B。
19.解:由分析可知:
甲的周长=乙的周长
甲的周长:乙的周长=1:1=1
甲的周长与乙的周长的比值是1,
故选:B.
20.解:6×6﹣3.14×(6÷2)2
=36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
或12×6﹣6×6﹣3.14×(6÷2)2
=72﹣36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
或12×6÷2﹣=72÷2﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
答:长方形里有7.74平方厘米的面积始终不能被圆片遮盖到。
所以列式错误的是12×6﹣3.14×3×3×2。
故选:B。
四、操作题。(6分)
21.解:
22.解:解答如下:
(画法不唯一)
五、图形计算。(28分)
23.解:(1)80×2+3.14×50
=160+157
=317(厘米)
3.14×(50÷2)2+80×50
=1962.5+4000
=5962.5(平方厘米)
答:这个图形的周长是317厘米,面积是5962.5平方厘米。
(2)4×2+3.14×2×2
=8+12.56
=20.56(厘米)
3.14×(2÷2)2×2
=3.14×2
=6.28(平方厘米)
答:这个图形的周长是20.56厘米,面积是6.28平方厘米。
24.解:(1)8÷2=4(厘米)
3.14×42﹣8×8÷2
=50.24﹣32
=18.24(平方厘米)
(2)4÷2=2(厘米)
4×6﹣3.14×22÷2
=24﹣6.28
=17.72(平方厘米)
(3)4×2=8(厘米)
4×8﹣3.14×42÷2
=32﹣25.12
=6.88(平方厘米)
(4)8÷2=4(厘米)
4+2=6(厘米)
3.14×(62﹣42)÷2
=3.14×20÷2
=31.4(平方厘米)
六、解决问题。(32分)
25.解:2×3.14×10×2,
=6.28×10×2,
=62.8×2,
=125.6(厘米);
答:经过一昼夜时针的顶端走125.6厘米.
26.解:3.14×(25.12÷3.14÷2)2×
=3.14×16×
=50.24×
=20.096(平方米)
答:菊花的面积是20.096平方米。
27.解:60厘米=0.6米
3.14×0.6×200
=3.14×120
=376.8(米)
3768÷376.8=10(分钟)
答:从学校骑车回家大约需要10分钟。
28.解:2×3.14×(6400+390)﹣2×3.14×(6400+340)
=2×3.14×6790﹣2×3.14×6740
=42641.2﹣42327.2
=314(千米)
答:天宫二号比天宫一号的轨道长314千米。
29.解:(9+6.7)×2
=15.7×2
=31.4(分米)
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
答:圆形铁皮的面积是78.5平方分米.
30.解:8÷2=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
七、附加题。(选做,另加10分)
31.解:(1)3.14×42×
=3.14×16×
=50.24×
=37.68(平方米)
答:羊在空地上的活动范围是37.68平方米。
(2)3.14×62×+3.14×(6﹣4)2×
=3.14×36×+3.14×4×
=84.78+3.14
=87.92(平方米)
87.92﹣37.68=50.24(平方米)
答:羊在空地上的活动范围增加50.24平方米。
一、填空题。(第6题2分,其他每空1分,共19分)
1.(2分)圆有 条对称轴,扇形有 条对称轴。
2.(2分)一个圆向右滚动后如图,要画一个同样的圆,那么圆规两脚的距离应为 厘米,这个圆的面积是 平方厘米。
3.(2分)如图所示,正方形的四个顶点均在圆上,已知正方形的对角线长8cm,圆的周长是 cm,面积是 cm2。
4.(2分)小圆的直径等于大圆的半径,小圆与大圆的周长的比值是 ,大圆与小圆面积的比是 。
5.(2分)在一个长3分米,宽为2分米的长方形里剪一个最大的圆,圆的面积是 平方分米,剩下部分的面积是 平方分米。
6.(2分)如图,小圆的直径是2厘米。
(1)两个小圆的面积之和是大圆面积的。
(2)两个小圆的周长之和 大圆的周长。(填“大于”“小于”或“等于”)
7.(1分)一个圆形花坛的直径是40m,扩建后,半径增加了10m,这个花坛扩建后的面积增加了 m2。
8.(2分)有一个半圆形的水池,量得它的周长是10.28米,这个水池的半径是 ,面积是 。
9.(2分)将一个直径是4dm的圆等分成若干份剪开,再拼成一个近似的长方形,这个长方形的周长是
dm,面积是 dm2。
10.(2分)如图,大半圆的直径是10cm,小半圆直径是4cm,阴影部分的周长是 cm,面积是 cm2。
二、判断题。(对的画“√”,错的画“×”)(5分)
11.(1分)通过圆心,并且两端都在圆上的线段叫做直径。 .
12.(1分)当圆的半径等于2分米时,这个圆的周长和面积相等。 .
13.(1分)所有圆的周长和它的直径的比值都相等。 .
14.(1分)两个半圆一定可以拼成一个整圆。 .
15.(1分)圆的面积比扇形的面积大。 .
三、选择题。(将正确答案的序号填在括号里)(10分)
16.(2分)下列说法中正确的有( )个。
①圆的半径扩大到原来的2倍,那么周长和面积都扩大到原来的2倍。
②半圆的周长是圆的周长的一半。
③圆心角是90°的扇形的面积是圆的面积的。
④如图,正方形的面积是10cm2,圆的面积是31.4cm2。
A.1 B.2 C.3 D.4
17.(2分)一个圆的直径与一个正方形的边长相等,它们的面积相比( )
A.相等 B.圆大 C.正方形大 D.不确定
18.(2分)一台拖拉机,后轮直径是前轮直径的2倍,后轮转动8圈,前轮转动( )圈。
A.8 B.16 C.32 D.64
19.(2分)下面两个图形,甲的周长与乙的周长的比值是( )
A.大于1 B.等于1 C.小于1 D.无法确定
20.(2分)小乐用电脑动画软件制作了一个动画,在一个长方形里放一个最大的圆,设置圆从左边平移到右边(如图),那么长方形里有多大的面积始终不能被圆片遮盖到?下面列式错误的是( )
A.6×6﹣3.14×3×3 B.12×6﹣3.14×3×3×2
C.12×6﹣6×6﹣3.14×3×3 D.12×6÷2﹣3.14×3×3
四、操作题。(6分)
21.(4分)画出如图所示图形的对称轴。
22.(2分)利用圆规和直尺在下面设计一个美丽的图案。
五、图形计算。(28分)
23.(8分)求如图所示图形的周长和面积。(单位:cm)
(1) (2)
24.(20分)求各图形中阴影部分的面积。(单位:cm)
(1) (2)
(3) (4)
六、解决问题。(32分)
25.(5分)一挂钟的时针长10厘米,经过一昼夜时针的顶端走多少厘米?
26.(5分)校园里有一个周长为25.12m的圆形大花圃,在这个花圃中菊花的面积占,菊花的面积是多少平方米?
27.(5分)一辆轻便自行车的轮胎外直径约为60厘米,若平均每分钟转200周,小明家离学校约3768米,他从学校骑车回家大约需要多少分钟?
28.(5分)天宫一号与天宫二号目标飞行器是中国自主研制的载人空间实验平台,地球的半径大约是6400km,天宫一号在距地球表面340km高的圆形轨道上运转,天宫二号在距地球表面390km高的圆形轨道上运转,天宫二号比天宫一号的轨道长多少千米?
29.(6分)一块圆形铁皮和一块长方形铁皮的周长相等,已知长方形的长为9dm,宽为6.7dm,圆形铁皮的面积是多少?
30.(6分)把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形,量得这个长方形的周长比原来圆的周长增加了8cm。这个圆的面积是多少平方厘米?
七、附加题。(选做,另加10分)
31.(10分)如图,空地上有一栋房屋,房屋的墙角拴着一只羊,这座房屋长6m,宽4m。
(1)拴羊的绳长4m,羊在空地上的活动范围是多少平方米?
(2)如果拴羊的绳长换成6m,那么羊的活动范围增加了多少平方米?
参考答案
一、填空题。(第6题2分,其他每空1分,共19分)
1.解;因为圆是轴对称图形,且它的直径所在的直线就是其对称轴,而圆有无数条直径,所以圆就有无数条对称轴;
扇形只有沿从圆心到圆弧中点的连线对折,对折后的两部分才能完全重合,所以扇形只有一条对称轴.
答:圆有无数条对称轴,扇形有一条对称轴.
故答案为:无数、一.
2.解:6.28÷3.14=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
答:圆规两脚的距离应为2厘米,这个圆的面积是12.56平方厘米.
故答案为:2;12.56.
3.解:3.14×8=25.12(厘米)
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:圆的周长是25.12厘米,面积是50.24平方厘米。
故答案为:25.12,50.24。
4.解:设小圆的半径是r,则大圆的半径是2r,则:
(1)(2πr):[2×π×(2r)]
=2πr:4πr
=2÷4
=0.5
(2)π(2r)2:πr2
=4πr2:πr2
=4:1
答:小圆周长与大圆周长的比值是0.5,大圆面积与小圆面积的比是4:1.
故答案为:0.5,4:1.
5.解:3.14×(2÷2)2
=3.14×1
=3.14(平方分米)
3×2﹣3.14
=6﹣3.14
=2.86(平方分米)
答:这个圆的面积是3.14平方分米,剩下部分的面积是 2.86平方分米.
故答案为:3.14,2.86.
6.解:(1)3.14×22
=3.14×4
=12.56(平方厘米)
3.14×(2÷2)2×2
=3.14×2
=6.28(平方厘米)
6.28÷12.56=
答:两个小圆的面积之和是大圆面积的。
(2)2×3.14×2
=3.14×4
=12.56(厘米)
3.14×2×2
=3.14×4
=12.56(厘米)
答:两个小圆的周长之和等于大圆的周长。
故答案为:(1);(2)等于。
7.解:40÷2=20(米)
20+10=30(米)
3.14×(302﹣202)
=3.14×(900﹣400)
=3.14×500
=1570(平方米)
答:这个花坛扩建后的面积增加了1570平方米。
8.解:设半圆形的水池的直径是d米,
3.14×d÷2+d=10.28
2.57d=10.28
d=4,
半径为:4÷2=2(米);
面积为:3.14×22÷2
=3.14×4÷2
=6.28(平方米);
答:这个半圆形花坛的半径是2米,面积是6.28平方米;
故答案为:2米,6.28平方米.
9.解:3.14×4÷2=6.28(dm)
4÷2=2(dm)
(6.28+2)×2
=8.28×2
=16.56(dm)
6.28×2=12.56(dm2)
答:这个长方形的周长是16.56dm,面积是12.56dm2.
故答案为:16.56,12.56.
10.解:3.14×10+3.14×4
=31.4+12.56
=43.96(厘米)
3.14×(10÷2)2﹣3.14×(4÷2)2
=78.5﹣12.56
=65.94(平方厘米)
答:阴影部分的周长是43.96cm,面积是65.94cm2。
故答案为:43.96;65.94。
二、判断题。(对的画“√”,错的画“×”)(5分)
11.解:通过圆心,并且两端都在圆上的线段叫做直径,说法正确;
故答案为:√.
12.解:面积与周长的定义不同:圆的表面或围成的圆形表面的大小,叫做圆的面积;围成圆的一周的长度叫做这个圆的周长;
所采用的计量单位也不同:此题中,周长的单位是分米,面积的单位是平方分米,计量单位不能统一,所以没法比较它们的大小.
所以原题说法错误.
故答案为:×.
13.解:所有圆的周长和它的直径的比值都相等。原题说法正确。
故答案为:√。
14.解:当两个半圆的半径不相等时,不能拼成整圆。
故答案为:×。
15.解:如一个圆的面积是4平方厘米,而一个扇形的面积是8平方厘米.所以圆的面积比扇形的面积大.错误.
故答案为:×.
三、选择题。(将正确答案的序号填在括号里)(10分)
16.解:①圆的半径扩大到原来的2倍,那么周长都扩大到原来的2倍,面积扩大到原来的4倍,即原说法错误;
②半圆的周长包含半圆弧以及直径的长度,不等于圆周长的一半,即原说法错误;
③圆心角是90°的扇形的面积是所在圆面积的,而不是圆面积的,即原说法错误;
④正方形的面积是10cm2,即正方形边长的平方是10,边长的平方即半径的平方,所以圆面积=3.14×10=31.4(cm2),即原说法正确。
综上,只有④说法正确。
故选:A。
17.解:设圆的直径为4厘米,则正方形的边长也是4厘米,
圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米);
正方形的面积:
4×4=16(平方厘米);
16平方厘米>12.56平方厘米;
答:正方形的面积大于圆的面积.
如图:
故选:C.
18.解:设后轮转8圈前轮转x圈,再设前轮直径是1,则后轮直径是2,
1×3.14×x=2×3.14×8
3.14x=50.24
x=16
答:前轮滚动了16圈。
故选:B。
19.解:由分析可知:
甲的周长=乙的周长
甲的周长:乙的周长=1:1=1
甲的周长与乙的周长的比值是1,
故选:B.
20.解:6×6﹣3.14×(6÷2)2
=36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
或12×6﹣6×6﹣3.14×(6÷2)2
=72﹣36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
或12×6÷2﹣=72÷2﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
答:长方形里有7.74平方厘米的面积始终不能被圆片遮盖到。
所以列式错误的是12×6﹣3.14×3×3×2。
故选:B。
四、操作题。(6分)
21.解:
22.解:解答如下:
(画法不唯一)
五、图形计算。(28分)
23.解:(1)80×2+3.14×50
=160+157
=317(厘米)
3.14×(50÷2)2+80×50
=1962.5+4000
=5962.5(平方厘米)
答:这个图形的周长是317厘米,面积是5962.5平方厘米。
(2)4×2+3.14×2×2
=8+12.56
=20.56(厘米)
3.14×(2÷2)2×2
=3.14×2
=6.28(平方厘米)
答:这个图形的周长是20.56厘米,面积是6.28平方厘米。
24.解:(1)8÷2=4(厘米)
3.14×42﹣8×8÷2
=50.24﹣32
=18.24(平方厘米)
(2)4÷2=2(厘米)
4×6﹣3.14×22÷2
=24﹣6.28
=17.72(平方厘米)
(3)4×2=8(厘米)
4×8﹣3.14×42÷2
=32﹣25.12
=6.88(平方厘米)
(4)8÷2=4(厘米)
4+2=6(厘米)
3.14×(62﹣42)÷2
=3.14×20÷2
=31.4(平方厘米)
六、解决问题。(32分)
25.解:2×3.14×10×2,
=6.28×10×2,
=62.8×2,
=125.6(厘米);
答:经过一昼夜时针的顶端走125.6厘米.
26.解:3.14×(25.12÷3.14÷2)2×
=3.14×16×
=50.24×
=20.096(平方米)
答:菊花的面积是20.096平方米。
27.解:60厘米=0.6米
3.14×0.6×200
=3.14×120
=376.8(米)
3768÷376.8=10(分钟)
答:从学校骑车回家大约需要10分钟。
28.解:2×3.14×(6400+390)﹣2×3.14×(6400+340)
=2×3.14×6790﹣2×3.14×6740
=42641.2﹣42327.2
=314(千米)
答:天宫二号比天宫一号的轨道长314千米。
29.解:(9+6.7)×2
=15.7×2
=31.4(分米)
3.14×(31.4÷3.14÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
答:圆形铁皮的面积是78.5平方分米.
30.解:8÷2=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
七、附加题。(选做,另加10分)
31.解:(1)3.14×42×
=3.14×16×
=50.24×
=37.68(平方米)
答:羊在空地上的活动范围是37.68平方米。
(2)3.14×62×+3.14×(6﹣4)2×
=3.14×36×+3.14×4×
=84.78+3.14
=87.92(平方米)
87.92﹣37.68=50.24(平方米)
答:羊在空地上的活动范围增加50.24平方米。
同课章节目录
