4.1.1 n次方根与分数指数幂 课件(共47张PPT)-高一数学必修第一册同步高效课堂(人教A版2019)
文档属性
| 名称 | 4.1.1 n次方根与分数指数幂 课件(共47张PPT)-高一数学必修第一册同步高效课堂(人教A版2019) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-25 10:06:35 | ||
图片预览











文档简介
(共47张PPT)
第 4 章
4.1.1 n次方根与分数指数幂
人教A版2019必修第一册
4.1.1 n次方根与分数指数幂
学习目标
1.理解n次方根、根式的概念.
2.能正确运用根式的运算性质化简、求值.(重点)
3.会对分式和分数指数幂进行转化.(重点)
4.掌握并运用有理数指数幂的运算性质化简、求值.(难点)
目录
CATALOG
01.分数指数幂
03.题型强化训练
02.有理数指数幂的运算性质
04.小结及随堂练习
01
分数指数幂
4.1.1 n次方根与分数指数幂
导入新知
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现.这里的巨型城址,面积近630万平方米,包括古城、水坝和多处高等级建筑.考古学家利用遗址中遗存物碳14的残留测定,古城存在时期为公元前3300年——前2300年.你知道考古学家在测定遗址年代时用了什么数学知识吗?
实际上,考古学家所用的数学知识就是本章即将要学的指数函数.为了研究指数函数,我们需要把指数的范围拓展到全体实数.
导入新知
为了研究指数函数,我们需要把指数的范围拓展到全体实数。初中已经学过整数指数幂.
幂
指数
底数
读作“a的n次方”或“a的n次幂”
求n个相同因数的积的运算,叫做乘方,
乘方的结果叫做幂.
学习新知
初中已经学习过整数指数幂.在学习幂函数时,我们把正方形的边长关于面积的函数记作.像这样以分数为指数的幂,其意义是什么呢?下面从已知的平方根、立方根的意义展开研究.
叫做的平方根.例如,就是4的平方根.
叫做的立方根.例如,就是8的立方根.
叫做16的四次方根.例如,2叫做32的五次方根.
学习新知
一般地,如果,那么叫做的次方根,其中,且
当是奇数时,正数的次方根是一个正数,负数的次方根是一个负数.这时,的次方根用符号表示.
例如,,.
当是偶数时,正数的次方根有两个,这两个数互为相反数.这时,正数的正的次方根用符号表示表示,负的次方根用符号表示表示.正的次方根与负的次方根可以合并写成.
例如,,,
学习新知
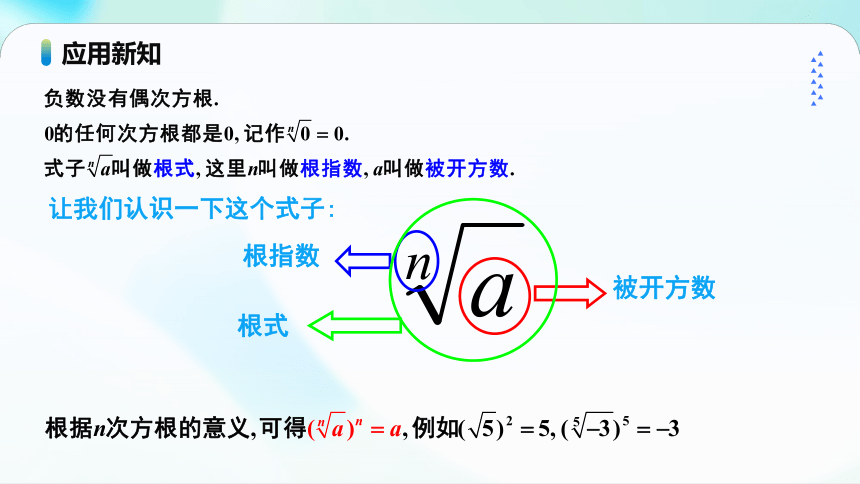
任何数连续偶数次相乘后,一定会得正数或0,因此,负数没有偶次方根.
0的任何次方根都是0,记作
式子叫做根式,这里叫做根指数,叫做被开方数.
根据次方根的意义,可得:
例如,
应用新知
让我们认识一下这个式子:
根指数
被开方数
根式
学习新知
例如,
应用新知
应用新知
学习新知
这就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除吋,根式可以表示为分数指数幂的形式.
当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
学习新知
学习新知
数学中,引进一个新的概念或法则时,总希望它与已有的概念或法则相容.
这里,略去了规定合理性的说明.
学习新知
与0的整数指数幂的意义相仿,我们规定,
0的正分数指数幂等于0, 0的负分数指数幂没有意义.
总结新知
根式
分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;
0的负分数指数幂无意义.
三、分数指数幂
02
有理数指数幂的
运算性质
4.1.1 n次方根与分数指数幂
应用新知
应用新知
应用新知
根式化简与求值的思路及注意点:
(1)思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质
进行化简.
(2)注意点:
①正确区分“ ”与“ ”两式;(注意分析 是否有意义)
②运算时注意变式、整体代换,以及平方差、立方差和完全平方公式、完全立方公式的运用,必要时要进行讨论.
总结新知
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;0的负分数指数幂无意义.
(4)分数指数幂不可随意约分;
(5)有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
应用新知
应用新知
学习新知
学习新知
应用新知
利用指数幂的运算性质化简求值的方法:
(1)进行指数幂的运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序;
(2)在明确根指数的奇偶(或具体次数)时,若能明确被开方数的符号,则可以对根式进行化简运算;
(3)对于含有字母的化简求值的结果,一般用分数指数幂的形式表示.
总结新知
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式:
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
总结新知
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
总结新知
整数指数幂的运算性质:
整数指数幂:
指数运算
03
题型强化训练
4.1.1 n次方根与分数指数幂
能力提升
题型一 根式的化简与求值
【感悟提升】根式化简与求值的注意点
(1)分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简与求值.
(2)在化简含有字母的根式时要注意字母的取值范围.
(3)运算时注意变式、整体代换,以及平方差、立方差、完全平方、完全立方公式的运用.
(4)注意分类讨论思想的应用.
能力提升
题型二:根式与分数指数幂的互化
能力提升
题型三:有理数指数幂的运算
【感悟提升】 指数幂运算的解题通法
(1)有括号的先算括号里的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数,先化成假分数.
(4)若是根式,应化为分数指数幂,并尽可能用幂的形式表示,运用指数幂的运算性质来解答.
(5)运算结果不能同时含有根式和分数指数幂,也不能既有分母又含有负指数幂,形式力求统一.
能力提升
题型三:有理数指数幂的运算
方法技巧:
条件求值是代数式求值中的常见题型,一般要结合已知条件先化简再求值,另外要特别注意条件的应用,如条件中的隐含条件,整体代入等,可以简化解题过程.
04
小结及随堂练习
4.1.1 n次方根与分数指数幂
课堂小结1
1.知识清单:
(1)n次方根的概念、表示及性质.
(2)根式的性质.
(3)根式与分数指数幂的互化.
2.常见误区:
(1)根式中根指数要求n>1且n∈N*.
(2)对于 ,当n为偶数时,a≥0.
课堂小结2
课堂小结
(1)方根个数:正数的偶次方根有两个且互为相反数,任意实数的奇次方根只有一个.
(2)符号:根式 的符号由根指数n的奇偶性及被开方数a的符号共同确定.
①当n为偶数,且a≥0时, 为非负实数;
②当n为奇数时, 的符号与a的符号一致.
根式与分数指数幂的互化
(1)根指数化为分数指数的分母,被开方数(式)的指数化为分数指数的分子.
(2)在具体计算时,如果底数相同,通常会把根式转化成分数指数幂的形式,然后利用有理数指数幂的运算性质解题.
课堂小结1
整数指数幂 分数指数幂
正数
负数 0
无理数指数幂
实数指数幂ax(a>0)
实数指数幂的运算性质(a>0 ; r,s∈R):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
类比推广:实数指数幂
作业
1.P107 练习1.2.3题;
2.P109 练习1题&习题第1、2、4、5题
4.1.1 n次方根与分数指数幂
练习(第107页)
练习(第107页)
练习(第107页)
练习(第107页)
人教A版2019必修第一册
THANKS
感谢您的聆听
第 4 章
4.1.1 n次方根与分数指数幂
人教A版2019必修第一册
4.1.1 n次方根与分数指数幂
学习目标
1.理解n次方根、根式的概念.
2.能正确运用根式的运算性质化简、求值.(重点)
3.会对分式和分数指数幂进行转化.(重点)
4.掌握并运用有理数指数幂的运算性质化简、求值.(难点)
目录
CATALOG
01.分数指数幂
03.题型强化训练
02.有理数指数幂的运算性质
04.小结及随堂练习
01
分数指数幂
4.1.1 n次方根与分数指数幂
导入新知
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现.这里的巨型城址,面积近630万平方米,包括古城、水坝和多处高等级建筑.考古学家利用遗址中遗存物碳14的残留测定,古城存在时期为公元前3300年——前2300年.你知道考古学家在测定遗址年代时用了什么数学知识吗?
实际上,考古学家所用的数学知识就是本章即将要学的指数函数.为了研究指数函数,我们需要把指数的范围拓展到全体实数.
导入新知
为了研究指数函数,我们需要把指数的范围拓展到全体实数。初中已经学过整数指数幂.
幂
指数
底数
读作“a的n次方”或“a的n次幂”
求n个相同因数的积的运算,叫做乘方,
乘方的结果叫做幂.
学习新知
初中已经学习过整数指数幂.在学习幂函数时,我们把正方形的边长关于面积的函数记作.像这样以分数为指数的幂,其意义是什么呢?下面从已知的平方根、立方根的意义展开研究.
叫做的平方根.例如,就是4的平方根.
叫做的立方根.例如,就是8的立方根.
叫做16的四次方根.例如,2叫做32的五次方根.
学习新知
一般地,如果,那么叫做的次方根,其中,且
当是奇数时,正数的次方根是一个正数,负数的次方根是一个负数.这时,的次方根用符号表示.
例如,,.
当是偶数时,正数的次方根有两个,这两个数互为相反数.这时,正数的正的次方根用符号表示表示,负的次方根用符号表示表示.正的次方根与负的次方根可以合并写成.
例如,,,
学习新知
任何数连续偶数次相乘后,一定会得正数或0,因此,负数没有偶次方根.
0的任何次方根都是0,记作
式子叫做根式,这里叫做根指数,叫做被开方数.
根据次方根的意义,可得:
例如,
应用新知
让我们认识一下这个式子:
根指数
被开方数
根式
学习新知
例如,
应用新知
应用新知
学习新知
这就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除吋,根式可以表示为分数指数幂的形式.
当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
学习新知
学习新知
数学中,引进一个新的概念或法则时,总希望它与已有的概念或法则相容.
这里,略去了规定合理性的说明.
学习新知
与0的整数指数幂的意义相仿,我们规定,
0的正分数指数幂等于0, 0的负分数指数幂没有意义.
总结新知
根式
分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;
0的负分数指数幂无意义.
三、分数指数幂
02
有理数指数幂的
运算性质
4.1.1 n次方根与分数指数幂
应用新知
应用新知
应用新知
根式化简与求值的思路及注意点:
(1)思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质
进行化简.
(2)注意点:
①正确区分“ ”与“ ”两式;(注意分析 是否有意义)
②运算时注意变式、整体代换,以及平方差、立方差和完全平方公式、完全立方公式的运用,必要时要进行讨论.
总结新知
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;0的负分数指数幂无意义.
(4)分数指数幂不可随意约分;
(5)有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
应用新知
应用新知
学习新知
学习新知
应用新知
利用指数幂的运算性质化简求值的方法:
(1)进行指数幂的运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序;
(2)在明确根指数的奇偶(或具体次数)时,若能明确被开方数的符号,则可以对根式进行化简运算;
(3)对于含有字母的化简求值的结果,一般用分数指数幂的形式表示.
总结新知
(n为奇数)
(当n是偶数,且a>0)
0的任何次方根都是0,记作 .
根式:
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
n次方根定义:
一般地,如果xn=a,则x叫做a的n次方根,其中n>1,且n∈N*.
总结新知
正数的正分数指数幂:
正数的负分数指数幂:
规定:0的正分数指数幂等于0,0的负分数指数幂没意义.
指数运算性质:
总结新知
整数指数幂的运算性质:
整数指数幂:
指数运算
03
题型强化训练
4.1.1 n次方根与分数指数幂
能力提升
题型一 根式的化简与求值
【感悟提升】根式化简与求值的注意点
(1)分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简与求值.
(2)在化简含有字母的根式时要注意字母的取值范围.
(3)运算时注意变式、整体代换,以及平方差、立方差、完全平方、完全立方公式的运用.
(4)注意分类讨论思想的应用.
能力提升
题型二:根式与分数指数幂的互化
能力提升
题型三:有理数指数幂的运算
【感悟提升】 指数幂运算的解题通法
(1)有括号的先算括号里的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数,先化成假分数.
(4)若是根式,应化为分数指数幂,并尽可能用幂的形式表示,运用指数幂的运算性质来解答.
(5)运算结果不能同时含有根式和分数指数幂,也不能既有分母又含有负指数幂,形式力求统一.
能力提升
题型三:有理数指数幂的运算
方法技巧:
条件求值是代数式求值中的常见题型,一般要结合已知条件先化简再求值,另外要特别注意条件的应用,如条件中的隐含条件,整体代入等,可以简化解题过程.
04
小结及随堂练习
4.1.1 n次方根与分数指数幂
课堂小结1
1.知识清单:
(1)n次方根的概念、表示及性质.
(2)根式的性质.
(3)根式与分数指数幂的互化.
2.常见误区:
(1)根式中根指数要求n>1且n∈N*.
(2)对于 ,当n为偶数时,a≥0.
课堂小结2
课堂小结
(1)方根个数:正数的偶次方根有两个且互为相反数,任意实数的奇次方根只有一个.
(2)符号:根式 的符号由根指数n的奇偶性及被开方数a的符号共同确定.
①当n为偶数,且a≥0时, 为非负实数;
②当n为奇数时, 的符号与a的符号一致.
根式与分数指数幂的互化
(1)根指数化为分数指数的分母,被开方数(式)的指数化为分数指数的分子.
(2)在具体计算时,如果底数相同,通常会把根式转化成分数指数幂的形式,然后利用有理数指数幂的运算性质解题.
课堂小结1
整数指数幂 分数指数幂
正数
负数 0
无理数指数幂
实数指数幂ax(a>0)
实数指数幂的运算性质(a>0 ; r,s∈R):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
类比推广:实数指数幂
作业
1.P107 练习1.2.3题;
2.P109 练习1题&习题第1、2、4、5题
4.1.1 n次方根与分数指数幂
练习(第107页)
练习(第107页)
练习(第107页)
练习(第107页)
人教A版2019必修第一册
THANKS
感谢您的聆听
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
