4.1.2 无理数指数幂及其运算性质 课件(共44张PPT)-高一数学必修第一册同步高效课堂(人教A版2019)
文档属性
| 名称 | 4.1.2 无理数指数幂及其运算性质 课件(共44张PPT)-高一数学必修第一册同步高效课堂(人教A版2019) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-25 10:07:03 | ||
图片预览









文档简介
(共44张PPT)
第 4 章
4.1.2 无理数指数幂及其运算性质
人教A版2019必修第一册
无理数指数幂及其运算性质
学习目标
1.能结合教材探究了解无理数指数幂.
2.结合有理数指数幂的运算性质掌握实数指数幂的运算性质.
目录
CATALOG
01.无理数指数幂
03.题型强化训练
02.实数指数幂的运算性质
04.小结及随堂练习
01
无理数指数幂
4.1.2 无理数指数幂及其运算性质
导入新知
公元前5世纪,古希腊有一个数学学派名叫毕达哥拉斯学派,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线长度是多少呢?他发现这一长度既不能用整数,也不能用分数来表示,希帕索斯的发现导致了数学史上第一个无理数内的诞生.
希帕索斯
思考
根据初中所学知识,思考一下边长为1的正方形的对角线长是如何计算出来的呢?
提示
根据勾股定理可以计算出正方形的对角线长为上面我们将中指数的取值范围从整数拓展到了有理数.
那么,当指数是无理数时意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质呢?
导入新知
学习新知
在初中的学习中,我么通过有理数认识了一些无理数.类似地,也可以通过有理数指数幂来认识无理数指数幂.
学习新知
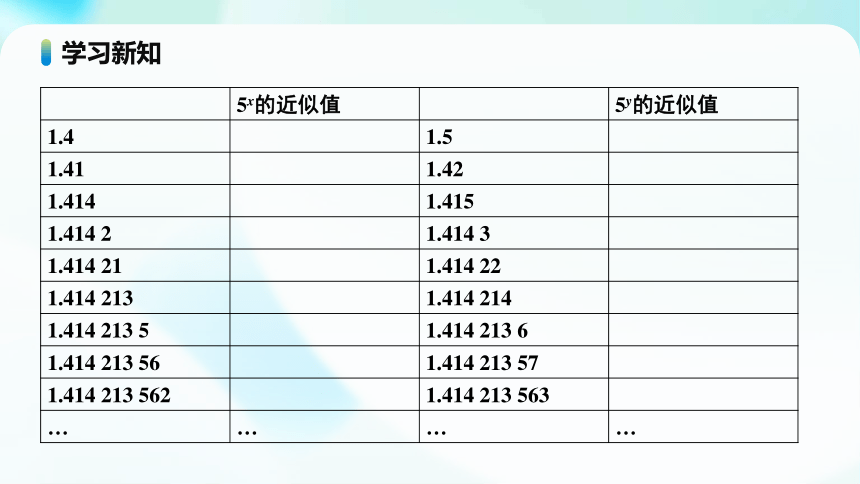
5x的近似值 5y的近似值
1.4 1.5
1.41 1.42
1.414 1.415
1.414 2 1.414 3
1.414 21 1.414 22
1.414 213 1.414 214
1.414 213 5 1.414 213 6
1.414 213 56 1.414 213 57
1.414 213 562 1.414 213 563
… … … …
学习新知
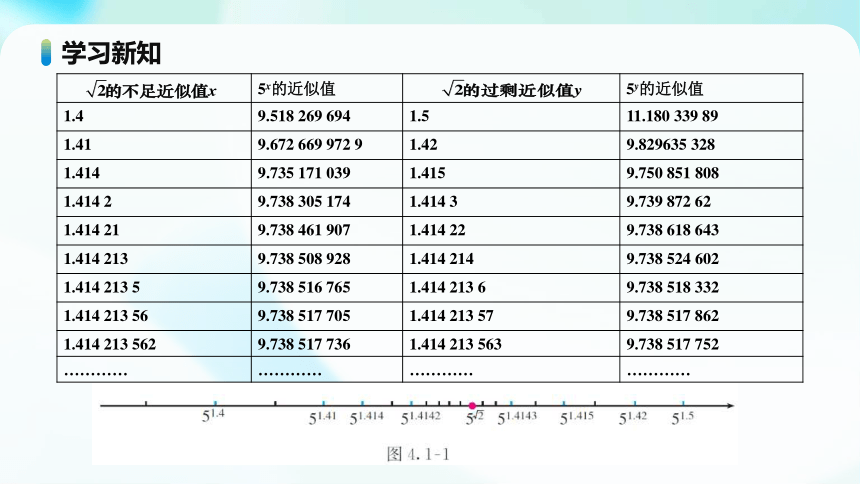
5x的近似值 5y的近似值
1.4 9.518 269 694 1.5 11.180 339 89
1.41 9.672 669 972 9 1.42 9.829635 328
1.414 9.735 171 039 1.415 9.750 851 808
1.414 2 9.738 305 174 1.414 3 9.739 872 62
1.414 21 9.738 461 907 1.414 22 9.738 618 643
1.414 213 9.738 508 928 1.414 214 9.738 524 602
1.414 213 5 9.738 516 765 1.414 213 6 9.738 518 332
1.414 213 56 9.738 517 705 1.414 213 57 9.738 517 862
1.414 213 562 9.738 517 736 1.414 213 563 9.738 517 752
………… ………… ………… …………
学习新知
02
实数指数幂
的运算性质
4.1.2 无理数指数幂及其运算性质
学习新知
学习新知
反思感悟 关于无理数指数幂的运算
(1)无理数指数幂的运算性质与有理数指数幂的运算性质相同.
(2)若式子中含有根式,一般把底数中的根式化为指数式,指数中的根式可以保留直接运算.
学习新知
应用新知
反思感悟 指数运算在实际问题中的应用
在成倍数递增(递减)、固定增长率等问题中,常常用到指数运算,用来计算增减的次数、增减前后的数量等.
应用新知
总结新知
无理数指数幂
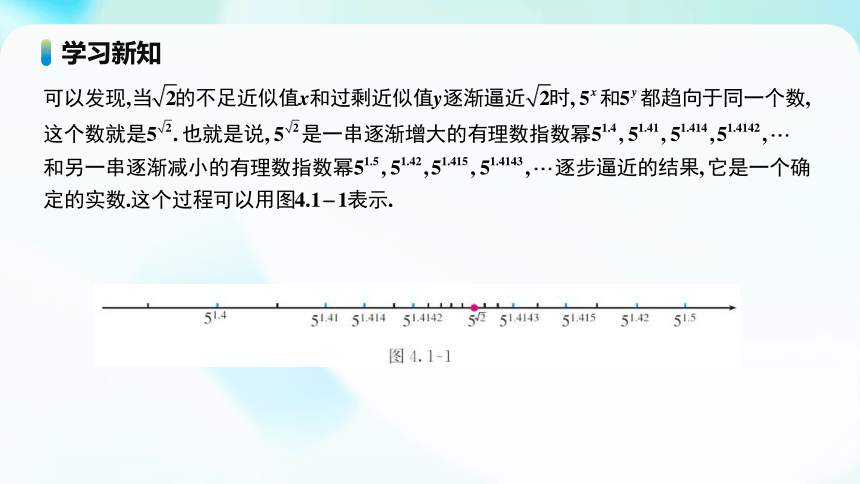
(1)对于无理数指数幂,我们只需要了解两点:①它是一个确定的实数;②它是有理数指数幂无限逼近的结果.
(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.
实数指数幂的运算性质
(1)aras=_____(a>0,r,s∈R).
(2)(ar)s=____ (a>0,r,s∈R).
(3)(ab)r=____ (a>0,b>0,r∈R).
[拓展] =ar-s(a>0,r,s∈R).
[提醒] 实数指数幂中一定要有a>0.
ar+s
ars
arbr
03
题型强化训练
4.1.2 无理数指数幂及其运算性质
能力提升
题型一 无理数指数幂的运算
【感悟提升】 关于无理数指数幂的运算
(1)无理数指数幂的运算性质与有理数指数幂的运算性质相同.
(2)若式子中含有根式,一般把底数中的根式化为指数式,指数中的根式可以保留直接运算.
能力提升
题型二 实际问题中的指数运算
【感悟提升】 指数运算在实际问题中的应用
在成倍数递增(递减)、固定增长率(下降率)等问题中,常用到指数运算,用来计算增减的次数、增减前后的数量等.
能力提升
题型三 指数幂运算中的条件求值
能力提升
题型三 指数幂运算中的条件求值
04
小结及随堂练习
4.1.2 无理数指数幂及其运算性质
课堂小结
1.知识清单:
(1)无理数指数幂的运算.
(2)实际问题中的指数运算.
(3)实数指数幂的综合运用.
2.方法归纳:整体代换法.
3.常见误区:在运用分数指数幂的运算性质化简时,其结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
课堂小结
作业
1.完成教材第109页练习第1题,第2题.
2.完成教材第110页习题4. 1第7题,第8题.
4.1.2 无理数指数幂及其运算性质
练习(第109页)
练习(第109页)
习题4.1(第109页)
习题4.1(第109页)
D
习题4.1(第109页)
A
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
6.如果在某种细菌培养过程中,细菌每10 min分裂1次(1个分裂成2个),那么经过1h,1个这种细菌可以分裂成 个.
∵细菌每10 min分裂1次,1h共分裂6次,
∴1个细菌分裂成 26=64个
64
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
人教A版2019必修第一册
THANKS
感谢您的聆听
第 4 章
4.1.2 无理数指数幂及其运算性质
人教A版2019必修第一册
无理数指数幂及其运算性质
学习目标
1.能结合教材探究了解无理数指数幂.
2.结合有理数指数幂的运算性质掌握实数指数幂的运算性质.
目录
CATALOG
01.无理数指数幂
03.题型强化训练
02.实数指数幂的运算性质
04.小结及随堂练习
01
无理数指数幂
4.1.2 无理数指数幂及其运算性质
导入新知
公元前5世纪,古希腊有一个数学学派名叫毕达哥拉斯学派,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线长度是多少呢?他发现这一长度既不能用整数,也不能用分数来表示,希帕索斯的发现导致了数学史上第一个无理数内的诞生.
希帕索斯
思考
根据初中所学知识,思考一下边长为1的正方形的对角线长是如何计算出来的呢?
提示
根据勾股定理可以计算出正方形的对角线长为上面我们将中指数的取值范围从整数拓展到了有理数.
那么,当指数是无理数时意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质呢?
导入新知
学习新知
在初中的学习中,我么通过有理数认识了一些无理数.类似地,也可以通过有理数指数幂来认识无理数指数幂.
学习新知
5x的近似值 5y的近似值
1.4 1.5
1.41 1.42
1.414 1.415
1.414 2 1.414 3
1.414 21 1.414 22
1.414 213 1.414 214
1.414 213 5 1.414 213 6
1.414 213 56 1.414 213 57
1.414 213 562 1.414 213 563
… … … …
学习新知
5x的近似值 5y的近似值
1.4 9.518 269 694 1.5 11.180 339 89
1.41 9.672 669 972 9 1.42 9.829635 328
1.414 9.735 171 039 1.415 9.750 851 808
1.414 2 9.738 305 174 1.414 3 9.739 872 62
1.414 21 9.738 461 907 1.414 22 9.738 618 643
1.414 213 9.738 508 928 1.414 214 9.738 524 602
1.414 213 5 9.738 516 765 1.414 213 6 9.738 518 332
1.414 213 56 9.738 517 705 1.414 213 57 9.738 517 862
1.414 213 562 9.738 517 736 1.414 213 563 9.738 517 752
………… ………… ………… …………
学习新知
02
实数指数幂
的运算性质
4.1.2 无理数指数幂及其运算性质
学习新知
学习新知
反思感悟 关于无理数指数幂的运算
(1)无理数指数幂的运算性质与有理数指数幂的运算性质相同.
(2)若式子中含有根式,一般把底数中的根式化为指数式,指数中的根式可以保留直接运算.
学习新知
应用新知
反思感悟 指数运算在实际问题中的应用
在成倍数递增(递减)、固定增长率等问题中,常常用到指数运算,用来计算增减的次数、增减前后的数量等.
应用新知
总结新知
无理数指数幂
(1)对于无理数指数幂,我们只需要了解两点:①它是一个确定的实数;②它是有理数指数幂无限逼近的结果.
(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.
实数指数幂的运算性质
(1)aras=_____(a>0,r,s∈R).
(2)(ar)s=____ (a>0,r,s∈R).
(3)(ab)r=____ (a>0,b>0,r∈R).
[拓展] =ar-s(a>0,r,s∈R).
[提醒] 实数指数幂中一定要有a>0.
ar+s
ars
arbr
03
题型强化训练
4.1.2 无理数指数幂及其运算性质
能力提升
题型一 无理数指数幂的运算
【感悟提升】 关于无理数指数幂的运算
(1)无理数指数幂的运算性质与有理数指数幂的运算性质相同.
(2)若式子中含有根式,一般把底数中的根式化为指数式,指数中的根式可以保留直接运算.
能力提升
题型二 实际问题中的指数运算
【感悟提升】 指数运算在实际问题中的应用
在成倍数递增(递减)、固定增长率(下降率)等问题中,常用到指数运算,用来计算增减的次数、增减前后的数量等.
能力提升
题型三 指数幂运算中的条件求值
能力提升
题型三 指数幂运算中的条件求值
04
小结及随堂练习
4.1.2 无理数指数幂及其运算性质
课堂小结
1.知识清单:
(1)无理数指数幂的运算.
(2)实际问题中的指数运算.
(3)实数指数幂的综合运用.
2.方法归纳:整体代换法.
3.常见误区:在运用分数指数幂的运算性质化简时,其结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
课堂小结
作业
1.完成教材第109页练习第1题,第2题.
2.完成教材第110页习题4. 1第7题,第8题.
4.1.2 无理数指数幂及其运算性质
练习(第109页)
练习(第109页)
习题4.1(第109页)
习题4.1(第109页)
D
习题4.1(第109页)
A
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
6.如果在某种细菌培养过程中,细菌每10 min分裂1次(1个分裂成2个),那么经过1h,1个这种细菌可以分裂成 个.
∵细菌每10 min分裂1次,1h共分裂6次,
∴1个细菌分裂成 26=64个
64
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
习题4.1(第109页)
人教A版2019必修第一册
THANKS
感谢您的聆听
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
