11.1 平方根(同步课件)-八年级数学上册同步精品课堂(北京版)
文档属性
| 名称 | 11.1 平方根(同步课件)-八年级数学上册同步精品课堂(北京版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
11.1 平方根
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1、理解算术平方根的概念,会用根号表示正数的算术平方根.
2、理解算术平方根的非负性.
3、通过平方运算求某些非负数的算术平方根.
4、掌握平方根的意义及性质.
5、理解平方根与算术平方根的联系与区别.
导入新课
自由下落物体的高度 (米)与下落时间 (秒)的关系为h=4.9t2 .有
一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:当h=10时 ,得19.6=4.9t2 ,
所以 t2=4
那t应为何值呢?
讲授新课
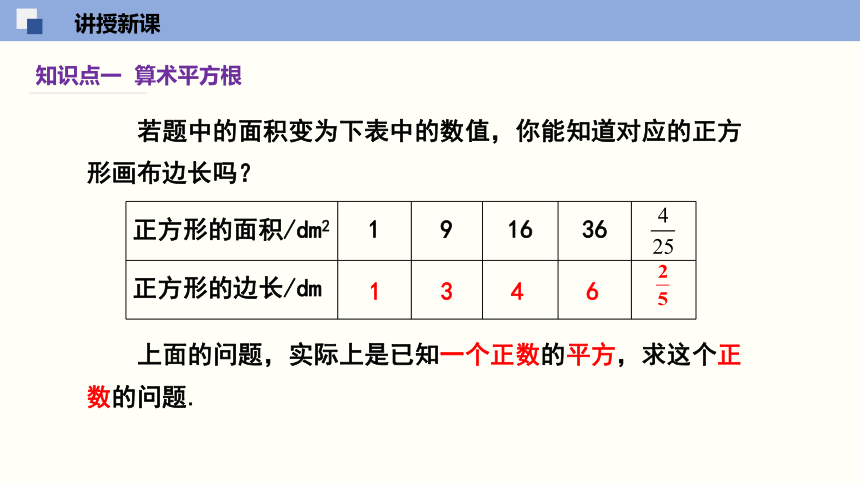
知识点一 算术平方根
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
若题中的面积变为下表中的数值,你能知道对应的正方形画布边长吗?
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
讲授新课
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根. a的算术平方根记为 ,读作“根号a”,a叫做被开方数.
0的算术平方根是0.
记作:
规定:
讲授新课
试一试:1.你能根据等式 122=144,说出144的的算术平方根是多少吗?并用等式表示出来.
144的算术平方根是12,即=12.
x时,就是2的算术平方根,即
y时,y就是3的算术平方根,即
w时,w就是5的算术平方根,即
z时,z就是4的算术平方根,即
2.试求出上面问题中的x、y、z、w的值.
非平方数的算术平方根只能用根号表示.
讲授新课
典例精析
解: (1)因为302=900, 所以900的算术平方根是30,即=30;
【例1】求下列各数的算术平方根:
(1) 900; (2) 1; (3) ; (4) 14.
(3)因为,所以的算术平方根是,即;
(2)因为12=1, 所以1的算术平方根是1,即=1;
(4)14的算术平方根是.
讲授新课
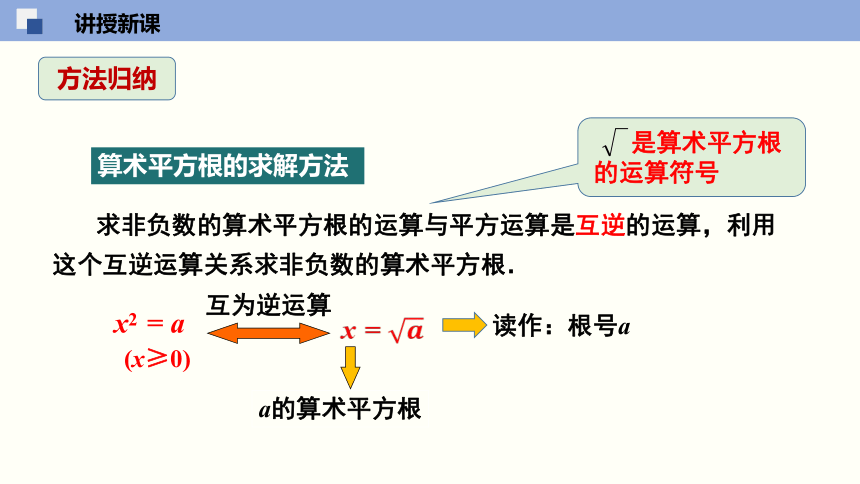
方法归纳
a的算术平方根
互为逆运算
求非负数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
是算术平方根的运算符号
x =
x2 = a
(x≥0)
算术平方根的求解方法
读作:根号a
讲授新课
练一练
1、计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
讲授新课
2.若一个数的算术平方根是 ,那么这个数是 ;
3. 的算术平方根是 ;
4. 的算术平方根是 ;
5.若 ,则 .
7
16
讲授新课
知识点二 算术平方根的性质
想一想:(1)负数有算术平方根吗?
只有非负数(正数和0)有算术平方根,负数没有算术平方根(即当a<0时,无意义).
(2)一个非负数的算术平方根可能是负数吗?
不可能,非负数的算术平方根是非负数.
讲授新课
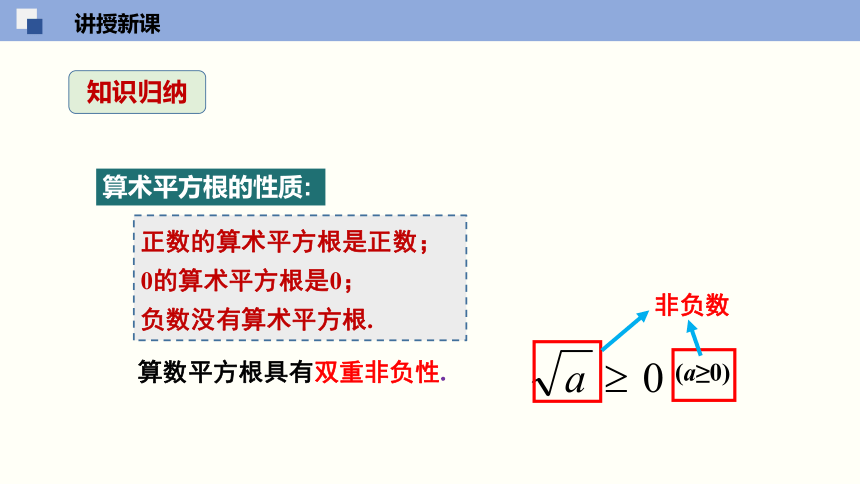
算数平方根具有双重非负性.
(a≥0)
非负数
算术平方根的性质:
正数的算术平方根是正数;
0的算术平方根是0;
负数没有算术平方根.
知识归纳
讲授新课
典例精析
解: 因为|m-1| ≥0,≥0,又|m-1| +=0,
所以 |m-1| =0,=0,
所以m=1,n=-3,
所以m+n=1+(-3)=-2.
【例2】若|m-1| + =0,求m+n的值.
归纳:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
讲授新课
练一练
1.已知: 求X-3Y+4Z的值.
解:由题意得:
解得
讲授新课
知识点三 算术平方根的实际应用
解:将s=19.6代入公式
s=4.9t2,
得 t2 =4 ,
所以正数 t2 =(秒).
即铁球到达地面需要2秒.
做一做:自由下落物体下落的距离s(米)与下落时间t(秒)的关系为s=4.9.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
讲授新课
典例精析
【例3】如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为5.5米,地面固定点C到帐篷支撑竿底部B的距离是4.5米,则帐篷支撑竿的高是多少米?
所以帐篷支撑竿的高是米.
解:由题意得AC=5.5米,BC=4.5米,∠ABC=90°.
在Rt△ABC中,由勾股定理得
==(米)
讲授新课
练一练
h
d
1、“欲穷千里目,更上一层楼”,说的是登得高看得远.如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 ,其中R是地球半径,约等于6400 km.小丽站在海边的一块岩石上,眼睛离海平面的高度h为20 m,她观测到远处一艘船刚露出海平面,求此时d的值.
解:
由R=6400 km,h=0.02 km,得
讲授新课
知识点四 平方根的概念及其性质
(2)平方等于正数的数都有几个,它们有什么关系?
平方等于正数的数有2个,它们互为相反数.
想一想:(1)平方等于的数有几个 平方等于 0.64 的数呢
平方等于的数有2个,即和;
平方等于 0.64 的数也有2个,即±0.8.
讲授新课
知识归纳
一般地,如果一个数x的平方等于a,即x2= a,那么这个数x叫做a的平方根(也叫二次方根).
例如:(±4)2=16,则4和-4都是16的平方根;
即16的平方根是4和-4;其中,4还是16的算术平方根.
平方根的概念
讲授新课
议一议:(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?
(3)因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
平方根的性质:一个正数有两个平方根(互为相反数);0只有一个平方根,它是0本身;负数没有平方根.
2个
1个
平方根如何表示呢?
讲授新课
知识归纳
正数a有两个平方根,一个是a的算术平方根(一般省略+),另一个是 .它们互为相反数.这两个平方根合起来记作 ,读作“正、负根号a”.
(a是非负数)
根号
a叫被开方数
读作:正、负根号a
意义:a的平方根(a≥0)
和为0
平方根的表示方法
讲授新课
典例精析
【例4】求下列各数的平方根:
(1) 64 ;(2) ;(3) 0.0004;(4)(-25)2 ;(5)11.
解:(1)因为 ( 8)2 = 64,所以 64的平方根是 8,即±±.
(2)因为 ( )2 =,所以的平方根是 ,即±±.
(4)因为 ( 25)2 =(-25)2,所以(-25)2的平方根是 25,即±±.
(5)11的平方根是±
(3)因为(0.02)2 = 0.0004, 所以 0.0004 的平方根是0.02,即±±.
讲授新课
探究:开平方
求一个数a的平方根的运算,叫做开平方,a叫做被开方数.
想一想:开平方与平方运算有什么关系呢?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
(a≥0)
(a≥0)
讲授新课
开平方运算
±3的平方是9,即
例如:
9的平方根是±3,即
平方运算
互为
逆运算
讲授新课
探究:与的关系
64
7.2
0
表示a的算术平方根,依据算术平方根的定义:
(a≥0)
.
想一想:(1)根据所学知识填一填,并说明理由.
;
;
;
;
讲授新课
2
3
0.5
2
3
0.5
a
0
-a
(a>0)
(a=0)
(a<0)
(2)填一填,并说说你的理由.
对于任意数a,一定等于a吗?
当a≥0时,=a
.
讲授新课
之间有什么关系?一定相等吗?
(3) 与
不一定相等,只有当a≥0时,它们才相等.
当a<0 时,没有意义.
讲授新课
练一练
1、若一个正数x的两个平方根分别为3a-5和1-2a,求2x+2的平方根.
解:由题意得(3a-5)+(1-2a)=0,
解得a=4.
∴3a-5=12-5=7
∴x=72=49
∴ 2x+2=2×49+2=100.
∴2x+2的平方根为±10.
当堂检测
1.化简的结果是( )
A.-4 B.4 C.±4 D.2
2.若,则a的值为( )
A.-9 B.9 C.-3 D.
3.要使式子有意义,则x的取值范围是( )
A.x>3 B.x<3 C.x≥-3 D.x≥3
B
D
B
4.下列说法正确的是( )
A.5是25的算术平方根 B.16是4的算术平方根
C.-6是(-6)2的算术平方根 D.0没有算术平方根
A
当堂检测
5.若一个数的算术平方根是7,那么这个数是 .
6.的算术平方根是 ;的算术平方根是 .
7.若,则 .
8.已知a,b满足(a-1)2+=0,则a+b= .
16
49
-1
当堂检测
10.若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
11.若x2=3,则 x= , 若=3,则x= .
±3
±
9.平方根等于本身的数是 ;
算术平方根等于它本身的数是 ;
算术平方根和平方根相等的数是 .
0
0和1
0
当堂检测
12.求下列各数的算术平方根:(1)25; (2);(3)10-6 ;(4)
解:(1)因为52=25,所以25的算术平方根是5, 即.
(4),22=4,所以的算术平方根是2.
(3)因为(10-3)2=10-6,所以10-6的算术平方根是10-3,即 10-3;
(2)因为,所以的算术平方根是,即.
当堂检测
13. 已知4x2=81,求x的值.
解:∵4x2=81,
∴x2=
∴x=±
∴x的值为±.
当堂检测
14.(1)已知y=,求x+y的值;
解:∵7-x≥0,x-7≥0,
∴x-7=0,x=7,
∴y=5,
∴x+y=12.
(2)若4a+1的算术平方根是3,求a的值.
解:∵4a+1的算术平方根是3,
∴4a+1=32=9,
∴a=2
当堂检测
15. 若=2,正数b的两个平方根分别是2c-1和-c+2,求a+b+c的平方根.
解:∵正数b的两个平方根分别是2c-1和-c+2,
∴2c-1-c+2=0.解得c=-1.
∴b=(-2-1)2=9.
∵ =2,
∴a=5.
∴a+b+c=5+9-1=13.
∴13的平方根是± .
当堂检测
解:设每块地板砖的边长为x m.由题意得
240x2=60,
∴x2=,
∴,
所以每块地板砖的边长是0.5 m.
16.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
课堂小结
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
0的算术平方根是0.
算术平方根:
中的双重非负性:
a≥0
课堂小结
平方根的性质
平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
谢 谢~
11.1 平方根
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1、理解算术平方根的概念,会用根号表示正数的算术平方根.
2、理解算术平方根的非负性.
3、通过平方运算求某些非负数的算术平方根.
4、掌握平方根的意义及性质.
5、理解平方根与算术平方根的联系与区别.
导入新课
自由下落物体的高度 (米)与下落时间 (秒)的关系为h=4.9t2 .有
一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:当h=10时 ,得19.6=4.9t2 ,
所以 t2=4
那t应为何值呢?
讲授新课
知识点一 算术平方根
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
若题中的面积变为下表中的数值,你能知道对应的正方形画布边长吗?
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
讲授新课
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根. a的算术平方根记为 ,读作“根号a”,a叫做被开方数.
0的算术平方根是0.
记作:
规定:
讲授新课
试一试:1.你能根据等式 122=144,说出144的的算术平方根是多少吗?并用等式表示出来.
144的算术平方根是12,即=12.
x时,就是2的算术平方根,即
y时,y就是3的算术平方根,即
w时,w就是5的算术平方根,即
z时,z就是4的算术平方根,即
2.试求出上面问题中的x、y、z、w的值.
非平方数的算术平方根只能用根号表示.
讲授新课
典例精析
解: (1)因为302=900, 所以900的算术平方根是30,即=30;
【例1】求下列各数的算术平方根:
(1) 900; (2) 1; (3) ; (4) 14.
(3)因为,所以的算术平方根是,即;
(2)因为12=1, 所以1的算术平方根是1,即=1;
(4)14的算术平方根是.
讲授新课
方法归纳
a的算术平方根
互为逆运算
求非负数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
是算术平方根的运算符号
x =
x2 = a
(x≥0)
算术平方根的求解方法
读作:根号a
讲授新课
练一练
1、计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
讲授新课
2.若一个数的算术平方根是 ,那么这个数是 ;
3. 的算术平方根是 ;
4. 的算术平方根是 ;
5.若 ,则 .
7
16
讲授新课
知识点二 算术平方根的性质
想一想:(1)负数有算术平方根吗?
只有非负数(正数和0)有算术平方根,负数没有算术平方根(即当a<0时,无意义).
(2)一个非负数的算术平方根可能是负数吗?
不可能,非负数的算术平方根是非负数.
讲授新课
算数平方根具有双重非负性.
(a≥0)
非负数
算术平方根的性质:
正数的算术平方根是正数;
0的算术平方根是0;
负数没有算术平方根.
知识归纳
讲授新课
典例精析
解: 因为|m-1| ≥0,≥0,又|m-1| +=0,
所以 |m-1| =0,=0,
所以m=1,n=-3,
所以m+n=1+(-3)=-2.
【例2】若|m-1| + =0,求m+n的值.
归纳:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
讲授新课
练一练
1.已知: 求X-3Y+4Z的值.
解:由题意得:
解得
讲授新课
知识点三 算术平方根的实际应用
解:将s=19.6代入公式
s=4.9t2,
得 t2 =4 ,
所以正数 t2 =(秒).
即铁球到达地面需要2秒.
做一做:自由下落物体下落的距离s(米)与下落时间t(秒)的关系为s=4.9.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
讲授新课
典例精析
【例3】如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为5.5米,地面固定点C到帐篷支撑竿底部B的距离是4.5米,则帐篷支撑竿的高是多少米?
所以帐篷支撑竿的高是米.
解:由题意得AC=5.5米,BC=4.5米,∠ABC=90°.
在Rt△ABC中,由勾股定理得
==(米)
讲授新课
练一练
h
d
1、“欲穷千里目,更上一层楼”,说的是登得高看得远.如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 ,其中R是地球半径,约等于6400 km.小丽站在海边的一块岩石上,眼睛离海平面的高度h为20 m,她观测到远处一艘船刚露出海平面,求此时d的值.
解:
由R=6400 km,h=0.02 km,得
讲授新课
知识点四 平方根的概念及其性质
(2)平方等于正数的数都有几个,它们有什么关系?
平方等于正数的数有2个,它们互为相反数.
想一想:(1)平方等于的数有几个 平方等于 0.64 的数呢
平方等于的数有2个,即和;
平方等于 0.64 的数也有2个,即±0.8.
讲授新课
知识归纳
一般地,如果一个数x的平方等于a,即x2= a,那么这个数x叫做a的平方根(也叫二次方根).
例如:(±4)2=16,则4和-4都是16的平方根;
即16的平方根是4和-4;其中,4还是16的算术平方根.
平方根的概念
讲授新课
议一议:(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?
(3)因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
平方根的性质:一个正数有两个平方根(互为相反数);0只有一个平方根,它是0本身;负数没有平方根.
2个
1个
平方根如何表示呢?
讲授新课
知识归纳
正数a有两个平方根,一个是a的算术平方根(一般省略+),另一个是 .它们互为相反数.这两个平方根合起来记作 ,读作“正、负根号a”.
(a是非负数)
根号
a叫被开方数
读作:正、负根号a
意义:a的平方根(a≥0)
和为0
平方根的表示方法
讲授新课
典例精析
【例4】求下列各数的平方根:
(1) 64 ;(2) ;(3) 0.0004;(4)(-25)2 ;(5)11.
解:(1)因为 ( 8)2 = 64,所以 64的平方根是 8,即±±.
(2)因为 ( )2 =,所以的平方根是 ,即±±.
(4)因为 ( 25)2 =(-25)2,所以(-25)2的平方根是 25,即±±.
(5)11的平方根是±
(3)因为(0.02)2 = 0.0004, 所以 0.0004 的平方根是0.02,即±±.
讲授新课
探究:开平方
求一个数a的平方根的运算,叫做开平方,a叫做被开方数.
想一想:开平方与平方运算有什么关系呢?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
(a≥0)
(a≥0)
讲授新课
开平方运算
±3的平方是9,即
例如:
9的平方根是±3,即
平方运算
互为
逆运算
讲授新课
探究:与的关系
64
7.2
0
表示a的算术平方根,依据算术平方根的定义:
(a≥0)
.
想一想:(1)根据所学知识填一填,并说明理由.
;
;
;
;
讲授新课
2
3
0.5
2
3
0.5
a
0
-a
(a>0)
(a=0)
(a<0)
(2)填一填,并说说你的理由.
对于任意数a,一定等于a吗?
当a≥0时,=a
.
讲授新课
之间有什么关系?一定相等吗?
(3) 与
不一定相等,只有当a≥0时,它们才相等.
当a<0 时,没有意义.
讲授新课
练一练
1、若一个正数x的两个平方根分别为3a-5和1-2a,求2x+2的平方根.
解:由题意得(3a-5)+(1-2a)=0,
解得a=4.
∴3a-5=12-5=7
∴x=72=49
∴ 2x+2=2×49+2=100.
∴2x+2的平方根为±10.
当堂检测
1.化简的结果是( )
A.-4 B.4 C.±4 D.2
2.若,则a的值为( )
A.-9 B.9 C.-3 D.
3.要使式子有意义,则x的取值范围是( )
A.x>3 B.x<3 C.x≥-3 D.x≥3
B
D
B
4.下列说法正确的是( )
A.5是25的算术平方根 B.16是4的算术平方根
C.-6是(-6)2的算术平方根 D.0没有算术平方根
A
当堂检测
5.若一个数的算术平方根是7,那么这个数是 .
6.的算术平方根是 ;的算术平方根是 .
7.若,则 .
8.已知a,b满足(a-1)2+=0,则a+b= .
16
49
-1
当堂检测
10.若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
11.若x2=3,则 x= , 若=3,则x= .
±3
±
9.平方根等于本身的数是 ;
算术平方根等于它本身的数是 ;
算术平方根和平方根相等的数是 .
0
0和1
0
当堂检测
12.求下列各数的算术平方根:(1)25; (2);(3)10-6 ;(4)
解:(1)因为52=25,所以25的算术平方根是5, 即.
(4),22=4,所以的算术平方根是2.
(3)因为(10-3)2=10-6,所以10-6的算术平方根是10-3,即 10-3;
(2)因为,所以的算术平方根是,即.
当堂检测
13. 已知4x2=81,求x的值.
解:∵4x2=81,
∴x2=
∴x=±
∴x的值为±.
当堂检测
14.(1)已知y=,求x+y的值;
解:∵7-x≥0,x-7≥0,
∴x-7=0,x=7,
∴y=5,
∴x+y=12.
(2)若4a+1的算术平方根是3,求a的值.
解:∵4a+1的算术平方根是3,
∴4a+1=32=9,
∴a=2
当堂检测
15. 若=2,正数b的两个平方根分别是2c-1和-c+2,求a+b+c的平方根.
解:∵正数b的两个平方根分别是2c-1和-c+2,
∴2c-1-c+2=0.解得c=-1.
∴b=(-2-1)2=9.
∵ =2,
∴a=5.
∴a+b+c=5+9-1=13.
∴13的平方根是± .
当堂检测
解:设每块地板砖的边长为x m.由题意得
240x2=60,
∴x2=,
∴,
所以每块地板砖的边长是0.5 m.
16.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
课堂小结
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
0的算术平方根是0.
算术平方根:
中的双重非负性:
a≥0
课堂小结
平方根的性质
平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
谢 谢~
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
