11.6 二次根式的乘除法(同步课件)-八年级数学上册同步精品课堂(北京版)
文档属性
| 名称 | 11.6 二次根式的乘除法(同步课件)-八年级数学上册同步精品课堂(北京版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
11.6 二次根式的乘除法
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1.理解二次根式的乘法法则;
2.会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算;
3.了解二次根式的除法法则;
4.会运用除法法则及商的算术平方根进行简单运算;
5.能将二次根式化为最简二次根式.
温故知新
一、二次根式有哪些性质?
1.双重非负性:
2.一个非负数的算术平方根的平方等于它本身.
3.任意一个数的平方的算术平方根等于它本身的绝对值.
a (a≥0)
-a (a<0)
讲授新课
知识点一 二次根式乘法
活动1 计算下列各式,观察计算结果,你能发现什么规律
6
20
20
30
30
6
(a≥0,b≥0)
猜想
讲授新课
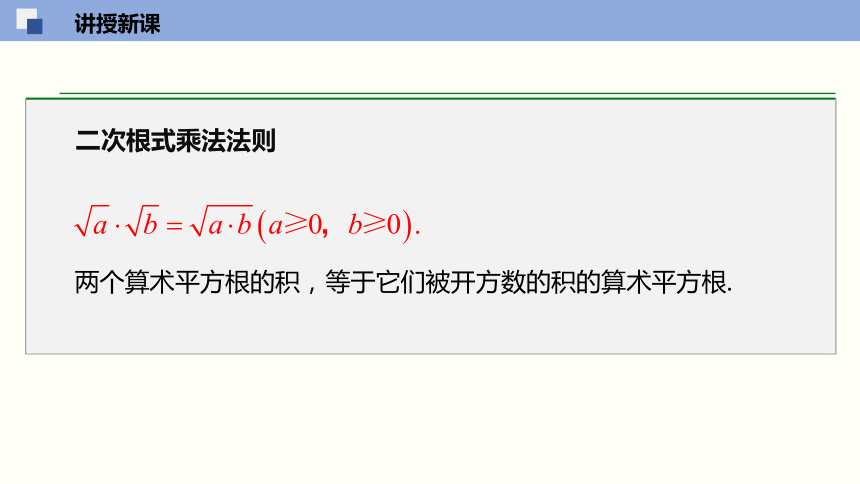
二次根式乘法法则
两个算术平方根的积,等于它们被开方数的积的算术平方根.
讲授新课
典例精析
【例1】计算:
解:
讲授新课
练一练
1、计算:
解:
讲授新课
知识点二 二次根式乘法的化简
反过来:
(a≥0,b≥0)
积的算术平方根的性质
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
(a≥0,b≥0)
一般的:
讲授新课
典例精析
解:(1) ;
【例2】化简:
(1) ;(2) .
(2)
讲授新课
练一练
1、化简:
解:
讲授新课
2、计算:
(1) ;(2) ; (3) .
解:(1)
(2)
(3)
讲授新课
知识点三 二次根式的除法
活动1 计算下列各式,观察计算结果,你能发现什么规律
猜想
(a≥0,b>0)
讲授新课
二次根式除法法则
两个算术平方根的商,等于各个被开方数相除商的算数平方根.
(a≥0,b>0)
讲授新课
二次根式除法法则
(a≥0,b>0)
(a≥0,b>0)
讲授新课
1.二次根式除法法则
2.商的算术平方根的性质
(a≥0,b>0)
(a≥0,b>0)
讲授新课
典例精析
【例3】计算:
解:
讲授新课
练一练
1、计算:
解:
(1)原式=
(2)原式=
(3)原式=
(4)原式=
讲授新课
我们可以运用它来进行二次根式的解题和化简.
语言表述:商的算术平方根,等于积中各因式的算术平方根的商.
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似的,把二次根式的除法法则反过来,就得到
二次根式的商的算术平方根的性质:
讲授新课
知识点四 二次根式化简计算
解:
计算.
讲授新课
, ,使分母中不含二次根式,并且被开方数中不含分母
解:
=
=
=
=
=
活动2 观察以上各题中,化简后的二次根式有什么特点
有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
满足上述两个条件的二次根式,叫做最简二次根式.
讲授新课
3.满足下列两个条件的二次根式,叫做最简二次根式
(1) 被开方数不含分母;
(2) 被开方数中不含能开得尽方的因数或因式.
简记:一根号无分母,分母无根号;二不能再开方.
讲授新课
【例4】把下列二次根式化成最简二次根式
解:
讲授新课
典例精析
【例4】把下列二次根式化成最简二次根式:
解:
讲授新课
练一练
1、计算:
解:(1)原式
.
(2)原式
.
当堂检测
1.计算×的结果为( )
A.2 B.4 C.2 D.4
2.下列计算正确的是( )
A.×2=6 B.5×5=5
C.4×2=6 D.4×2=8
3.下列各式化简后的结果为3的是( )
A. B. C. D.
B
D
C
当堂检测
4.下列式子中,属于最简二次根式的是( )
A. B. C. D.
5.的倒数是( )
A. B. C. D.
6.若成立,则的值可以是( )
A.-4 B.2 C.4 D.5
B
A
B
当堂检测
7.当时,化简的结果是( )
A. B. C. D.
8.把根号外面的因式移到根号内得( )
A. B. C. D.-1
A
C
当堂检测
9.二次根式 中,最简二次根式是
______________.
10.已知长方形的面积是48cm2, 其中一边的长是cm ,则另一边的长是______cm.
当堂检测
11.计算
(1); (2).
解:(1)原式
;
(2)原式=
=
=
当堂检测
12.把下列二次根式化成最简二次根式:
解:
当堂检测
13.计算:
(1); (2)2×.
解:(1)原式=;
(2)原式=.
当堂检测
14.一个长方形的长和宽分别是 和 . 求这个长方形的面积.
解:
答:这个长方形的面积为 .
当堂检测
15.化简.
解:
当堂检测
16.计算.
解:
(1)原式
(2)原式
(3)原式
当堂检测
17.若与是被开方数相同的最简二次根式,求的值.
解:∵ 与是被开方数相同的最简二次根式.
解得:
∴符合题意
.
课堂小结
算术平方根
二次根式乘除
乘法
除法
最简二次根式
谢 谢~
11.6 二次根式的乘除法
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1.理解二次根式的乘法法则;
2.会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算;
3.了解二次根式的除法法则;
4.会运用除法法则及商的算术平方根进行简单运算;
5.能将二次根式化为最简二次根式.
温故知新
一、二次根式有哪些性质?
1.双重非负性:
2.一个非负数的算术平方根的平方等于它本身.
3.任意一个数的平方的算术平方根等于它本身的绝对值.
a (a≥0)
-a (a<0)
讲授新课
知识点一 二次根式乘法
活动1 计算下列各式,观察计算结果,你能发现什么规律
6
20
20
30
30
6
(a≥0,b≥0)
猜想
讲授新课
二次根式乘法法则
两个算术平方根的积,等于它们被开方数的积的算术平方根.
讲授新课
典例精析
【例1】计算:
解:
讲授新课
练一练
1、计算:
解:
讲授新课
知识点二 二次根式乘法的化简
反过来:
(a≥0,b≥0)
积的算术平方根的性质
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
(a≥0,b≥0)
一般的:
讲授新课
典例精析
解:(1) ;
【例2】化简:
(1) ;(2) .
(2)
讲授新课
练一练
1、化简:
解:
讲授新课
2、计算:
(1) ;(2) ; (3) .
解:(1)
(2)
(3)
讲授新课
知识点三 二次根式的除法
活动1 计算下列各式,观察计算结果,你能发现什么规律
猜想
(a≥0,b>0)
讲授新课
二次根式除法法则
两个算术平方根的商,等于各个被开方数相除商的算数平方根.
(a≥0,b>0)
讲授新课
二次根式除法法则
(a≥0,b>0)
(a≥0,b>0)
讲授新课
1.二次根式除法法则
2.商的算术平方根的性质
(a≥0,b>0)
(a≥0,b>0)
讲授新课
典例精析
【例3】计算:
解:
讲授新课
练一练
1、计算:
解:
(1)原式=
(2)原式=
(3)原式=
(4)原式=
讲授新课
我们可以运用它来进行二次根式的解题和化简.
语言表述:商的算术平方根,等于积中各因式的算术平方根的商.
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似的,把二次根式的除法法则反过来,就得到
二次根式的商的算术平方根的性质:
讲授新课
知识点四 二次根式化简计算
解:
计算.
讲授新课
, ,使分母中不含二次根式,并且被开方数中不含分母
解:
=
=
=
=
=
活动2 观察以上各题中,化简后的二次根式有什么特点
有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
满足上述两个条件的二次根式,叫做最简二次根式.
讲授新课
3.满足下列两个条件的二次根式,叫做最简二次根式
(1) 被开方数不含分母;
(2) 被开方数中不含能开得尽方的因数或因式.
简记:一根号无分母,分母无根号;二不能再开方.
讲授新课
【例4】把下列二次根式化成最简二次根式
解:
讲授新课
典例精析
【例4】把下列二次根式化成最简二次根式:
解:
讲授新课
练一练
1、计算:
解:(1)原式
.
(2)原式
.
当堂检测
1.计算×的结果为( )
A.2 B.4 C.2 D.4
2.下列计算正确的是( )
A.×2=6 B.5×5=5
C.4×2=6 D.4×2=8
3.下列各式化简后的结果为3的是( )
A. B. C. D.
B
D
C
当堂检测
4.下列式子中,属于最简二次根式的是( )
A. B. C. D.
5.的倒数是( )
A. B. C. D.
6.若成立,则的值可以是( )
A.-4 B.2 C.4 D.5
B
A
B
当堂检测
7.当时,化简的结果是( )
A. B. C. D.
8.把根号外面的因式移到根号内得( )
A. B. C. D.-1
A
C
当堂检测
9.二次根式 中,最简二次根式是
______________.
10.已知长方形的面积是48cm2, 其中一边的长是cm ,则另一边的长是______cm.
当堂检测
11.计算
(1); (2).
解:(1)原式
;
(2)原式=
=
=
当堂检测
12.把下列二次根式化成最简二次根式:
解:
当堂检测
13.计算:
(1); (2)2×.
解:(1)原式=;
(2)原式=.
当堂检测
14.一个长方形的长和宽分别是 和 . 求这个长方形的面积.
解:
答:这个长方形的面积为 .
当堂检测
15.化简.
解:
当堂检测
16.计算.
解:
(1)原式
(2)原式
(3)原式
当堂检测
17.若与是被开方数相同的最简二次根式,求的值.
解:∵ 与是被开方数相同的最简二次根式.
解得:
∴符合题意
.
课堂小结
算术平方根
二次根式乘除
乘法
除法
最简二次根式
谢 谢~
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
