11.7 二次根式的加减法(同步课件)-八年级数学上册同步精品课堂(北京版)
文档属性
| 名称 | 11.7 二次根式的加减法(同步课件)-八年级数学上册同步精品课堂(北京版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 08:58:54 | ||
图片预览








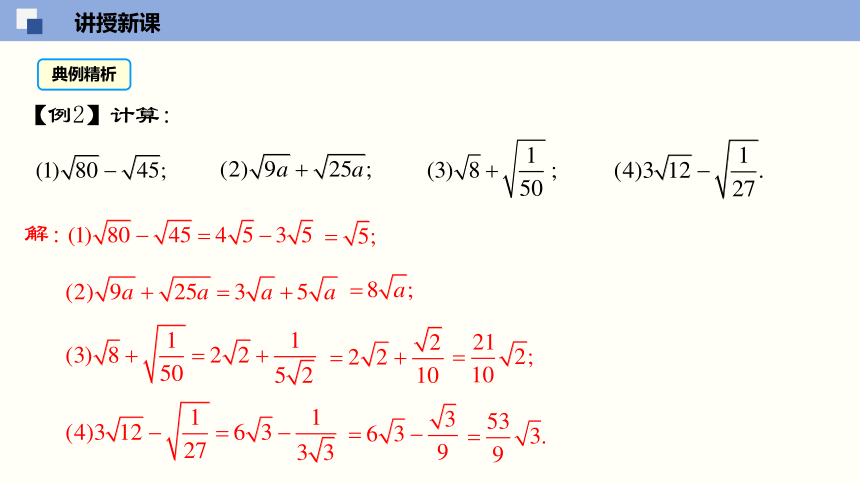
文档简介
(共37张PPT)
11.7 二次根式的加减法
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1.了解二次根式的加、减运算法则;
2.会用二次根式的加、减运算法则进行简单的运算;
3.掌握二次根式的混合运算的运算法则;
4.会运用二次根式的混合运算法则进行有关的运算;
温故知新
一、满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
简记为:一根号无分母,分母无根号;二不能再开方.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
导入新课
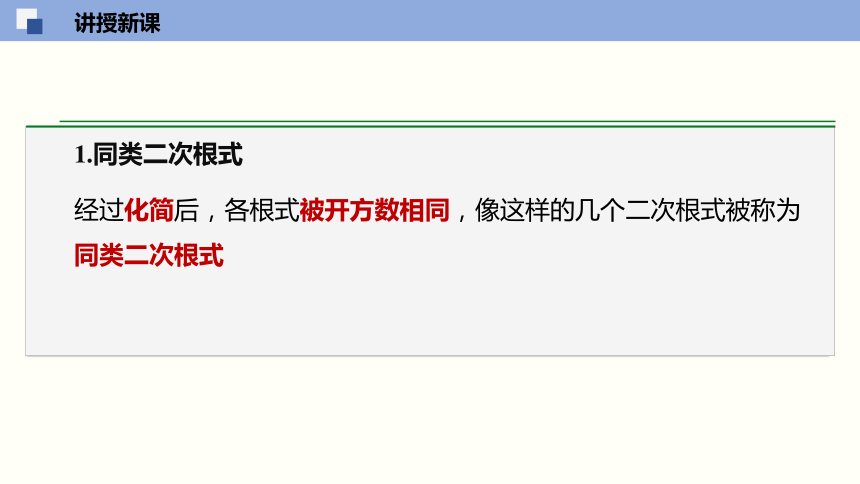
问题 现有一块长 7.5 dm、宽 5 dm 的木板,能否采用如图的方式,在这块木板上截出两个分别是 8 dm2 和 18 dm2 的正方形木板?
5 dm
5 dm
18
8
讲授新课
知识点一 同类二次根式
活动1 观察下列二次根式的被开数有什么共同特征:
每组的二次根式的被开方数相同
(1) ···
(2) ···
(3) ···
活动2 思考下列二次根式具有的被开数以上特征吗?你怎样发现的?:
讲授新课
1.同类二次根式
经过化简后,各根式被开方数相同,像这样的几个二次根式被称为同类二次根式
讲授新课
典例精析
【例1】下列各式中哪些是同类二次根式
讲授新课
练一练
1、若最简根式 与 可以合并,求 的值.
解:由题意得
解得
即
讲授新课
2、如果最简二次根式 和 是同类二次根式,求,的值.
解:由题意,得:,
解得: ,
∴,.
讲授新课
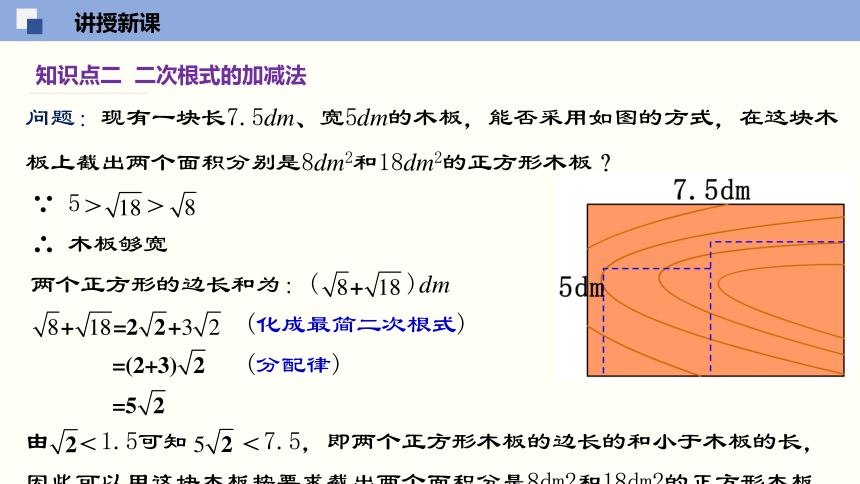
知识点二 二次根式的加减法
问题:现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
∵ 5> >
∴ 木板够宽
两个正方形的边长和为:( )dm
(化成最简二次根式)
(分配律)
由 <1.5可知 <7.5,即两个正方形木板的边长的和小于木板的长,
因此可以用这块木板按要求截出两个面积分是8dm2和18dm2的正方形木板.
讲授新课
(化成最简二次根式)
(分配律)
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式(同类二次根式)进行合并.
(1)化—将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找—找出被开方数相同的二次根式;
(3)并—把被开方数相同的二次根式合并.
“一化简二判断三合并”
讲授新课
典例精析
【例2】计算:
解:
讲授新课
练一练
2.计算:
解:
1.下列计算是否正确?为什么?
(1) ( ) (2) ( )
(3) ( ) (4) ( )
√
√
×
×
讲授新课
3、计算:
解:
讲授新课
4、计算:
解:
讲授新课
知识点三 二次根式的混合运算
【例3】计算:
解:
讲授新课
1、计算:
解:
讲授新课
解:(1)原式
(2)原式
2、计算:
讲授新课
3、计算:
解:
讲授新课
(1); (2).
4、计算:
(2)原式
.
解:(1)原式
;
讲授新课
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
如果分母不是单个的二次根式,而是含二次根式的式子,如:
等,该怎样去掉分母中的二次根式呢?
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
讲授新课
【例4】已知,,求的值.
解:∵,
,
∴
.
讲授新课
练一练
1、化简并求值:已知,求的值.
解:∵,
∴
.
讲授新课
知识点四 二次根式的应用
【例5】某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)求矩形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?
(1)解:矩形的长为米,宽为米,
∴矩形的周长为
(米).
答:矩形的周长为米.
讲授新课
(2)解:通道的面积为
(平方米),
则购买地砖需要花费(元).
答:购买地砖需要花费336元.
讲授新课
练一练
1、为了表示对老师的敬意,张昊同学特地做了两张大小不同的正方形的画送给老师,其中一张面积为800cm2,另一张面积为450cm2.他想:如果再用金色细彩带把画的边镶上会更漂亮.他手上现有1.2m长的金色细彩带.请你帮他算一算,他的金色细彩带够用吗?如果不够用,还需买多少厘米的金色细彩带?(≈1.414,结果保留整数)
解:镶壁画所用的金色彩带的长为:
4×(+)
=4×(20+15)
=140 ≈197.96(cm),
因为1.2m=120cm<197.96cm,
所以小号的金色彩带不够用.197.96-120=77.96≈78(cm),即还需买78cm的金色彩带.
当堂检测
1.下列各式中,与 是合并的二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则 m =_____.
1
3.下列二次根式,不能与 合并的是________(填 序号).
②⑤
当堂检测
4.估算的值是( )
A.和之间 B.和之间 C.和之间 D.和之间
5.若两个最简二次根式与可以合并,则合并后的结果是( )
A. B. C. D.
6.已知的整数部分是,小数部分是,则的值是( )
A. B. C.2 D.1
B
D
C
当堂检测
7.已知那么的大小关系是( )
A. B. C. D.
8.计算:_________.
9.已知,,则______.
10.对于任意的正数、定义运算“★”为:,则的运算结果为________.
C
4
当堂检测
11.计算:
(1); (2); (3).
(1)解:原式.
(2)解:原式
;
(3)解:原式
.
当堂检测
解:(1)原式=
=;
12.计算:
(1); (2);
(2)原式=
=
=;
当堂检测
(3)原式=
=
=
=;
(4)原式=
=
=.
(3); (4).
当堂检测
13.已知,,求的值.
解:∵,
,
∴
.
当堂检测
14.若最简二次根式与可以合并,求的算术平方根.
解:∵最简二次根式与可以合并,
∴与是同类二次根式,
∴,
解得,
∴,
∴,
即的算术平方根是5.
课堂小结
合并同类项
二次根式加减
同类二次根式
化简后,各根式被开方数相同
类比
法则
步骤
将二次根式化成最简二次根式,再将同类二次根式进行合并.
一化、二找、三合并
课堂小结
整式运算
二次根式混合运算
运算顺序
先算乘除,后算加减;有括号时,先算括号内的
类比
乘法公式
化简求值
平方差(a + b)(a - b) = a2- b2
完全平方(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
a2 + b2=(a + b)2 - 2ab2
=(a - b)2 +2ab.
谢 谢~
11.7 二次根式的加减法
数学(京改版)
八年级 上册
第十一章 实数和二次根式
学习目标
1.了解二次根式的加、减运算法则;
2.会用二次根式的加、减运算法则进行简单的运算;
3.掌握二次根式的混合运算的运算法则;
4.会运用二次根式的混合运算法则进行有关的运算;
温故知新
一、满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
简记为:一根号无分母,分母无根号;二不能再开方.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
导入新课
问题 现有一块长 7.5 dm、宽 5 dm 的木板,能否采用如图的方式,在这块木板上截出两个分别是 8 dm2 和 18 dm2 的正方形木板?
5 dm
5 dm
18
8
讲授新课
知识点一 同类二次根式
活动1 观察下列二次根式的被开数有什么共同特征:
每组的二次根式的被开方数相同
(1) ···
(2) ···
(3) ···
活动2 思考下列二次根式具有的被开数以上特征吗?你怎样发现的?:
讲授新课
1.同类二次根式
经过化简后,各根式被开方数相同,像这样的几个二次根式被称为同类二次根式
讲授新课
典例精析
【例1】下列各式中哪些是同类二次根式
讲授新课
练一练
1、若最简根式 与 可以合并,求 的值.
解:由题意得
解得
即
讲授新课
2、如果最简二次根式 和 是同类二次根式,求,的值.
解:由题意,得:,
解得: ,
∴,.
讲授新课
知识点二 二次根式的加减法
问题:现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
∵ 5> >
∴ 木板够宽
两个正方形的边长和为:( )dm
(化成最简二次根式)
(分配律)
由 <1.5可知 <7.5,即两个正方形木板的边长的和小于木板的长,
因此可以用这块木板按要求截出两个面积分是8dm2和18dm2的正方形木板.
讲授新课
(化成最简二次根式)
(分配律)
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式(同类二次根式)进行合并.
(1)化—将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找—找出被开方数相同的二次根式;
(3)并—把被开方数相同的二次根式合并.
“一化简二判断三合并”
讲授新课
典例精析
【例2】计算:
解:
讲授新课
练一练
2.计算:
解:
1.下列计算是否正确?为什么?
(1) ( ) (2) ( )
(3) ( ) (4) ( )
√
√
×
×
讲授新课
3、计算:
解:
讲授新课
4、计算:
解:
讲授新课
知识点三 二次根式的混合运算
【例3】计算:
解:
讲授新课
1、计算:
解:
讲授新课
解:(1)原式
(2)原式
2、计算:
讲授新课
3、计算:
解:
讲授新课
(1); (2).
4、计算:
(2)原式
.
解:(1)原式
;
讲授新课
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
如果分母不是单个的二次根式,而是含二次根式的式子,如:
等,该怎样去掉分母中的二次根式呢?
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
讲授新课
【例4】已知,,求的值.
解:∵,
,
∴
.
讲授新课
练一练
1、化简并求值:已知,求的值.
解:∵,
∴
.
讲授新课
知识点四 二次根式的应用
【例5】某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)求矩形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?
(1)解:矩形的长为米,宽为米,
∴矩形的周长为
(米).
答:矩形的周长为米.
讲授新课
(2)解:通道的面积为
(平方米),
则购买地砖需要花费(元).
答:购买地砖需要花费336元.
讲授新课
练一练
1、为了表示对老师的敬意,张昊同学特地做了两张大小不同的正方形的画送给老师,其中一张面积为800cm2,另一张面积为450cm2.他想:如果再用金色细彩带把画的边镶上会更漂亮.他手上现有1.2m长的金色细彩带.请你帮他算一算,他的金色细彩带够用吗?如果不够用,还需买多少厘米的金色细彩带?(≈1.414,结果保留整数)
解:镶壁画所用的金色彩带的长为:
4×(+)
=4×(20+15)
=140 ≈197.96(cm),
因为1.2m=120cm<197.96cm,
所以小号的金色彩带不够用.197.96-120=77.96≈78(cm),即还需买78cm的金色彩带.
当堂检测
1.下列各式中,与 是合并的二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则 m =_____.
1
3.下列二次根式,不能与 合并的是________(填 序号).
②⑤
当堂检测
4.估算的值是( )
A.和之间 B.和之间 C.和之间 D.和之间
5.若两个最简二次根式与可以合并,则合并后的结果是( )
A. B. C. D.
6.已知的整数部分是,小数部分是,则的值是( )
A. B. C.2 D.1
B
D
C
当堂检测
7.已知那么的大小关系是( )
A. B. C. D.
8.计算:_________.
9.已知,,则______.
10.对于任意的正数、定义运算“★”为:,则的运算结果为________.
C
4
当堂检测
11.计算:
(1); (2); (3).
(1)解:原式.
(2)解:原式
;
(3)解:原式
.
当堂检测
解:(1)原式=
=;
12.计算:
(1); (2);
(2)原式=
=
=;
当堂检测
(3)原式=
=
=
=;
(4)原式=
=
=.
(3); (4).
当堂检测
13.已知,,求的值.
解:∵,
,
∴
.
当堂检测
14.若最简二次根式与可以合并,求的算术平方根.
解:∵最简二次根式与可以合并,
∴与是同类二次根式,
∴,
解得,
∴,
∴,
即的算术平方根是5.
课堂小结
合并同类项
二次根式加减
同类二次根式
化简后,各根式被开方数相同
类比
法则
步骤
将二次根式化成最简二次根式,再将同类二次根式进行合并.
一化、二找、三合并
课堂小结
整式运算
二次根式混合运算
运算顺序
先算乘除,后算加减;有括号时,先算括号内的
类比
乘法公式
化简求值
平方差(a + b)(a - b) = a2- b2
完全平方(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2.
a2 + b2=(a + b)2 - 2ab2
=(a - b)2 +2ab.
谢 谢~
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
