24.2.2.2 切线的判定课件人教版数学九年级上册
文档属性
| 名称 | 24.2.2.2 切线的判定课件人教版数学九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 08:58:54 | ||
图片预览





文档简介
(共27张PPT)
第二十四章 圆
24.2.2.2 切线的判定
Date:2024.10.28
学习目标
1. 会判定一条直线是否是圆的切线,并会过圆上一点
作圆的切线;
2. 理解并掌握圆的切线的判定定理;(重点)
3. 能运用圆的切线的判定定理解决问题. (难点)
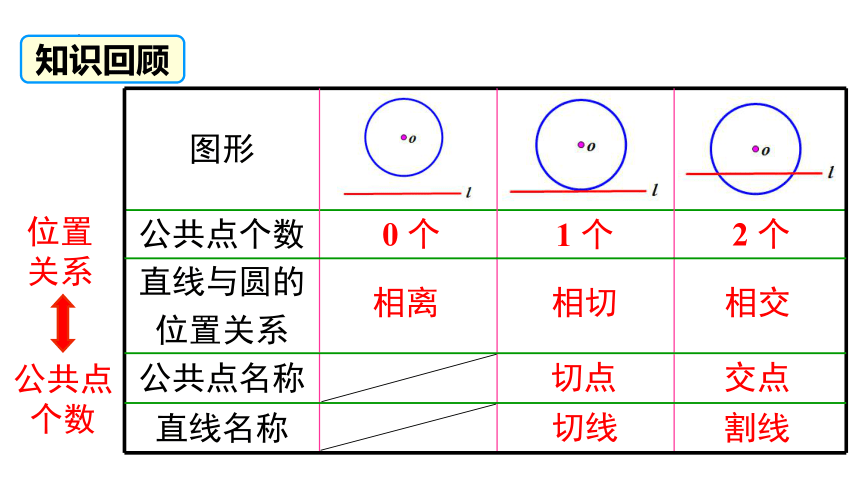
知识回顾
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
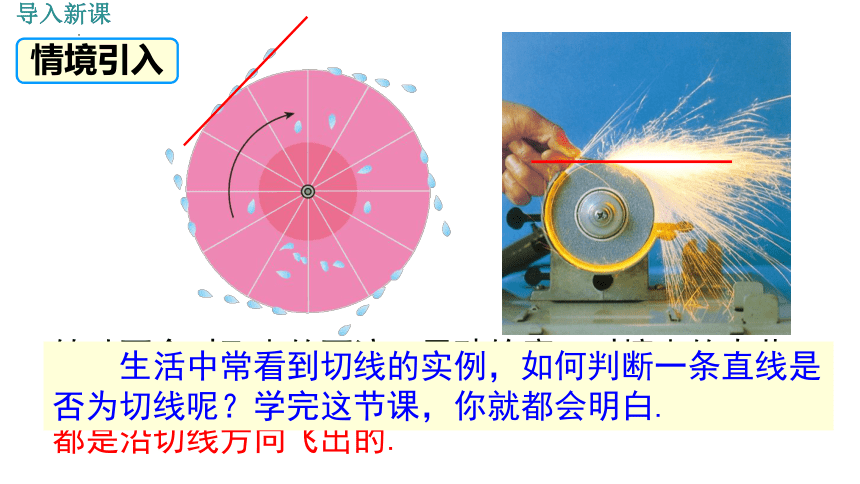
导入新课
情境引入
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
A
B
C
问题:已知圆 O 上一点 A,怎样根据圆的切线定义过点 A 作圆 O 的切线?
观察:
(1) 圆心 O 到直线 AB 的距离和圆的
半径有什么数量关系
(2)二者位置有什么关系?为什么?
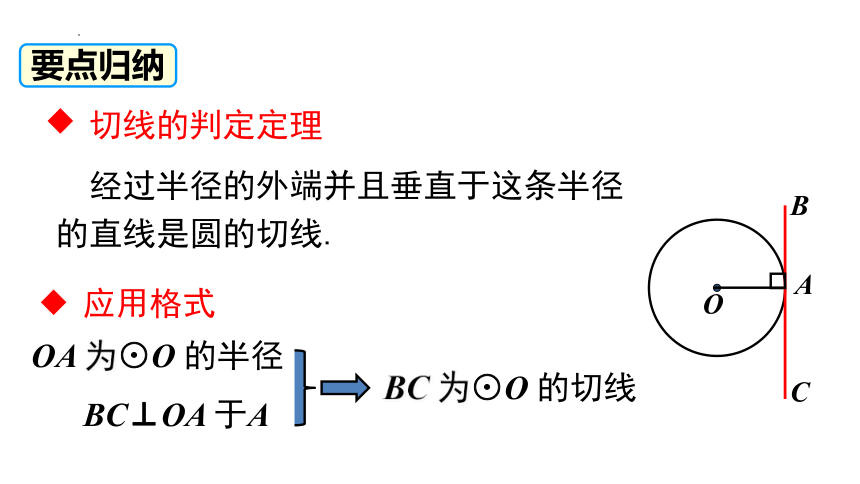
切线的判定定理
一
O
讲授新课
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为⊙O 的半径
BC⊥OA 于A
BC 为⊙O 的切线
A
B
C
切线的判定定理
应用格式
O
要点归纳
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
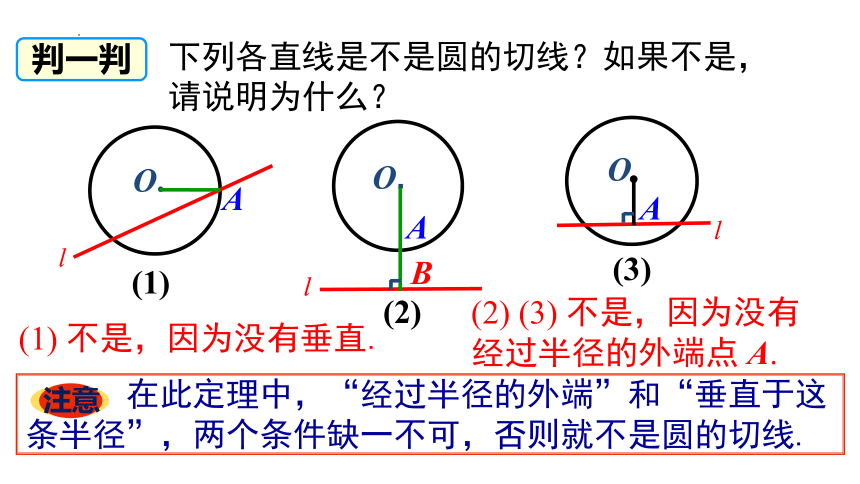
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1) 不是,因为没有垂直.
(2) (3) 不是,因为没有经过半径的外端点 A.
判一判
注意
O.
A
O.
A
B
A
O
(1)
(2)
(3)
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r)时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
要点归纳
O
O
【例1】(教材P98.T1)如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线.
证明:∵∠ABT=45°,AT=AB,
∴∠ATB=∠ABT=45°.
∴∠BAT=90°.
∴AT是⊙O的切线.
分析:直线 AC 经过半径的一端,因此只要证 OA 垂直于 AC 即可.
【变式1】如图,线段AB经过圆心O,交⊙O于点A,C,AD为⊙O的弦,连接BD,∠BAD=∠B=30°.求证:BD是⊙O的切线.
证明:连接OD.
∵OA=OD,∠A=∠ABD=30°,
∴∠A=∠ADO=30°.
∴∠DOB=∠A+∠ADO=60°.
∴∠ODB=180°-∠DOB-∠B=90°.
∵OD是半径,
∴BD是⊙O的切线.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
方法总结
例2 已知直线 AB 经过 ⊙O 上的点 C,并且 OA = OB,
CA = CB. 求证:直线 AB 是 ⊙O 的切线.
O
B
A
C
证明:连接 OC.
∵ OA = OB,CA = CB,
∴ OC 是等腰△OAB 底边 AB 上的中线.
∴ OC⊥AB.
∵ OC 是 ⊙O 的半径,
∴ AB 是 ⊙O 的切线.
分析:由于 AB 过⊙O 上的点 C,所以连接 OC,只要
证明 AB⊥OC 即可.
【变式2】.如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN于点E.求证:DE是⊙O的切线.
证明:如图,连接OD.
∵OA=OD,
∴∠1=∠2.
∵AD平分∠CAM,
∴∠2=∠3.
∴∠1=∠3.
∴MN∥OD.
∵DE⊥MN,
∴DE⊥OD.
∵OD是⊙O的半径,
∴DE是⊙O的切线.
例3 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
B
C
D
A
E
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB = r.
∴ AC 是⊙O 的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线段,证明垂线段等于半径,即可得出已知直线为圆的切线.
方法总结
【变式3】如图,△ABC为等腰三角形,点O是底边BC的中点,过点O作OD⊥AB于点D,以点O为圆心,OD的长为半径作⊙O.求证:AC是⊙O的切线.
证明:如图,连接OA,
作OF⊥AC于点F.
∵△ABC为等腰三角形,
点O是底边BC的中点,
∴AO⊥BC,
AO平分∠BAC.
∵OD⊥AB,OF⊥AC,
∴OF=OD.
∴OF为⊙O的半径.
∴AC是⊙O的切线.
(1) 有交点,连半径,证垂直;
证切线时辅助线的添加方法
要点归纳
(2) 无交点,作垂直,证半径.
例3
例2
课堂小结
这节课,你学到了什么?
切线的判定(1) 切线的判定(2)
文字描述 若圆心到直线的距离(d)________半径(r),则这条直线是圆的切线. 经过半径的________并且________这条半径的直线是圆的切线.
图形 OA=OB=5, AB=8, ⊙O的半径为3.
几何语言 ∵________________, ∴AB是⊙O的切线. ∵_______________________,
∴AB是⊙O的切线.
口诀 无切点,作垂直(d),证半径(d=r). 有切点,连半径,证垂直.
等于
外端
垂直
OC=3
OA是⊙O的半径,OA⊥l
1.如图,OA是⊙O的半径,∠B=25°,∠AOB=65°.求证:AB是⊙O的切线.
证明:∵∠B=25°,∠AOB=65°,
∴∠OAB=90°.
∴OA⊥AB.
∵OA是⊙O的半径,
∴AB是⊙O的切线.
课堂检测
2.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
证明:如图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
又∵OC是⊙O的半径,
∴直线AB是⊙O的切线.
3.如图,点D是∠AOB的平分线OC上任意一点,过点D作DE⊥OB于点E,以DE为半径作⊙D.求证:OA是⊙D的切线.
证明:如图,过点D作DF⊥OA于点F.
∵点D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,即D到直线OA的距离等于⊙D的半径DE.
∴⊙D与OA相切.
即OA是⊙O的切线.
4.如图,AB是⊙O的一条弦,点E是劣弧AB的中点,直线CD经过点E且与直线AB平行.求证:直线CD是⊙O的切线.
证明:如图,连接OE交AB于点F.
∵点E是劣弧AB的中点,
∴OE⊥AB.
∵AB∥CD,
∴CD⊥OE.
∵OE是⊙O的半径,
∴直线CD是⊙O的切线.
5.如图,在△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD长为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
解:(1)证明:如图,过点D作DF⊥AC于点F.
∵∠B=90°,
∴AB⊥BC.
∵CD平分∠ACB交AB于点D,
∴BD=DF.
∴⊙D与AC相切.
6.如图,在△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD长为半径作⊙D交AB于点E.
(2)若AC=5,BC=3,试求AE的长.
解:(2)设圆的半径为r.
∵∠B=90°,BC=3,AC=5,
∴AB==4.
∵DB=DF,CD=CD,
∴Rt△CDF≌Rt△CDB.
∴BC=FC=3.
∴AF=AC-CF=2.
∵AB=4,
∴AD=AB-BD=4-r.
在Rt△AFD中,
(4-r)2=r2+22,解得r=.
∴AE=4-3=1.
7.如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,判断直线DE与⊙O的位置关系,并说明理由.
解:直线DE与⊙O相切.理由如下:
如图,连接OD,AD.
∵AB为⊙O的直径,
∴∠ADB=90°.
∴△ADC为直角三角形.
∵点E是AC的中点,
∴ED=EA.
∴∠EAD=∠EDA.
∵OA=OD,
∴∠OAD=∠ODA.
∴∠EAD+∠OAD=∠EDA+∠ODA.
∴∠EDO=∠EAO=90°.
∴ED⊥OD.
∴DE为⊙O的切线.
作业布置
课堂练习
PS.希望大家认真细致完成作业!
第二十四章 圆
24.2.2.2 切线的判定
Date:2024.10.28
学习目标
1. 会判定一条直线是否是圆的切线,并会过圆上一点
作圆的切线;
2. 理解并掌握圆的切线的判定定理;(重点)
3. 能运用圆的切线的判定定理解决问题. (难点)
知识回顾
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
导入新课
情境引入
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
A
B
C
问题:已知圆 O 上一点 A,怎样根据圆的切线定义过点 A 作圆 O 的切线?
观察:
(1) 圆心 O 到直线 AB 的距离和圆的
半径有什么数量关系
(2)二者位置有什么关系?为什么?
切线的判定定理
一
O
讲授新课
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为⊙O 的半径
BC⊥OA 于A
BC 为⊙O 的切线
A
B
C
切线的判定定理
应用格式
O
要点归纳
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1) 不是,因为没有垂直.
(2) (3) 不是,因为没有经过半径的外端点 A.
判一判
注意
O.
A
O.
A
B
A
O
(1)
(2)
(3)
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r)时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
要点归纳
O
O
【例1】(教材P98.T1)如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线.
证明:∵∠ABT=45°,AT=AB,
∴∠ATB=∠ABT=45°.
∴∠BAT=90°.
∴AT是⊙O的切线.
分析:直线 AC 经过半径的一端,因此只要证 OA 垂直于 AC 即可.
【变式1】如图,线段AB经过圆心O,交⊙O于点A,C,AD为⊙O的弦,连接BD,∠BAD=∠B=30°.求证:BD是⊙O的切线.
证明:连接OD.
∵OA=OD,∠A=∠ABD=30°,
∴∠A=∠ADO=30°.
∴∠DOB=∠A+∠ADO=60°.
∴∠ODB=180°-∠DOB-∠B=90°.
∵OD是半径,
∴BD是⊙O的切线.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
方法总结
例2 已知直线 AB 经过 ⊙O 上的点 C,并且 OA = OB,
CA = CB. 求证:直线 AB 是 ⊙O 的切线.
O
B
A
C
证明:连接 OC.
∵ OA = OB,CA = CB,
∴ OC 是等腰△OAB 底边 AB 上的中线.
∴ OC⊥AB.
∵ OC 是 ⊙O 的半径,
∴ AB 是 ⊙O 的切线.
分析:由于 AB 过⊙O 上的点 C,所以连接 OC,只要
证明 AB⊥OC 即可.
【变式2】.如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN于点E.求证:DE是⊙O的切线.
证明:如图,连接OD.
∵OA=OD,
∴∠1=∠2.
∵AD平分∠CAM,
∴∠2=∠3.
∴∠1=∠3.
∴MN∥OD.
∵DE⊥MN,
∴DE⊥OD.
∵OD是⊙O的半径,
∴DE是⊙O的切线.
例3 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
B
C
D
A
E
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB = r.
∴ AC 是⊙O 的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线段,证明垂线段等于半径,即可得出已知直线为圆的切线.
方法总结
【变式3】如图,△ABC为等腰三角形,点O是底边BC的中点,过点O作OD⊥AB于点D,以点O为圆心,OD的长为半径作⊙O.求证:AC是⊙O的切线.
证明:如图,连接OA,
作OF⊥AC于点F.
∵△ABC为等腰三角形,
点O是底边BC的中点,
∴AO⊥BC,
AO平分∠BAC.
∵OD⊥AB,OF⊥AC,
∴OF=OD.
∴OF为⊙O的半径.
∴AC是⊙O的切线.
(1) 有交点,连半径,证垂直;
证切线时辅助线的添加方法
要点归纳
(2) 无交点,作垂直,证半径.
例3
例2
课堂小结
这节课,你学到了什么?
切线的判定(1) 切线的判定(2)
文字描述 若圆心到直线的距离(d)________半径(r),则这条直线是圆的切线. 经过半径的________并且________这条半径的直线是圆的切线.
图形 OA=OB=5, AB=8, ⊙O的半径为3.
几何语言 ∵________________, ∴AB是⊙O的切线. ∵_______________________,
∴AB是⊙O的切线.
口诀 无切点,作垂直(d),证半径(d=r). 有切点,连半径,证垂直.
等于
外端
垂直
OC=3
OA是⊙O的半径,OA⊥l
1.如图,OA是⊙O的半径,∠B=25°,∠AOB=65°.求证:AB是⊙O的切线.
证明:∵∠B=25°,∠AOB=65°,
∴∠OAB=90°.
∴OA⊥AB.
∵OA是⊙O的半径,
∴AB是⊙O的切线.
课堂检测
2.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
证明:如图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
又∵OC是⊙O的半径,
∴直线AB是⊙O的切线.
3.如图,点D是∠AOB的平分线OC上任意一点,过点D作DE⊥OB于点E,以DE为半径作⊙D.求证:OA是⊙D的切线.
证明:如图,过点D作DF⊥OA于点F.
∵点D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,即D到直线OA的距离等于⊙D的半径DE.
∴⊙D与OA相切.
即OA是⊙O的切线.
4.如图,AB是⊙O的一条弦,点E是劣弧AB的中点,直线CD经过点E且与直线AB平行.求证:直线CD是⊙O的切线.
证明:如图,连接OE交AB于点F.
∵点E是劣弧AB的中点,
∴OE⊥AB.
∵AB∥CD,
∴CD⊥OE.
∵OE是⊙O的半径,
∴直线CD是⊙O的切线.
5.如图,在△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD长为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
解:(1)证明:如图,过点D作DF⊥AC于点F.
∵∠B=90°,
∴AB⊥BC.
∵CD平分∠ACB交AB于点D,
∴BD=DF.
∴⊙D与AC相切.
6.如图,在△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD长为半径作⊙D交AB于点E.
(2)若AC=5,BC=3,试求AE的长.
解:(2)设圆的半径为r.
∵∠B=90°,BC=3,AC=5,
∴AB==4.
∵DB=DF,CD=CD,
∴Rt△CDF≌Rt△CDB.
∴BC=FC=3.
∴AF=AC-CF=2.
∵AB=4,
∴AD=AB-BD=4-r.
在Rt△AFD中,
(4-r)2=r2+22,解得r=.
∴AE=4-3=1.
7.如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,判断直线DE与⊙O的位置关系,并说明理由.
解:直线DE与⊙O相切.理由如下:
如图,连接OD,AD.
∵AB为⊙O的直径,
∴∠ADB=90°.
∴△ADC为直角三角形.
∵点E是AC的中点,
∴ED=EA.
∴∠EAD=∠EDA.
∵OA=OD,
∴∠OAD=∠ODA.
∴∠EAD+∠OAD=∠EDA+∠ODA.
∴∠EDO=∠EAO=90°.
∴ED⊥OD.
∴DE为⊙O的切线.
作业布置
课堂练习
PS.希望大家认真细致完成作业!
同课章节目录
