人教版:2024-2025八年级数学期中模拟试卷1(含答案解析)
文档属性
| 名称 | 人教版:2024-2025八年级数学期中模拟试卷1(含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 08:39:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年八年级(上)期中数学试卷模拟1
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列会徽中,不是轴对称图形的是( )
A. B. C. D.
2.一个多边形的每一个内角都是135°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.下列说法正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等三角形一定关于某条直线对称
C.两图形关于某条直线对称,则这两个图形一定分别位于对称轴的两侧
D.有一条公共边的两个全等三角形关于公共边的所在的直线对称
4.如图,已知∠1+2+∠3+∠4=280°,那么∠5的度数为( )
A.70° B.80° C.90° D.100°
5.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
6.一个多边形的内角和是外角和的四倍,它是几边形?( )
A.四 B.六 C.八 D.十
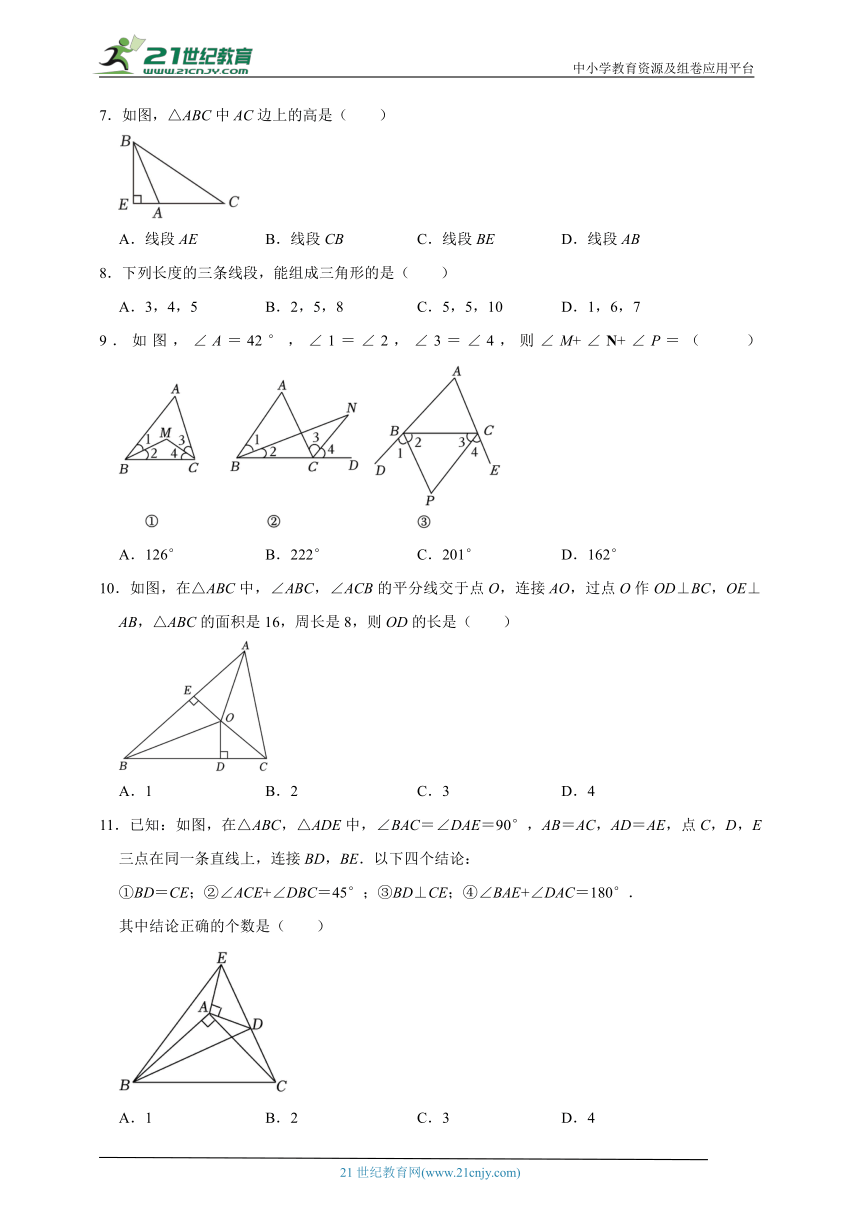
7.如图,△ABC中AC边上的高是( )
A.线段AE B.线段CB C.线段BE D.线段AB
8.下列长度的三条线段,能组成三角形的是( )
A.3,4,5 B.2,5,8 C.5,5,10 D.1,6,7
9.如图,∠A=42°,∠1=∠2,∠3=∠4,则∠M+∠N+∠P=( )
A.126° B.222° C.201° D.162°
10.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,连接AO,过点O作OD⊥BC,OE⊥AB,△ABC的面积是16,周长是8,则OD的长是( )
A.1 B.2 C.3 D.4
11.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
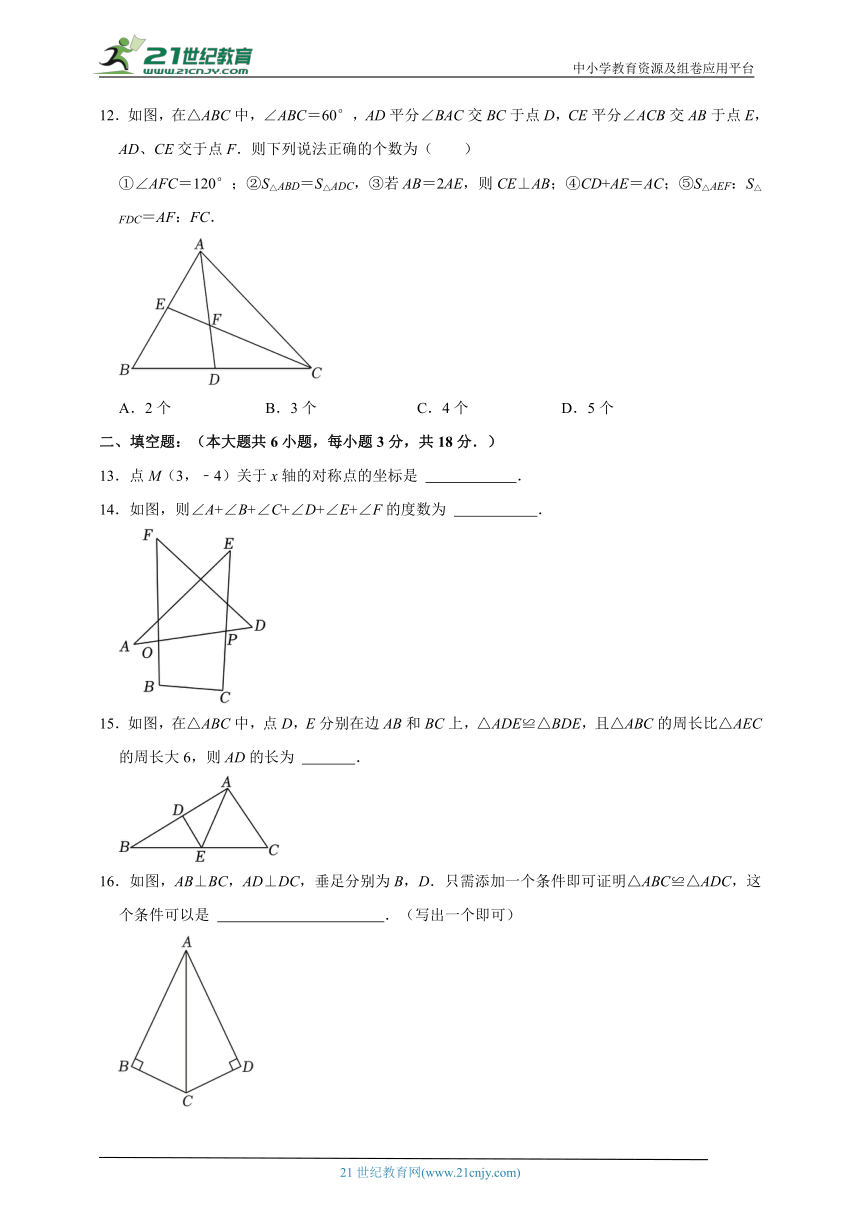
12.如图,在△ABC中,∠ABC=60°,AD平分∠BAC交BC于点D,CE平分∠ACB交AB于点E,AD、CE交于点F.则下列说法正确的个数为( )
①∠AFC=120°;②S△ABD=S△ADC,③若AB=2AE,则CE⊥AB;④CD+AE=AC;⑤S△AEF:S△FDC=AF:FC.
A.2个 B.3个 C.4个 D.5个
二、填空题:(本大题共6小题,每小题3分,共18分.)
13.点M(3,﹣4)关于x轴的对称点的坐标是 .
14.如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
15.如图,在△ABC中,点D,E分别在边AB和BC上,△ADE≌△BDE,且△ABC的周长比△AEC的周长大6,则AD的长为 .
16.如图,AB⊥BC,AD⊥DC,垂足分别为B,D.只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
17.如图,在△ABC中,∠BAC=45°,高AD,CE交于点H.若AB=12,CE=7,则CH= .
18.如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连接GC,使∠G=∠BAD.下列结论中正确的有 .(写序号)
①BE=CF;②AG=2DE;③S△ABD+S△CDF=S△GCF;④S△AGC=2S△BDE.
三、解答题:(本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.)
19. C在直角坐标系内的位置如图所示:
(1)分别写出点A,C的坐标:A的坐标: ,C的坐标: ;
(2)请在这个坐标系内画出与△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标 ;
(3)求△A1B1C1的面积.
20个多边形的内角和是它的外角和的3倍,求这个多边形的边数.
21知△ABC的三边长是a,b,c.
(1)若a=6,b=8,且三角形的周长是小于22的偶数,求c的值;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
22,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E.
(1)若∠C=52°,∠BAC=68°,求∠ADB的度数;
(2)若∠BED=57°,求∠C的度数.
23图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC、BF交于E,∠FEC=110°.
(1)求∠FAC的度数;
(2)AF平行于DC吗?说明理由;
(3)求∠BAC的度数.
24. 两个三角形纸板△ABC和△DBE按如图所示的方式摆放,连接DC.已知BA=DB,BE=BC,AC=DE=DC.
(1)求证:△ABC≌△DBE;
(2)若∠ACD=72°,求∠BED的度数.
25.如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6.(1)若∠DBO=20°,则∠DAC= ;
(2)求BO的长;
(3)F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P、Q两点同时停止运动,设运动时间为t(秒),当△AOP与△FCQ全等时,直接写出t的值.
答案解析
一、选择题
答案解析
一、选择题
1.【解答】解:A、B、D中图形,都能找到一条直线,折叠后直线两旁的部分重合,所以是轴对称图形;C中图形,不能找到一条直线,折叠后直线两旁的部分重合,所以不是轴对称图形.故选:C.
2.【解答】解:多边形的边数是:n=360÷(180﹣135)=8.故选:B.
3.【解答】解:A、关于某直线对称的两个三角形是全等三角形,正确,符合题意;
B、全等三角形是关于某直线对称的错误,例如图一,错误,不符合题意;
C、两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧错误,例如图二:错误,不符合题意;
D、有一条公共边的两个全等三角形关于公共边所在的直线对称,错误,例如图三,不符合题意,
故选:A.
4.【解答】解:由题意得:∠1+2+∠3+∠4+∠5=360°,∵∠1+2+∠3+∠4=280°,
∴∠5=360°﹣280°=80°,故选:B.
5.【解答】解:做法中用到的三角形全等的判定方法是SSS
证明如下:由题意得,PN=PM,在△ONP和△OMP中,
,
∴△ONP≌△OMP(SSS)所以∠NOP=∠MOP故OP为∠AOB的平分线.故选:A.
6. 【解答】解:设这个多边形是n边形,则(n﹣2)×180°=4×360°,整理得:n﹣2=8,
解得:n=10,即这个多边形是十边形.故选:D.
7.【解答】解:△ABC中AC边上的高是线段BE.故选:C.
8.【解答】解:A、3+4>5,故能构成三角形,故此选项符合题意;
B、2+5<8,故不能构成三角形,故此选项不符合题意;
C、5+5=10,故不能构成三角形,故此选项不符合题意;
D、1+6=7,故不能构成三角形,故此选项不符合题意.故选:A.
9. 【解答】解:图1:∵在△ABC中,∠A=60°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣42°=138°,∵∠1=∠2,∠3=∠4,∴,,
∴∠2+∠4==69°,∴∠M=180°﹣(∠2+∠4)=180°﹣69°=111°;
图2:∵∠ACD是△ABC的外角,∠A=42°,∴∠ACD=∠A+∠ABC,
∵∠1=∠2,∠3=∠4,∴2∠4=2∠2+∠A,∵∠NCD是△NBC的外角,
∴∠4=∠NCD=∠N+∠2,∴=21°;
图3:
∵∠DBC是△ABC的外角,∠ECB是△ABC的外角,∠A=42°,
∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC
=∠A+(∠ACB+∠A+∠ABC)=42°+180°=222°,
又∵∠1=∠2,∠3=∠4,∴,,
∴∠2+∠3==111°,∴∠P=180°﹣(∠2+∠3)=180°﹣111°=69°,
∴∠M+∠N+∠P=111°+21°+69°=201°.
故选:C.
10.【解答】解:如图,过点O作OF⊥AC于F,∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OD=OE,
∵OC平分∠ACB,OD⊥BC,OF⊥AC,∴OD=OF,∴OD=OE=OF,
由题意得:AB OE+BC OD+AC OF=16,∴×8×OD=16,解得:OD=4,
故选:D.
11. 【解答】解:①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;
②∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°,
∵△BAD≌△CAE,∴∠ABD=∠ACE,∴∠ACE+∠DBC=45°,本选项正确;
③∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,本选项正确;
④∵∠BAC=∠DAE=90°,∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故此选项正确,
故选:D.
12. 【解答】解:①在△ABC中,∠ABC=60°,∴∠ACB+∠CAB=120°,
∵AD平分∠BAC,CE平分∠ACB,∴∠FCA=,∠FAC=CAB,
∴∠AFC=180°﹣(∠FCA+∠FAC)=180°﹣(∠ACB+∠CAB)=120°,故①正确;
②当AD是△ABC的中线时,S△ABD=S△ADC,而AD平分∠BAC,故②错误;
③如图,延长CE至G,使GE=CE,连接BG,∵AB=2AE,∴AE=BE,∵∠AEC=∠BEG,
∴△ACE≌△BGE(SAS),∴∠ACE=∠G,CE=GE,∵CE为角平分线,∴∠ACE=∠BCE,
∴∠BCE=∠G,∴BC=BG,∵CE=GE,∴BE⊥CE,故③正确;
④如图,作∠AFC的平分线交AC于点G,
由①得∠AFC=120°,∴∠AFG=∠CFG=60°,∴∠AFE=60°,
∴∠AFG=∠CFG=∠AFE=60°,∵∠EAF=∠GAF,∠DCF=∠GCF,
∴△AEF≌△AGF(ASA),△CDF≌△CGF(ASA),∴AE=AG,CD=CG,
∴CD+AE=CG+AG=AC,故④正确;
⑤过G作GM⊥FC,GH⊥AF于点G,H,由④知,FG为∠AFC的角平分线,
∴GH=GM,∴S△AGF:S△FGC=AF:FC,∵△AEF≌△AGF,△CDF≌△CGF,
∴S△AEF:S△FDC=AF:FC,故⑤正确.综上所述:正确的有①③④⑤,共4个,故选:C.
二、填空题
13.【解答】解:点M(3,﹣4)关于x轴的对称点M′的坐标是(3,4).故答案为:(3,4).
14. 【解答】解:∵∠APC=∠A+∠E,∠BOP=∠D+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F=∠B+∠C+∠APC+∠BOP=360°.故答案为:360°.
15.【解答】解:∵△ADE≌△BDE,∴,AE=BE,∵△ABC的周长比△AEC的周长大6,∴(AB+AC+BC)﹣(AE+EC+AC)=6,∴AB+BC﹣AE﹣EC=6,
∴AB+BE﹣AE=6,∴AB=6,∴,
故答案为:3.
16. AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD(答案不唯一) .(写出一个即可)
17.【解答】解:∵∠BAC=45°,CE⊥AB,∴CE=AE=7,
∵∠BCE+∠CHD=90°,∠EAH+∠AHE=90°,∠AHE=∠CHD,
∴∠BCE=∠EAH,在△BCE和△HAE中,
,∴△BCE≌△HAE(ASA),∴BE=EH,
∵BE+AE=AB=12,∴BE=EH=5,∴CH=CE﹣HE=7﹣5=2,故答案为:2.
18. 【解答】解:∵AD为中线,∴BD=CD.∵BE⊥AD,CF⊥AD,∴∠E=∠CFD=90°,
∵∠BDE=∠CDF,∴△BDE≌△CDF(AAS),∴BE=CF,DE=DF,故①正确;
∵∠G=∠BAD,∴△ABE≌△GCF(AAS),∴AE=GF,∴AG=EF,∴AG=2DE,故②正确;
∵BE=CF,∴S△AGC=2S△BDE,故④正确;
∴S△ABD=S△ACD,∴S△ABD+S△CDF=S△ACD+S△CDF=S△ACF+S△CDF+S△CDF=S△ACF+2S△CDF
=S△ACF+S△AGC=S△GCF,故③正确.故答案为:①②③④.
三、解答题
19【解答】解:(1)A(0,3),C(﹣2,1);
故答案为:(0,3);(﹣2,1);
(2)如图所示,△A1B1C1即为所求;
点B1(﹣4,﹣4);故答案为:(﹣4,﹣4);
(3)△A1B1C1的面积=.
20.【解答】解:设这个多边形是n边形,由题意得:
(n﹣2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
21. 【解答】解:(1)∵a,b,c是△ABC的三边,a=6,b=8,
∴2<c<14,
∵三角形的周长是小于22的偶数,
∴2<c<8,
∴c=4或6;
(2)|a+b﹣c|+|c﹣a﹣b|
=a+b﹣c﹣c+a+b
=2a+2b﹣2c.
22. 【解答】解:(1)∵AD平分∠BAC,∠BAC=68°,
∴.
∵∠ADB是△ADC的外角,∠C=52°,
∴∠ADB=∠C+∠DAC=86°;
(2)∵AD平分∠BAC,BE平分∠ABC,
∴∠BAC=2∠BAD,∠ABC=2∠ABE.
∵∠BED是△ABE的外角,∠BED=57°,
∴∠BAD+∠ABE=∠BED=57°,
∴∠BAC+∠ABC=2(∠BAD+∠ABE)=114°,
∵∠BAC+∠ABC+∠C=180°,
∴∠C=180°﹣(∠BAC+∠ABC)=66°.
23.【解答】解:(1)∵△ADC≌△AFB,
∴∠DAC=∠FAB.
∴∠DAC﹣∠BAC=∠FAB﹣∠BAC.
∴∠FAC=∠DAB=20°;
(2)∵DA∥BF,
∴∠DAF+∠F=180°.
∵△ADC≌△AFB,
∴∠D=∠F.
∴∠DAF+∠D=180°.
∴AF∥DC.
(3)∵AF∥DC,
∴∠F=∠FEC=110°.
∵AD∥BF,
∴∠DAF+∠F=180°.
∴∠DAF=180°﹣110°=70°.
∠BAC=∠DAF﹣∠FAC﹣∠DAB=70°﹣20°﹣20°=30°.
24. 【解答】(1)证明:在△ABC和△DBE中,BA=DB,BE=BC,AC=DE,
,
∴△ABC≌△DBE(SSS)
(2)解:在△ABC和△DBC中,
,
∴△ABC≌△DBC(SSS),
∴∠ACB=∠DCB,
∵∠ACD=72°=∠ACB+∠DCB,
∴,
∵△ABC≌△DBE,
∴∠BED=∠BCA=36°.
25. 【解答】解:(1)∵△ABC的两条高AD与BE交于点O,
∴∠BDO=∠ADC=∠AEB=90°,
∴∠DAC+∠AOE=90°,∠DBO+∠BOD=90°,
又∵∠AOE=∠BOD,
∴∠DAC=∠DBO=20°;
(2)在△ADC和△BDO中,
∠DAC=∠DBO,AD=BD,∠BDO=∠ADC=90°,
∴△ADC≌△BDO(ASA),
∴BO=AC=6;
(3)∵∠AOP=90°+∠DAC,∠ACM=∠BCN=90°+∠DAC,
∴∠AOP=∠ACM=∠BCN,
依题意得:OP=t,AQ=4t,
∵F是射线BC上一点,且CF=AO,
∴有以下两种情况:
①当点F在线段BC上时,
∵∠AOP=∠BCN,
∴当△AOP与△FCQ全等时,点Q在AC的延长线上,如图1所示:
此时OP=CQ,
∵AC=6,AQ=4t,
∴CQ=4t﹣6,
∴t=4t﹣6,
解得:t=2,
②当点F在BC的延长线上时,
∵∠AOP=∠ACM,
∴当△AOP与△FCQ全等时,点Q在线段AC上,如图2所示:
此时OP=CQ,
∵AC=6,AQ=4t,
∴CQ=6﹣4t,
∴t=6﹣4t,
解得:t=1.2,
综上所述:当△AOP与△FCQ全等时,t的值为2或1.2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年八年级(上)期中数学试卷模拟1
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列会徽中,不是轴对称图形的是( )
A. B. C. D.
2.一个多边形的每一个内角都是135°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.下列说法正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等三角形一定关于某条直线对称
C.两图形关于某条直线对称,则这两个图形一定分别位于对称轴的两侧
D.有一条公共边的两个全等三角形关于公共边的所在的直线对称
4.如图,已知∠1+2+∠3+∠4=280°,那么∠5的度数为( )
A.70° B.80° C.90° D.100°
5.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
6.一个多边形的内角和是外角和的四倍,它是几边形?( )
A.四 B.六 C.八 D.十
7.如图,△ABC中AC边上的高是( )
A.线段AE B.线段CB C.线段BE D.线段AB
8.下列长度的三条线段,能组成三角形的是( )
A.3,4,5 B.2,5,8 C.5,5,10 D.1,6,7
9.如图,∠A=42°,∠1=∠2,∠3=∠4,则∠M+∠N+∠P=( )
A.126° B.222° C.201° D.162°
10.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,连接AO,过点O作OD⊥BC,OE⊥AB,△ABC的面积是16,周长是8,则OD的长是( )
A.1 B.2 C.3 D.4
11.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
12.如图,在△ABC中,∠ABC=60°,AD平分∠BAC交BC于点D,CE平分∠ACB交AB于点E,AD、CE交于点F.则下列说法正确的个数为( )
①∠AFC=120°;②S△ABD=S△ADC,③若AB=2AE,则CE⊥AB;④CD+AE=AC;⑤S△AEF:S△FDC=AF:FC.
A.2个 B.3个 C.4个 D.5个
二、填空题:(本大题共6小题,每小题3分,共18分.)
13.点M(3,﹣4)关于x轴的对称点的坐标是 .
14.如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
15.如图,在△ABC中,点D,E分别在边AB和BC上,△ADE≌△BDE,且△ABC的周长比△AEC的周长大6,则AD的长为 .
16.如图,AB⊥BC,AD⊥DC,垂足分别为B,D.只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
17.如图,在△ABC中,∠BAC=45°,高AD,CE交于点H.若AB=12,CE=7,则CH= .
18.如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连接GC,使∠G=∠BAD.下列结论中正确的有 .(写序号)
①BE=CF;②AG=2DE;③S△ABD+S△CDF=S△GCF;④S△AGC=2S△BDE.
三、解答题:(本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.)
19. C在直角坐标系内的位置如图所示:
(1)分别写出点A,C的坐标:A的坐标: ,C的坐标: ;
(2)请在这个坐标系内画出与△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标 ;
(3)求△A1B1C1的面积.
20个多边形的内角和是它的外角和的3倍,求这个多边形的边数.
21知△ABC的三边长是a,b,c.
(1)若a=6,b=8,且三角形的周长是小于22的偶数,求c的值;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
22,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E.
(1)若∠C=52°,∠BAC=68°,求∠ADB的度数;
(2)若∠BED=57°,求∠C的度数.
23图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC、BF交于E,∠FEC=110°.
(1)求∠FAC的度数;
(2)AF平行于DC吗?说明理由;
(3)求∠BAC的度数.
24. 两个三角形纸板△ABC和△DBE按如图所示的方式摆放,连接DC.已知BA=DB,BE=BC,AC=DE=DC.
(1)求证:△ABC≌△DBE;
(2)若∠ACD=72°,求∠BED的度数.
25.如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6.(1)若∠DBO=20°,则∠DAC= ;
(2)求BO的长;
(3)F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P、Q两点同时停止运动,设运动时间为t(秒),当△AOP与△FCQ全等时,直接写出t的值.
答案解析
一、选择题
答案解析
一、选择题
1.【解答】解:A、B、D中图形,都能找到一条直线,折叠后直线两旁的部分重合,所以是轴对称图形;C中图形,不能找到一条直线,折叠后直线两旁的部分重合,所以不是轴对称图形.故选:C.
2.【解答】解:多边形的边数是:n=360÷(180﹣135)=8.故选:B.
3.【解答】解:A、关于某直线对称的两个三角形是全等三角形,正确,符合题意;
B、全等三角形是关于某直线对称的错误,例如图一,错误,不符合题意;
C、两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧错误,例如图二:错误,不符合题意;
D、有一条公共边的两个全等三角形关于公共边所在的直线对称,错误,例如图三,不符合题意,
故选:A.
4.【解答】解:由题意得:∠1+2+∠3+∠4+∠5=360°,∵∠1+2+∠3+∠4=280°,
∴∠5=360°﹣280°=80°,故选:B.
5.【解答】解:做法中用到的三角形全等的判定方法是SSS
证明如下:由题意得,PN=PM,在△ONP和△OMP中,
,
∴△ONP≌△OMP(SSS)所以∠NOP=∠MOP故OP为∠AOB的平分线.故选:A.
6. 【解答】解:设这个多边形是n边形,则(n﹣2)×180°=4×360°,整理得:n﹣2=8,
解得:n=10,即这个多边形是十边形.故选:D.
7.【解答】解:△ABC中AC边上的高是线段BE.故选:C.
8.【解答】解:A、3+4>5,故能构成三角形,故此选项符合题意;
B、2+5<8,故不能构成三角形,故此选项不符合题意;
C、5+5=10,故不能构成三角形,故此选项不符合题意;
D、1+6=7,故不能构成三角形,故此选项不符合题意.故选:A.
9. 【解答】解:图1:∵在△ABC中,∠A=60°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣42°=138°,∵∠1=∠2,∠3=∠4,∴,,
∴∠2+∠4==69°,∴∠M=180°﹣(∠2+∠4)=180°﹣69°=111°;
图2:∵∠ACD是△ABC的外角,∠A=42°,∴∠ACD=∠A+∠ABC,
∵∠1=∠2,∠3=∠4,∴2∠4=2∠2+∠A,∵∠NCD是△NBC的外角,
∴∠4=∠NCD=∠N+∠2,∴=21°;
图3:
∵∠DBC是△ABC的外角,∠ECB是△ABC的外角,∠A=42°,
∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC
=∠A+(∠ACB+∠A+∠ABC)=42°+180°=222°,
又∵∠1=∠2,∠3=∠4,∴,,
∴∠2+∠3==111°,∴∠P=180°﹣(∠2+∠3)=180°﹣111°=69°,
∴∠M+∠N+∠P=111°+21°+69°=201°.
故选:C.
10.【解答】解:如图,过点O作OF⊥AC于F,∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OD=OE,
∵OC平分∠ACB,OD⊥BC,OF⊥AC,∴OD=OF,∴OD=OE=OF,
由题意得:AB OE+BC OD+AC OF=16,∴×8×OD=16,解得:OD=4,
故选:D.
11. 【解答】解:①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;
②∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°,
∵△BAD≌△CAE,∴∠ABD=∠ACE,∴∠ACE+∠DBC=45°,本选项正确;
③∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,本选项正确;
④∵∠BAC=∠DAE=90°,∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故此选项正确,
故选:D.
12. 【解答】解:①在△ABC中,∠ABC=60°,∴∠ACB+∠CAB=120°,
∵AD平分∠BAC,CE平分∠ACB,∴∠FCA=,∠FAC=CAB,
∴∠AFC=180°﹣(∠FCA+∠FAC)=180°﹣(∠ACB+∠CAB)=120°,故①正确;
②当AD是△ABC的中线时,S△ABD=S△ADC,而AD平分∠BAC,故②错误;
③如图,延长CE至G,使GE=CE,连接BG,∵AB=2AE,∴AE=BE,∵∠AEC=∠BEG,
∴△ACE≌△BGE(SAS),∴∠ACE=∠G,CE=GE,∵CE为角平分线,∴∠ACE=∠BCE,
∴∠BCE=∠G,∴BC=BG,∵CE=GE,∴BE⊥CE,故③正确;
④如图,作∠AFC的平分线交AC于点G,
由①得∠AFC=120°,∴∠AFG=∠CFG=60°,∴∠AFE=60°,
∴∠AFG=∠CFG=∠AFE=60°,∵∠EAF=∠GAF,∠DCF=∠GCF,
∴△AEF≌△AGF(ASA),△CDF≌△CGF(ASA),∴AE=AG,CD=CG,
∴CD+AE=CG+AG=AC,故④正确;
⑤过G作GM⊥FC,GH⊥AF于点G,H,由④知,FG为∠AFC的角平分线,
∴GH=GM,∴S△AGF:S△FGC=AF:FC,∵△AEF≌△AGF,△CDF≌△CGF,
∴S△AEF:S△FDC=AF:FC,故⑤正确.综上所述:正确的有①③④⑤,共4个,故选:C.
二、填空题
13.【解答】解:点M(3,﹣4)关于x轴的对称点M′的坐标是(3,4).故答案为:(3,4).
14. 【解答】解:∵∠APC=∠A+∠E,∠BOP=∠D+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F=∠B+∠C+∠APC+∠BOP=360°.故答案为:360°.
15.【解答】解:∵△ADE≌△BDE,∴,AE=BE,∵△ABC的周长比△AEC的周长大6,∴(AB+AC+BC)﹣(AE+EC+AC)=6,∴AB+BC﹣AE﹣EC=6,
∴AB+BE﹣AE=6,∴AB=6,∴,
故答案为:3.
16. AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD(答案不唯一) .(写出一个即可)
17.【解答】解:∵∠BAC=45°,CE⊥AB,∴CE=AE=7,
∵∠BCE+∠CHD=90°,∠EAH+∠AHE=90°,∠AHE=∠CHD,
∴∠BCE=∠EAH,在△BCE和△HAE中,
,∴△BCE≌△HAE(ASA),∴BE=EH,
∵BE+AE=AB=12,∴BE=EH=5,∴CH=CE﹣HE=7﹣5=2,故答案为:2.
18. 【解答】解:∵AD为中线,∴BD=CD.∵BE⊥AD,CF⊥AD,∴∠E=∠CFD=90°,
∵∠BDE=∠CDF,∴△BDE≌△CDF(AAS),∴BE=CF,DE=DF,故①正确;
∵∠G=∠BAD,∴△ABE≌△GCF(AAS),∴AE=GF,∴AG=EF,∴AG=2DE,故②正确;
∵BE=CF,∴S△AGC=2S△BDE,故④正确;
∴S△ABD=S△ACD,∴S△ABD+S△CDF=S△ACD+S△CDF=S△ACF+S△CDF+S△CDF=S△ACF+2S△CDF
=S△ACF+S△AGC=S△GCF,故③正确.故答案为:①②③④.
三、解答题
19【解答】解:(1)A(0,3),C(﹣2,1);
故答案为:(0,3);(﹣2,1);
(2)如图所示,△A1B1C1即为所求;
点B1(﹣4,﹣4);故答案为:(﹣4,﹣4);
(3)△A1B1C1的面积=.
20.【解答】解:设这个多边形是n边形,由题意得:
(n﹣2)×180°=360°×3,
解得:n=8.
答:这个多边形的边数是8.
21. 【解答】解:(1)∵a,b,c是△ABC的三边,a=6,b=8,
∴2<c<14,
∵三角形的周长是小于22的偶数,
∴2<c<8,
∴c=4或6;
(2)|a+b﹣c|+|c﹣a﹣b|
=a+b﹣c﹣c+a+b
=2a+2b﹣2c.
22. 【解答】解:(1)∵AD平分∠BAC,∠BAC=68°,
∴.
∵∠ADB是△ADC的外角,∠C=52°,
∴∠ADB=∠C+∠DAC=86°;
(2)∵AD平分∠BAC,BE平分∠ABC,
∴∠BAC=2∠BAD,∠ABC=2∠ABE.
∵∠BED是△ABE的外角,∠BED=57°,
∴∠BAD+∠ABE=∠BED=57°,
∴∠BAC+∠ABC=2(∠BAD+∠ABE)=114°,
∵∠BAC+∠ABC+∠C=180°,
∴∠C=180°﹣(∠BAC+∠ABC)=66°.
23.【解答】解:(1)∵△ADC≌△AFB,
∴∠DAC=∠FAB.
∴∠DAC﹣∠BAC=∠FAB﹣∠BAC.
∴∠FAC=∠DAB=20°;
(2)∵DA∥BF,
∴∠DAF+∠F=180°.
∵△ADC≌△AFB,
∴∠D=∠F.
∴∠DAF+∠D=180°.
∴AF∥DC.
(3)∵AF∥DC,
∴∠F=∠FEC=110°.
∵AD∥BF,
∴∠DAF+∠F=180°.
∴∠DAF=180°﹣110°=70°.
∠BAC=∠DAF﹣∠FAC﹣∠DAB=70°﹣20°﹣20°=30°.
24. 【解答】(1)证明:在△ABC和△DBE中,BA=DB,BE=BC,AC=DE,
,
∴△ABC≌△DBE(SSS)
(2)解:在△ABC和△DBC中,
,
∴△ABC≌△DBC(SSS),
∴∠ACB=∠DCB,
∵∠ACD=72°=∠ACB+∠DCB,
∴,
∵△ABC≌△DBE,
∴∠BED=∠BCA=36°.
25. 【解答】解:(1)∵△ABC的两条高AD与BE交于点O,
∴∠BDO=∠ADC=∠AEB=90°,
∴∠DAC+∠AOE=90°,∠DBO+∠BOD=90°,
又∵∠AOE=∠BOD,
∴∠DAC=∠DBO=20°;
(2)在△ADC和△BDO中,
∠DAC=∠DBO,AD=BD,∠BDO=∠ADC=90°,
∴△ADC≌△BDO(ASA),
∴BO=AC=6;
(3)∵∠AOP=90°+∠DAC,∠ACM=∠BCN=90°+∠DAC,
∴∠AOP=∠ACM=∠BCN,
依题意得:OP=t,AQ=4t,
∵F是射线BC上一点,且CF=AO,
∴有以下两种情况:
①当点F在线段BC上时,
∵∠AOP=∠BCN,
∴当△AOP与△FCQ全等时,点Q在AC的延长线上,如图1所示:
此时OP=CQ,
∵AC=6,AQ=4t,
∴CQ=4t﹣6,
∴t=4t﹣6,
解得:t=2,
②当点F在BC的延长线上时,
∵∠AOP=∠ACM,
∴当△AOP与△FCQ全等时,点Q在线段AC上,如图2所示:
此时OP=CQ,
∵AC=6,AQ=4t,
∴CQ=6﹣4t,
∴t=6﹣4t,
解得:t=1.2,
综上所述:当△AOP与△FCQ全等时,t的值为2或1.2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
