人教版:2024-2025 八年级数学期中试卷 2(含答案解析)
文档属性
| 名称 | 人教版:2024-2025 八年级数学期中试卷 2(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 795.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 08:43:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024-2025学年八年级(上)期中数学试卷模拟2
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点P(3,﹣5)关于y轴对称点的坐标是( )
A.(﹣3,﹣5) B.(﹣3,5) C.(3,﹣5) D.(3,5)
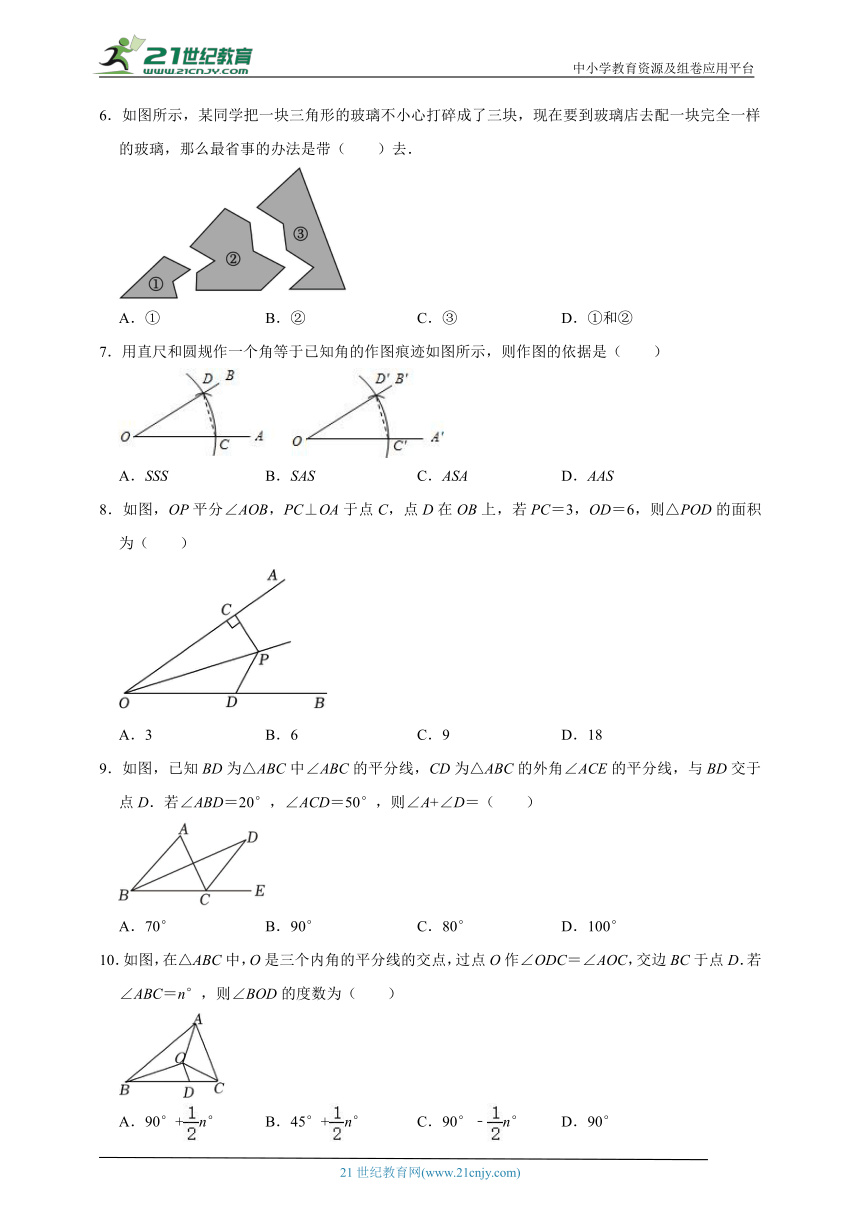
2.如图,已知BP是∠ABC的平分线,AP⊥BP,若△BPC的面积为8cm2,则△ABC的面积( )
A.18cm2 B.16cm2 C.12cm2 D.14cm2
3.下列说法正确的是( )
A.如果两个三角形全等,则它们必关于某条直线成轴对称
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形的对称轴是一条边上的中线所在的直线
D.所有的轴对称图形都只有一条对称轴
4.如图,点E,F在BC上,BF=CE,∠A=∠D.要使△ABF≌△DCE,需要添加下列选项中的
A.AF=DE B.AB=CD C.BE=CF D.∠B=∠C
5.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和37,则△EDF的面积为( )
A.11 B.5.5 C.6 D.3.5
6.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
7.用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
9.如图,已知BD为△ABC中∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,与BD交于点D.若∠ABD=20°,∠ACD=50°,则∠A+∠D=( )
A.70° B.90° C.80° D.100°
10.如图,在△ABC中,O是三个内角的平分线的交点,过点O作∠ODC=∠AOC,交边BC于点D.若∠ABC=n°,则∠BOD的度数为( )
A.90°+n° B.45°+n° C.90°﹣n° D.90°
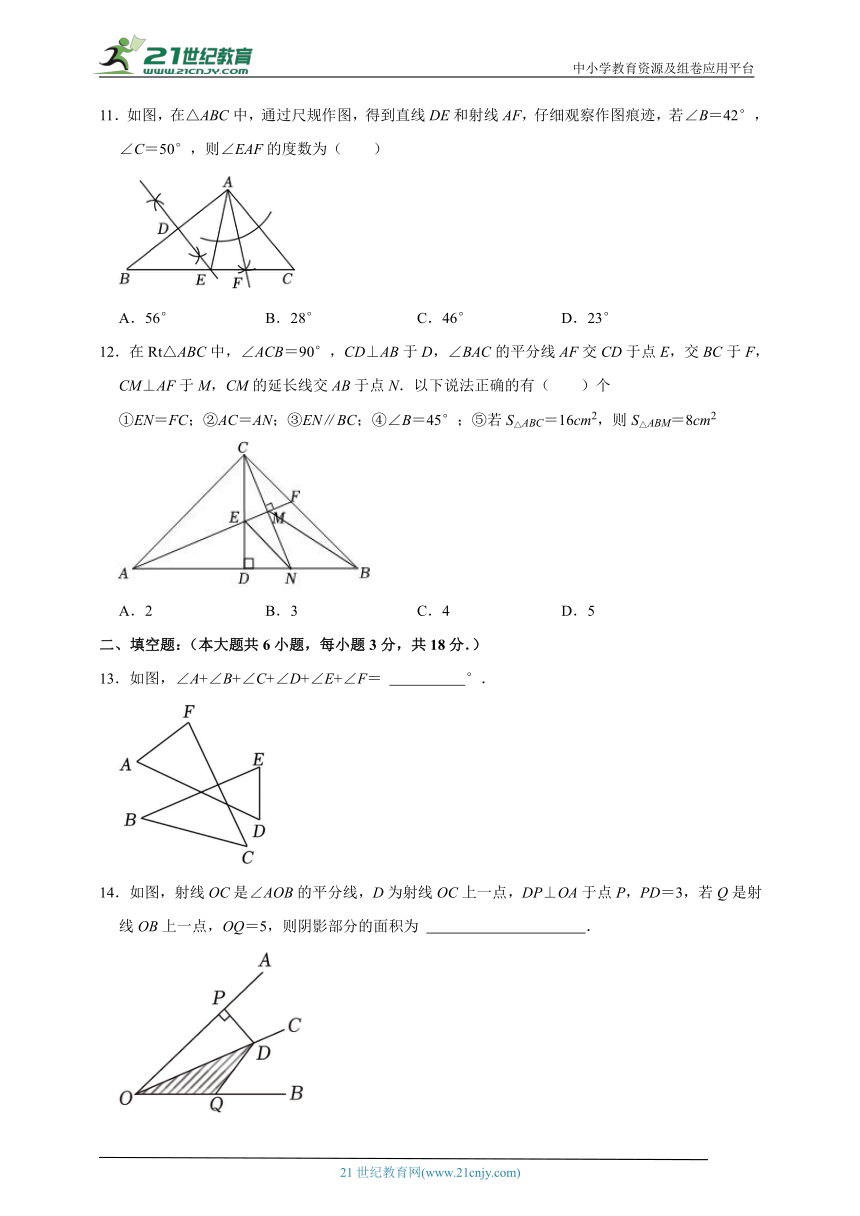
11.如图,在△ABC中,通过尺规作图,得到直线DE和射线AF,仔细观察作图痕迹,若∠B=42°,∠C=50°,则∠EAF的度数为( )
A.56° B.28° C.46° D.23°
12.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线AF交CD于点E,交BC于F,CM⊥AF于M,CM的延长线交AB于点N.以下说法正确的有( )个
①EN=FC;②AC=AN;③EN∥BC;④∠B=45°;⑤若S△ABC=16cm2,则S△ABM=8cm2
A.2 B.3 C.4 D.5
二、填空题:(本大题共6小题,每小题3分,共18分.)
13.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
14.如图,射线OC是∠AOB的平分线,D为射线OC上一点,DP⊥OA于点P,PD=3,若Q是射线OB上一点,OQ=5,则阴影部分的面积为 .
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE=52°,B、D、E在同一直线上,则∠BEC的度数为 .
16.如图,△ABC是等边三角形,D,E分别是AC,BC上的点,若AE=AD,∠CED=25°,则∠BAE= °.
17.如图所示,在△ABC中,AB=AC=10,DE垂直平分AB,△BDC的周长为18,则BC= .
18.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,当CF取最小值时,△BDE的周长为 .
三、解答题:(本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.)
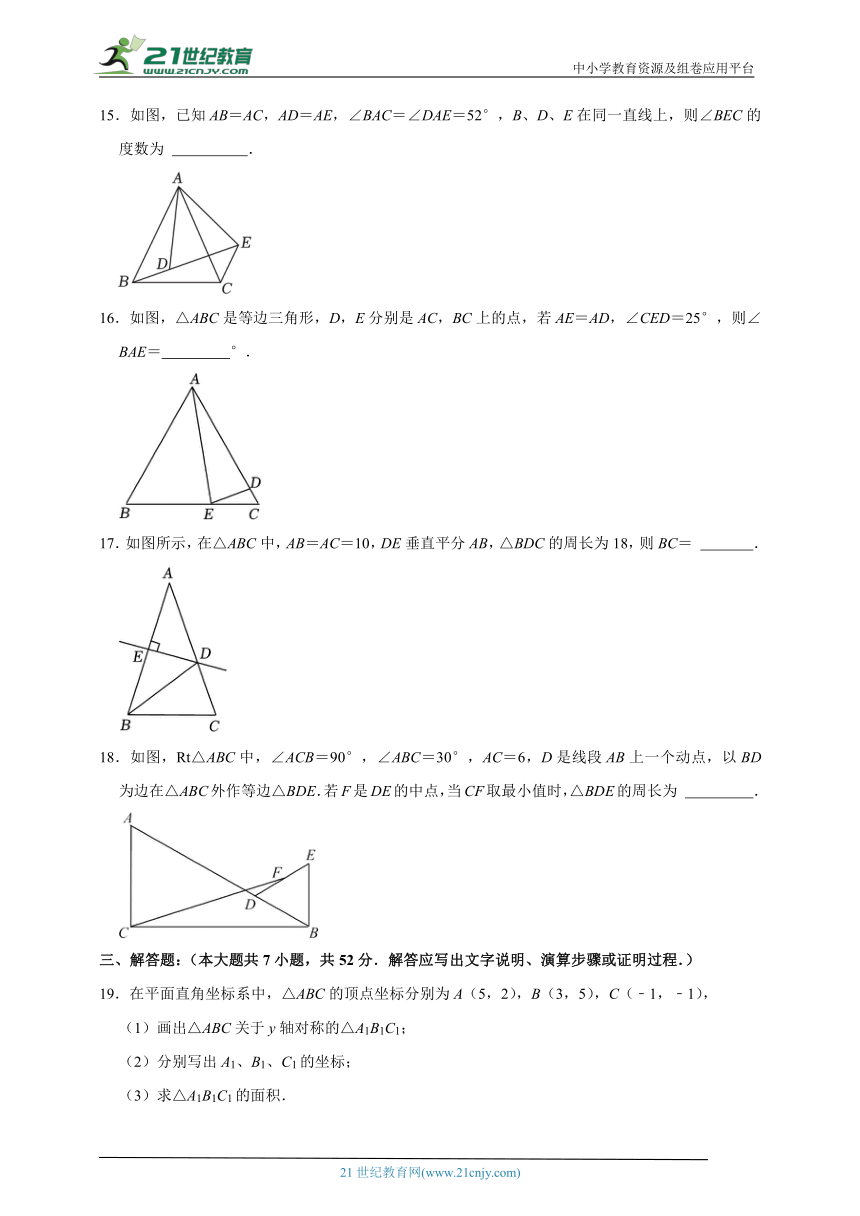
19.在平面直角坐标系中,△ABC的顶点坐标分别为A(5,2),B(3,5),C(﹣1,﹣1),
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)分别写出A1、B1、C1的坐标;
(3)求△A1B1C1的面积.
20.已知一个多边形的边数为n,若这个多边形的内角和的比一个七边形的外角和多72°,求n的值.
21.一个多边形除去一个内角后,其余内角之和是2570°,求:
(1)这个多边形的边数;
(2)除去的那个内角的度数.
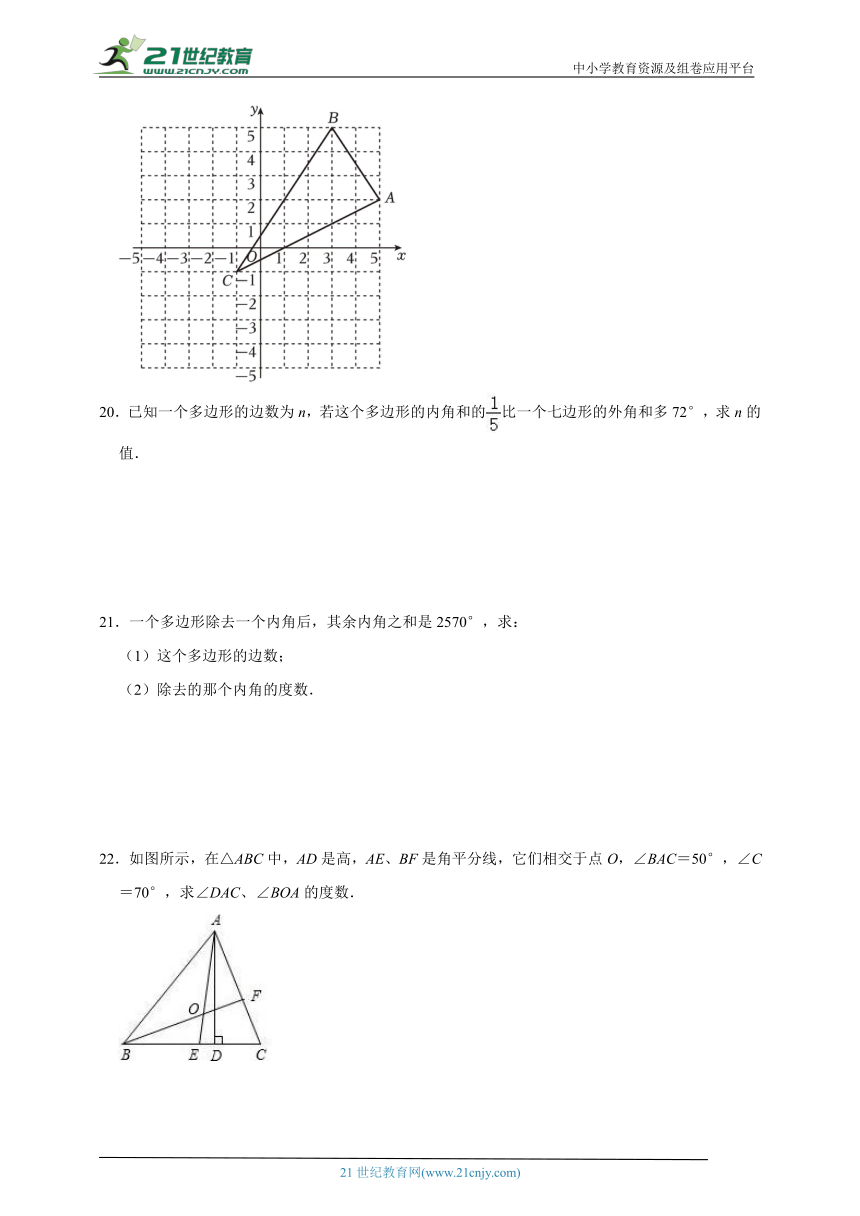
22.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.
23.如图,点B,C,D在同一条直线上,BC=DE,点A和点E在BD的同侧,∠ACE=∠B=∠D=60°.
(1)求证:△ABC≌△CDE;
(2)若DE=3,AB=4,求BD的长.
24.如图,已知AB=AC,AD=AE,∠BAC=∠EAD,∠1=25°,∠2=30°.
(1)求证:△ABE≌△ACD;
(2)求∠3的度数.
25.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图1),△ABD不动.
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图2),证明:MB=MC.
(2)若将图1中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图3),判断并直接写出MB、MC的数量关系.
(3)在(2)中,若∠CAE的大小改变(图4),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.
答案解析
选择题
1.【解答】解:根据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,可得点P(3,﹣5)关于y轴对称点的坐标是(﹣3,﹣5),故选:A.
2. 【解答】解:延长AP交BC于Q,如图所示:
∵BP是∠ABC的平分线,AP⊥BP,∴∠ABP=∠QBP,∠BPA=∠BPQ=90°,
在△ABP和△QBP中,,∴△ABP≌△QBP(ASA),
∴AP=QP,S△ABP=S△QBP,∴S△ACP=S△QCP,∵△BPC的面积为8cm2,
∴S△ABP+S△ACP=S△QBP+S△QCP=S△BPC=8,∴S△ABC=S△ABP+S△ACP+S△BPC=16.
故选:B.
3. 【解答】解:A、两个三角形全等,它们不一定关于某条直线成轴对称,故本选项说法错误,不合题意;
B、如果两个三角形关于某条直线成轴对称,那么它们是全等三角形,说法正确,故本选项符合题意;
C、等腰三角形的对称轴是底边上的中线所在的直线,故本选项说法错误,不合题意;
D、等边三角形就有三条对称轴,故本选项说法错误,不合题意;
故选:B.
4.解答】解:∵BF=CE,∠A=∠D,
A.添加AF=DE,不能判定△ABF≌△DCE,此选项错误,不符合题意;
B.添加AB=CD,不能判定△ABF≌△DCE,此选项错误,不符合题意;
C.添加BE=CF,不能判定△ABF≌△DCE,此选项错误,不符合题意;
D.添加∠B=∠C,根据AAS能判定△ABF≌△DCE,此选项正确,符合题意;
故选:D.
5.【解答】解:如图,过点D作DH⊥AC于H,∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,在Rt△ADF和Rt△ADH中,,∴Rt△ADF≌Rt△ADH(HL),
∴SRt△ADF=SRt△ADH,在Rt△DEF和Rt△DGH中,
∴Rt△DEF≌Rt△DGH(HL),∴SRt△DEF=SRt△DGH,∵△ADG和△AED的面积分别为48和37,
∴37+SRt△DEF=48﹣SRt△DGH,∴SRt△DEF=5.5.故选:B.
6.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.故选:C.
7.【解答】解:由作法易得OD=O′D',OC=0′C',CD=C′D',那么△OCD≌△O′C′D′,可得∠A′O′B′=∠AOB,所以利用的条件为SSS.
故选:A.
8.【解答】解:过P点作PE⊥OB于E点,如图,∵OP平分∠AOB,PC⊥OA,PE⊥OB,
∴PE=PC=3,∴S△POD=×6×3=9.故选:C.
9.【解答】解:∵∠ABC的平分线与∠ACB的外角平分线交于D,∠ABD=20°,∠ACD=55°,
∴∠ABD=∠DBC=∠ABC=20°,∠ACD=∠DCE=∠ACE=50°,
∴∠ABC=40°,∠ACE=100°,
∴∠A=∠ACE﹣∠ABC=60°,∠D=∠DCE﹣∠DBC=50°﹣20°=30°,
∴∠A+∠D=90°,
故选:B.
10.【解答】解:∵∠ABC=n°,
∴∠BAC+∠BCA=180°﹣∠ABC=180°﹣n°,
∵O是三个内角的平分线的交点,
∴∠OBC=ABC=n°,∠OCA=BCA,∠OAC=BAC,
∴∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣n°)=90°﹣n°,
∴∠AOC=180°﹣(∠OAC+∠OCA)=180°﹣(90°﹣n°)=90°+n°,
∵∠ODC=∠AOC,
∴∠ODC=∠AOC=90°+n°,
∵∠ODC=∠OBC+∠BOD,∠OBC=n°,
∴∠BOD=90°,选D
11.【解答】解:由作图可知,DE为线段AB的垂直平分线,AF为∠EAC的平分线,
∴AE=BE,,
∴∠BAE=∠B=42°,
∵∠B+∠C+∠BAE+∠EAC=180°,∠C=50°,
∴∠EAC=180°﹣∠B﹣∠C﹣∠BAE=180°﹣42°﹣50°﹣42°=46°,
∴∠,
故选:D.
12.【解答】解:如图,连接FN,
∵CN⊥AF,∴∠AMC=∠AMN=90°,∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,在△AMN和△AMC中,,∴△AMN≌△AMC(ASA),
∴AC=AN,故②正确;
∵△AMN≌△AMC,∴CM=NM,∵∠ACB=90°,CD⊥AB,∴∠ADC=90°,
∴∠AED+∠DAE=90°,∠CFE+∠CAE=90°,∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,∴∠AED=∠CFE,又∵∠AED=∠CEF,∴∠CEF=∠CFE,
∴CE=CF,∵CM⊥AF,∴EM=FM,∴四边形ENFC是菱形,
∴EN=FC,EN∥BC,故①③正确;
在Rt△ABC中,∠ACB=90°,∵AC≠BC,∴∠B≠45°,故④错误;
∵四边形ENFC是菱形,∴CM=MN,∴S△ACM=S△ANM,S△BCM=S△BMN,
∴S△ANM+S△BMN=S△ACM+S△BCM=S△ABC,∴S△ABM=S△ABC,
∴S△ABC=16cm2,则S△ABM=8cm2.故⑤正确.
综上所述:①②③⑤,共4个.故选C.
二、填空题
13.【解答】解:∵∠B+∠C=∠EGH,∠A+∠F=∠DHG,∠EGH+∠DHG+∠E+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,故答案为:360.
14.【解答】解:如图,过点D作DE⊥OB于E,
∵射线OC是∠AOB的平分线,D为射线OC上一点,DP⊥OA于点P,PD=3,
∴DE=PD=3,∵OQ=5,∴.故答案为:.
15.【解答】解:∵∠BAC=∠DAE=52°,∴∠BAD=∠CAE,在△ABD和△ACE中,
,∴△ABD≌△ACE((SAS),∴∠AEC=∠ADB,
∵∠ADB=∠AED+∠DAE,∴∠AEC=∠AED+∠DAE=∠AED+∠BEC,
∴∠BEC=∠DAE=52°,故答案为:52°.
16.【解答】解:∵△ABC是等边三角形,∴∠C=∠BAC=60°,
∵∠CED=25°,∴∠ADE=∠CED+∠C=85°,∵AE=AD,
∴∠AED=∠ADE=85°,∴∠DAE=180°﹣∠AED﹣∠ADE=10°,
∴∠BAE=∠BAC﹣∠DAE=60°﹣10°=50°,故答案为:50.
17.【解答】解:∵DE垂直平分AB,∴AD=BD,∴AC=AD+CD=BD+CD,
∵△BDC的周长=BC+CD+BD=BC+AC=18,∵AC=10,∴BC=8.故答案为:8.
18.【解答】解:连接BF,过点C作CH⊥BF.交BF的延长线于H,
∵△BDE是等边三角形,点F是DE的中点,∴∠ABF=30°,
∴点F在射线BF上运动,当点F与点H重合时,CF最小,
∵∠ACB=90°,∠ABC=30°,∴∠A=60°,AB=2AC=12,
∵∠ABF=30°,∴∠BD'H=∠AD'C=60°,
∴△ACD'是等边三角形,∴AD'=AC=6,
∴BD'=AB﹣AD'=12﹣6=6,∴△BDE的周长为:18,故答案为:18.
三、解答题
19【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,A1(﹣5,2),B1(﹣3,5),C1(1,﹣1).
(3)△A1B1C1的面积为=24﹣9﹣3=12.
20.【解答】解:依题意得,,
解得,n=14,
∴n的值为14.
21.【解答】解:(1)设这个多边形的边数为n,则其内角和为(n﹣2) 180°.
依题意,得2570°<(n﹣2) 180°<2 570°+180°,
解这个不等式组,得16<n<17.
因为n≥3,且n是整数,
所以n=17,即这个多边形的边数为17.
(2)除去的那个内角的度数为:(17﹣2) 180°﹣2570°=130°.
22.【解答】解:∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°.
23.【解答】(1)证明:∵B+∠A=∠ACE+∠DCE,∠ACE=∠B,
∴∠A=∠DCE,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS);
(2)解:∵△ABC≌△CDE,
∴AB=CD=4,
∵BC=DE=3,
∴BD=BC+CD=3+4=7.
24.【解答】(1)证明:∵BAC=∠BAE+∠CAE,∠DAE=∠1+∠CAE,∠BAC=∠DAE,
∴∠1=∠BAE,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS);
(2)解:∵△ABE≌△ACD,
∴∠2=∠ABD=30°,
∴∠3=∠BAE+∠ABD=∠1+∠ABD=25°+30°=55°.
25.【解答】证明:(1)如图2,连接AM,由已知得△ABD≌△ACE,
∴AD=AE,AB=AC,∠BAD=∠CAE,
∵MD=ME,
∴∠MAD=∠MAE,
∴∠MAD﹣∠BAD=∠MAE﹣∠CAE,
即∠BAM=∠CAM,
在△ABM和△ACM中,,
∴△ABM≌△ACM(SAS),
∴MB=MC;
(2)MB=MC.
理由如下:如图3,延长DB、AE相交于E′,延长EC交AD于F,
∴BD=BE′,CE=CF,
∵M是ED的中点,B是DE′的中点,
∴MB∥AE′,
∴∠MBC=∠CAE,
同理:MC∥AD,
∴∠BCM=∠BAD,
∵∠BAD=∠CAE,
∴∠MBC=∠BCM,
∴MB=MC;
解法二:如图3中,延长CM交BD于点T.
∵EC∥DT,∴∠CEM=∠TDM,在△ECM和△DTM中,
,∴△ECM≌△DTM(ASA),∴CM=MT,∵∠CBT=90°,∴BM=CM=MT.
(3)MB=MC还成立.
如图4,延长BM交CE于F,∵CE∥BD,
∴∠MDB=∠MEF,∠MBD=∠MFE,又∵M是DE的中点,
∴MD=ME,在△MDB和△MEF中,
,
∴△MDB≌△MEF(AAS),
∴MB=MF,∵∠ACE=90°,
∴∠BCF=90°,∴MB=MC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年八年级(上)期中数学试卷模拟2
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点P(3,﹣5)关于y轴对称点的坐标是( )
A.(﹣3,﹣5) B.(﹣3,5) C.(3,﹣5) D.(3,5)
2.如图,已知BP是∠ABC的平分线,AP⊥BP,若△BPC的面积为8cm2,则△ABC的面积( )
A.18cm2 B.16cm2 C.12cm2 D.14cm2
3.下列说法正确的是( )
A.如果两个三角形全等,则它们必关于某条直线成轴对称
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形的对称轴是一条边上的中线所在的直线
D.所有的轴对称图形都只有一条对称轴
4.如图,点E,F在BC上,BF=CE,∠A=∠D.要使△ABF≌△DCE,需要添加下列选项中的
A.AF=DE B.AB=CD C.BE=CF D.∠B=∠C
5.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和37,则△EDF的面积为( )
A.11 B.5.5 C.6 D.3.5
6.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
7.用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
9.如图,已知BD为△ABC中∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,与BD交于点D.若∠ABD=20°,∠ACD=50°,则∠A+∠D=( )
A.70° B.90° C.80° D.100°
10.如图,在△ABC中,O是三个内角的平分线的交点,过点O作∠ODC=∠AOC,交边BC于点D.若∠ABC=n°,则∠BOD的度数为( )
A.90°+n° B.45°+n° C.90°﹣n° D.90°
11.如图,在△ABC中,通过尺规作图,得到直线DE和射线AF,仔细观察作图痕迹,若∠B=42°,∠C=50°,则∠EAF的度数为( )
A.56° B.28° C.46° D.23°
12.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线AF交CD于点E,交BC于F,CM⊥AF于M,CM的延长线交AB于点N.以下说法正确的有( )个
①EN=FC;②AC=AN;③EN∥BC;④∠B=45°;⑤若S△ABC=16cm2,则S△ABM=8cm2
A.2 B.3 C.4 D.5
二、填空题:(本大题共6小题,每小题3分,共18分.)
13.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
14.如图,射线OC是∠AOB的平分线,D为射线OC上一点,DP⊥OA于点P,PD=3,若Q是射线OB上一点,OQ=5,则阴影部分的面积为 .
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE=52°,B、D、E在同一直线上,则∠BEC的度数为 .
16.如图,△ABC是等边三角形,D,E分别是AC,BC上的点,若AE=AD,∠CED=25°,则∠BAE= °.
17.如图所示,在△ABC中,AB=AC=10,DE垂直平分AB,△BDC的周长为18,则BC= .
18.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,当CF取最小值时,△BDE的周长为 .
三、解答题:(本大题共7小题,共52分.解答应写出文字说明、演算步骤或证明过程.)
19.在平面直角坐标系中,△ABC的顶点坐标分别为A(5,2),B(3,5),C(﹣1,﹣1),
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)分别写出A1、B1、C1的坐标;
(3)求△A1B1C1的面积.
20.已知一个多边形的边数为n,若这个多边形的内角和的比一个七边形的外角和多72°,求n的值.
21.一个多边形除去一个内角后,其余内角之和是2570°,求:
(1)这个多边形的边数;
(2)除去的那个内角的度数.
22.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.
23.如图,点B,C,D在同一条直线上,BC=DE,点A和点E在BD的同侧,∠ACE=∠B=∠D=60°.
(1)求证:△ABC≌△CDE;
(2)若DE=3,AB=4,求BD的长.
24.如图,已知AB=AC,AD=AE,∠BAC=∠EAD,∠1=25°,∠2=30°.
(1)求证:△ABE≌△ACD;
(2)求∠3的度数.
25.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图1),△ABD不动.
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图2),证明:MB=MC.
(2)若将图1中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图3),判断并直接写出MB、MC的数量关系.
(3)在(2)中,若∠CAE的大小改变(图4),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.
答案解析
选择题
1.【解答】解:根据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,可得点P(3,﹣5)关于y轴对称点的坐标是(﹣3,﹣5),故选:A.
2. 【解答】解:延长AP交BC于Q,如图所示:
∵BP是∠ABC的平分线,AP⊥BP,∴∠ABP=∠QBP,∠BPA=∠BPQ=90°,
在△ABP和△QBP中,,∴△ABP≌△QBP(ASA),
∴AP=QP,S△ABP=S△QBP,∴S△ACP=S△QCP,∵△BPC的面积为8cm2,
∴S△ABP+S△ACP=S△QBP+S△QCP=S△BPC=8,∴S△ABC=S△ABP+S△ACP+S△BPC=16.
故选:B.
3. 【解答】解:A、两个三角形全等,它们不一定关于某条直线成轴对称,故本选项说法错误,不合题意;
B、如果两个三角形关于某条直线成轴对称,那么它们是全等三角形,说法正确,故本选项符合题意;
C、等腰三角形的对称轴是底边上的中线所在的直线,故本选项说法错误,不合题意;
D、等边三角形就有三条对称轴,故本选项说法错误,不合题意;
故选:B.
4.解答】解:∵BF=CE,∠A=∠D,
A.添加AF=DE,不能判定△ABF≌△DCE,此选项错误,不符合题意;
B.添加AB=CD,不能判定△ABF≌△DCE,此选项错误,不符合题意;
C.添加BE=CF,不能判定△ABF≌△DCE,此选项错误,不符合题意;
D.添加∠B=∠C,根据AAS能判定△ABF≌△DCE,此选项正确,符合题意;
故选:D.
5.【解答】解:如图,过点D作DH⊥AC于H,∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,在Rt△ADF和Rt△ADH中,,∴Rt△ADF≌Rt△ADH(HL),
∴SRt△ADF=SRt△ADH,在Rt△DEF和Rt△DGH中,
∴Rt△DEF≌Rt△DGH(HL),∴SRt△DEF=SRt△DGH,∵△ADG和△AED的面积分别为48和37,
∴37+SRt△DEF=48﹣SRt△DGH,∴SRt△DEF=5.5.故选:B.
6.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.故选:C.
7.【解答】解:由作法易得OD=O′D',OC=0′C',CD=C′D',那么△OCD≌△O′C′D′,可得∠A′O′B′=∠AOB,所以利用的条件为SSS.
故选:A.
8.【解答】解:过P点作PE⊥OB于E点,如图,∵OP平分∠AOB,PC⊥OA,PE⊥OB,
∴PE=PC=3,∴S△POD=×6×3=9.故选:C.
9.【解答】解:∵∠ABC的平分线与∠ACB的外角平分线交于D,∠ABD=20°,∠ACD=55°,
∴∠ABD=∠DBC=∠ABC=20°,∠ACD=∠DCE=∠ACE=50°,
∴∠ABC=40°,∠ACE=100°,
∴∠A=∠ACE﹣∠ABC=60°,∠D=∠DCE﹣∠DBC=50°﹣20°=30°,
∴∠A+∠D=90°,
故选:B.
10.【解答】解:∵∠ABC=n°,
∴∠BAC+∠BCA=180°﹣∠ABC=180°﹣n°,
∵O是三个内角的平分线的交点,
∴∠OBC=ABC=n°,∠OCA=BCA,∠OAC=BAC,
∴∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣n°)=90°﹣n°,
∴∠AOC=180°﹣(∠OAC+∠OCA)=180°﹣(90°﹣n°)=90°+n°,
∵∠ODC=∠AOC,
∴∠ODC=∠AOC=90°+n°,
∵∠ODC=∠OBC+∠BOD,∠OBC=n°,
∴∠BOD=90°,选D
11.【解答】解:由作图可知,DE为线段AB的垂直平分线,AF为∠EAC的平分线,
∴AE=BE,,
∴∠BAE=∠B=42°,
∵∠B+∠C+∠BAE+∠EAC=180°,∠C=50°,
∴∠EAC=180°﹣∠B﹣∠C﹣∠BAE=180°﹣42°﹣50°﹣42°=46°,
∴∠,
故选:D.
12.【解答】解:如图,连接FN,
∵CN⊥AF,∴∠AMC=∠AMN=90°,∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,在△AMN和△AMC中,,∴△AMN≌△AMC(ASA),
∴AC=AN,故②正确;
∵△AMN≌△AMC,∴CM=NM,∵∠ACB=90°,CD⊥AB,∴∠ADC=90°,
∴∠AED+∠DAE=90°,∠CFE+∠CAE=90°,∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,∴∠AED=∠CFE,又∵∠AED=∠CEF,∴∠CEF=∠CFE,
∴CE=CF,∵CM⊥AF,∴EM=FM,∴四边形ENFC是菱形,
∴EN=FC,EN∥BC,故①③正确;
在Rt△ABC中,∠ACB=90°,∵AC≠BC,∴∠B≠45°,故④错误;
∵四边形ENFC是菱形,∴CM=MN,∴S△ACM=S△ANM,S△BCM=S△BMN,
∴S△ANM+S△BMN=S△ACM+S△BCM=S△ABC,∴S△ABM=S△ABC,
∴S△ABC=16cm2,则S△ABM=8cm2.故⑤正确.
综上所述:①②③⑤,共4个.故选C.
二、填空题
13.【解答】解:∵∠B+∠C=∠EGH,∠A+∠F=∠DHG,∠EGH+∠DHG+∠E+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,故答案为:360.
14.【解答】解:如图,过点D作DE⊥OB于E,
∵射线OC是∠AOB的平分线,D为射线OC上一点,DP⊥OA于点P,PD=3,
∴DE=PD=3,∵OQ=5,∴.故答案为:.
15.【解答】解:∵∠BAC=∠DAE=52°,∴∠BAD=∠CAE,在△ABD和△ACE中,
,∴△ABD≌△ACE((SAS),∴∠AEC=∠ADB,
∵∠ADB=∠AED+∠DAE,∴∠AEC=∠AED+∠DAE=∠AED+∠BEC,
∴∠BEC=∠DAE=52°,故答案为:52°.
16.【解答】解:∵△ABC是等边三角形,∴∠C=∠BAC=60°,
∵∠CED=25°,∴∠ADE=∠CED+∠C=85°,∵AE=AD,
∴∠AED=∠ADE=85°,∴∠DAE=180°﹣∠AED﹣∠ADE=10°,
∴∠BAE=∠BAC﹣∠DAE=60°﹣10°=50°,故答案为:50.
17.【解答】解:∵DE垂直平分AB,∴AD=BD,∴AC=AD+CD=BD+CD,
∵△BDC的周长=BC+CD+BD=BC+AC=18,∵AC=10,∴BC=8.故答案为:8.
18.【解答】解:连接BF,过点C作CH⊥BF.交BF的延长线于H,
∵△BDE是等边三角形,点F是DE的中点,∴∠ABF=30°,
∴点F在射线BF上运动,当点F与点H重合时,CF最小,
∵∠ACB=90°,∠ABC=30°,∴∠A=60°,AB=2AC=12,
∵∠ABF=30°,∴∠BD'H=∠AD'C=60°,
∴△ACD'是等边三角形,∴AD'=AC=6,
∴BD'=AB﹣AD'=12﹣6=6,∴△BDE的周长为:18,故答案为:18.
三、解答题
19【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,A1(﹣5,2),B1(﹣3,5),C1(1,﹣1).
(3)△A1B1C1的面积为=24﹣9﹣3=12.
20.【解答】解:依题意得,,
解得,n=14,
∴n的值为14.
21.【解答】解:(1)设这个多边形的边数为n,则其内角和为(n﹣2) 180°.
依题意,得2570°<(n﹣2) 180°<2 570°+180°,
解这个不等式组,得16<n<17.
因为n≥3,且n是整数,
所以n=17,即这个多边形的边数为17.
(2)除去的那个内角的度数为:(17﹣2) 180°﹣2570°=130°.
22.【解答】解:∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°.
23.【解答】(1)证明:∵B+∠A=∠ACE+∠DCE,∠ACE=∠B,
∴∠A=∠DCE,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS);
(2)解:∵△ABC≌△CDE,
∴AB=CD=4,
∵BC=DE=3,
∴BD=BC+CD=3+4=7.
24.【解答】(1)证明:∵BAC=∠BAE+∠CAE,∠DAE=∠1+∠CAE,∠BAC=∠DAE,
∴∠1=∠BAE,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS);
(2)解:∵△ABE≌△ACD,
∴∠2=∠ABD=30°,
∴∠3=∠BAE+∠ABD=∠1+∠ABD=25°+30°=55°.
25.【解答】证明:(1)如图2,连接AM,由已知得△ABD≌△ACE,
∴AD=AE,AB=AC,∠BAD=∠CAE,
∵MD=ME,
∴∠MAD=∠MAE,
∴∠MAD﹣∠BAD=∠MAE﹣∠CAE,
即∠BAM=∠CAM,
在△ABM和△ACM中,,
∴△ABM≌△ACM(SAS),
∴MB=MC;
(2)MB=MC.
理由如下:如图3,延长DB、AE相交于E′,延长EC交AD于F,
∴BD=BE′,CE=CF,
∵M是ED的中点,B是DE′的中点,
∴MB∥AE′,
∴∠MBC=∠CAE,
同理:MC∥AD,
∴∠BCM=∠BAD,
∵∠BAD=∠CAE,
∴∠MBC=∠BCM,
∴MB=MC;
解法二:如图3中,延长CM交BD于点T.
∵EC∥DT,∴∠CEM=∠TDM,在△ECM和△DTM中,
,∴△ECM≌△DTM(ASA),∴CM=MT,∵∠CBT=90°,∴BM=CM=MT.
(3)MB=MC还成立.
如图4,延长BM交CE于F,∵CE∥BD,
∴∠MDB=∠MEF,∠MBD=∠MFE,又∵M是DE的中点,
∴MD=ME,在△MDB和△MEF中,
,
∴△MDB≌△MEF(AAS),
∴MB=MF,∵∠ACE=90°,
∴∠BCF=90°,∴MB=MC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
