福建省安溪蓝溪中学高中数学人教版必修二2-2-1直线与平面平行的判定正课件(共20张PPT)
文档属性
| 名称 | 福建省安溪蓝溪中学高中数学人教版必修二2-2-1直线与平面平行的判定正课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-03 14:43:51 | ||
图片预览





文档简介
课件20张PPT。2.2.1直线与平面平行的判定蓝溪高中 易锰键 教学目标:
1、理解证明线面平行的判定定理。
即三个条件缺一不可
2、能熟练运用判定定理进行证明。包括:
(1)能比较熟练的书写证明 过程
(2)会用三角形中位线,平行四边形的平行关系来证明,
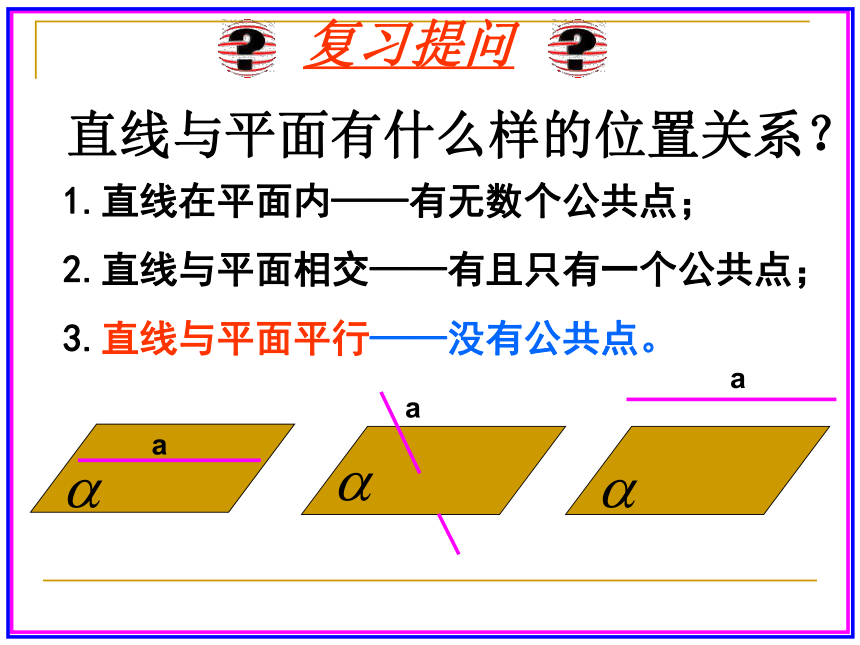
(3)会添加辅助线 复习提问直线与平面有什么样的位置关系?1.直线在平面内——有无数个公共点;
2.直线与平面相交——有且只有一个公共点;
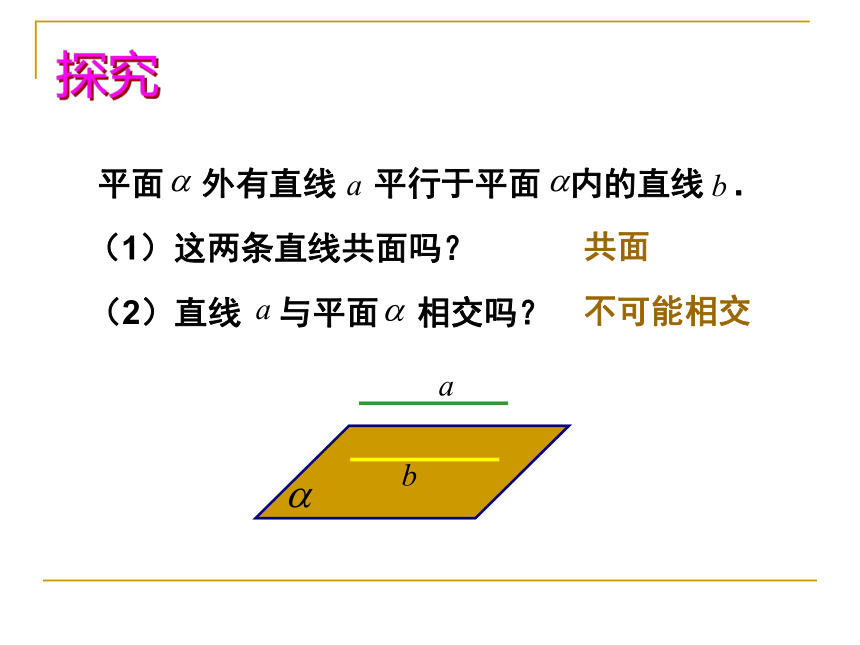
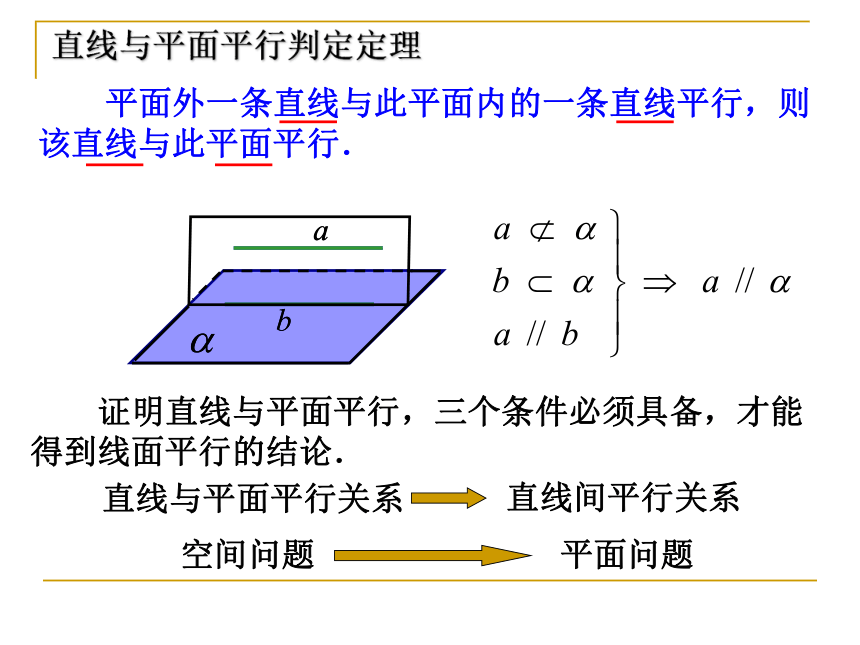
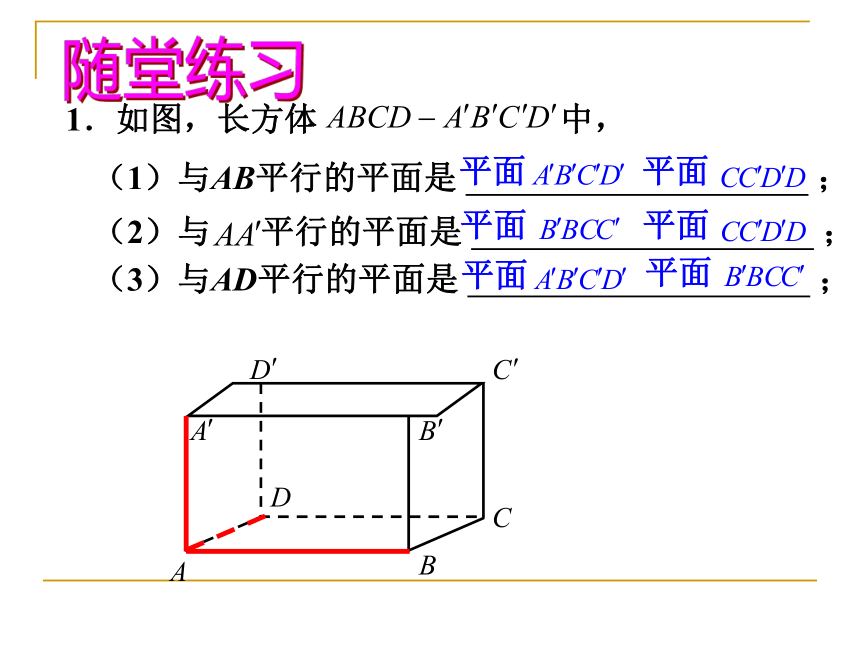
3.直线与平面平行——没有公共点。 怎样判定直线与平面平行呢?问题 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢?观察 将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?猜想(1)这两条直线共面吗?探究共面不可能相交 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.直线与平面平行判定定理 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;随堂练习定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?证明:连结BD.
∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质)ABDEF1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD变式1:ABCDEF变式2:ABCDFOE 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.(04年天津高考)分析:连结OF,可知OF为△ABE的中位线,所以得到AB//OF.∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,BDFO 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连结OF,ACE变式2: 分析:要证BD1//平面AEC即要在平面AEC内找一条直线与BD1平行.根据已知条件应该怎样考虑辅助线?巩固练习: 1.如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.O 证明:连结BD交AC于O,连结EO.
∵O 为矩形ABCD对角线的交点,
∴DO=OB,
又∵DE=ED1,
∴BD1//EO.
O巩固练习: 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.变式3:已知:如图,四棱锥P-ABCD中, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PAD分析:找一条在平面
PAD内并且和MN平行
的线O平行四边形的平行关系归纳小结,理清知识体系1.你认为判定直线与平面平行的需要注意几个条件?2.证明线面平行关键是什么?常用方法有哪些?
三角形的中位线、平行四边形的平行关系关键:找平行线1.如图,四棱锥P—ABCD中, 底面为正方形ABCD,O,E分别为BD、PC的中点. 求证:OE//平面PAD.作业:
1、理解证明线面平行的判定定理。
即三个条件缺一不可
2、能熟练运用判定定理进行证明。包括:
(1)能比较熟练的书写证明 过程
(2)会用三角形中位线,平行四边形的平行关系来证明,
(3)会添加辅助线 复习提问直线与平面有什么样的位置关系?1.直线在平面内——有无数个公共点;
2.直线与平面相交——有且只有一个公共点;
3.直线与平面平行——没有公共点。 怎样判定直线与平面平行呢?问题 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢?观察 将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?猜想(1)这两条直线共面吗?探究共面不可能相交 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.直线与平面平行判定定理 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;随堂练习定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?证明:连结BD.
∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质)ABDEF1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD变式1:ABCDEF变式2:ABCDFOE 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.(04年天津高考)分析:连结OF,可知OF为△ABE的中位线,所以得到AB//OF.∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,BDFO 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连结OF,ACE变式2: 分析:要证BD1//平面AEC即要在平面AEC内找一条直线与BD1平行.根据已知条件应该怎样考虑辅助线?巩固练习: 1.如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.O 证明:连结BD交AC于O,连结EO.
∵O 为矩形ABCD对角线的交点,
∴DO=OB,
又∵DE=ED1,
∴BD1//EO.
O巩固练习: 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.变式3:已知:如图,四棱锥P-ABCD中, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PAD分析:找一条在平面
PAD内并且和MN平行
的线O平行四边形的平行关系归纳小结,理清知识体系1.你认为判定直线与平面平行的需要注意几个条件?2.证明线面平行关键是什么?常用方法有哪些?
三角形的中位线、平行四边形的平行关系关键:找平行线1.如图,四棱锥P—ABCD中, 底面为正方形ABCD,O,E分别为BD、PC的中点. 求证:OE//平面PAD.作业:
