线性规划
图片预览


文档简介
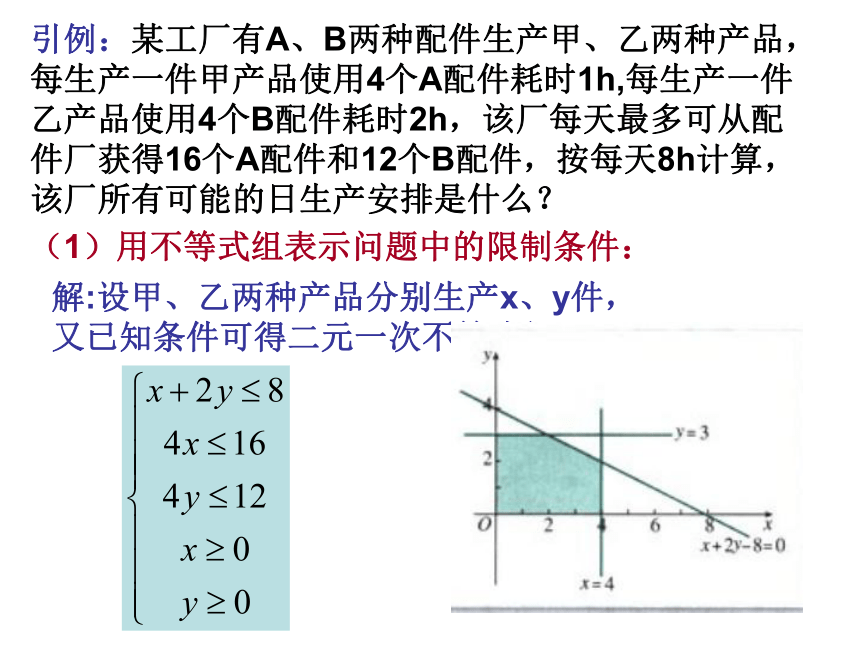
课件12张PPT。简单线性规划美国数学家,美国全国科学院院士。线性规划的奠基人。 1974年丹齐克在总结前人工作的基础上创立了线性规划,确定了这一学科的范围,并提出了解决线性规划问题的单纯形法 1937~1939年任美国劳工统计局统计员,1941~1952年任美国空军司令部数学顾问、战斗分析部和统计管理部主任丹齐克是美国运筹学会和国际运筹学会联合会 (IFORS)的主席和美国数学规划学会的创始人。他发表过100多篇关于数学规划及其应用方面的论文,1963年出版专著《线性规划及其范围》,这本著作至今仍是线性规划方面的标准参考书。 引例:某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,该厂所有可能的日生产安排是什么?解:设甲、乙两种产品分别生产x、y件,
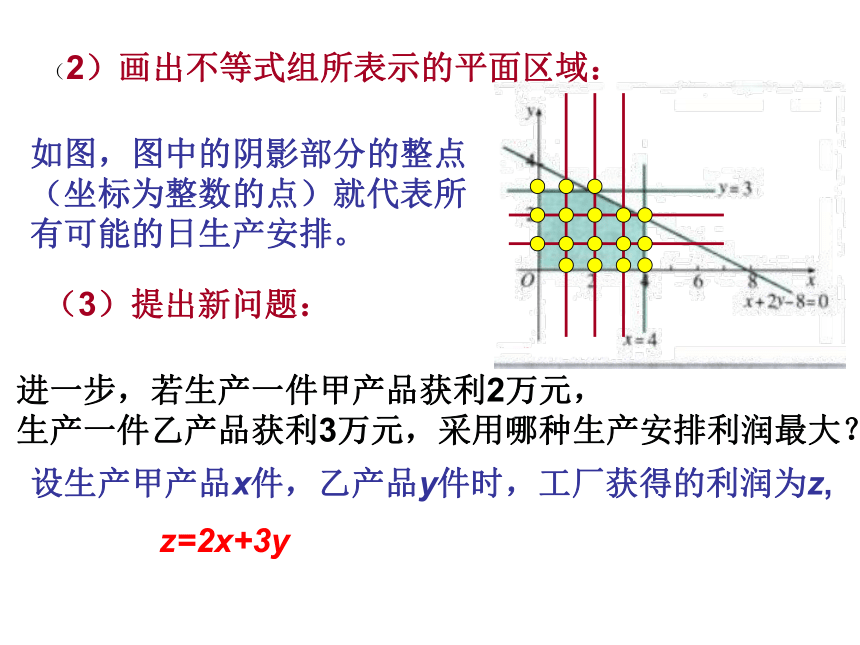
又已知条件可得二元一次不等式组:(1)用不等式组表示问题中的限制条件:(2)画出不等式组所表示的平面区域:如图,图中的阴影部分的整点
(坐标为整数的点)就代表所
有可能的日生产安排。(3)提出新问题:进一步,若生产一件甲产品获利2万元,
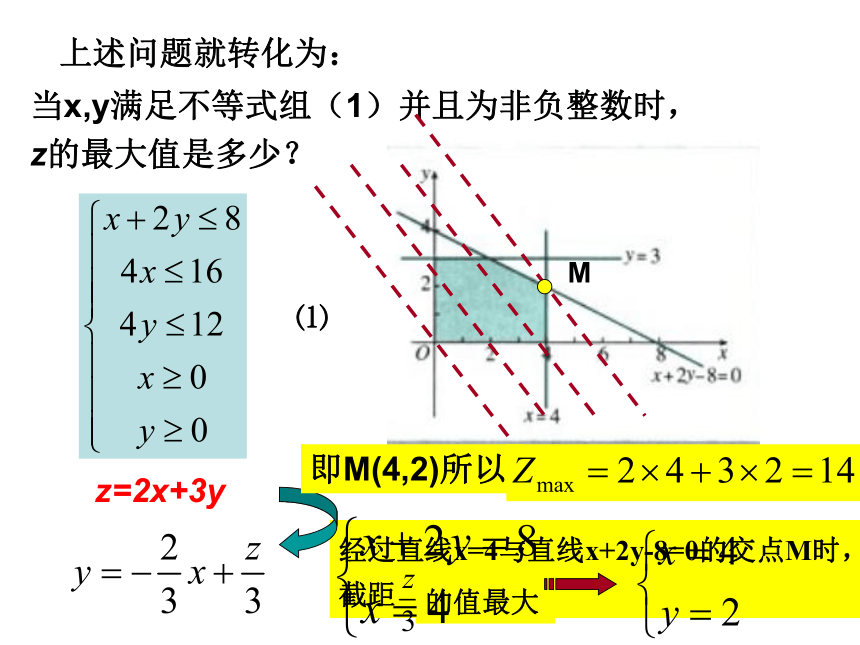
生产一件乙产品获利3万元,采用哪种生产安排利润最大?设生产甲产品x件,乙产品y件时,工厂获得的利润为z, z=2x+3y 当x,y满足不等式组(1)并且为非负整数时,
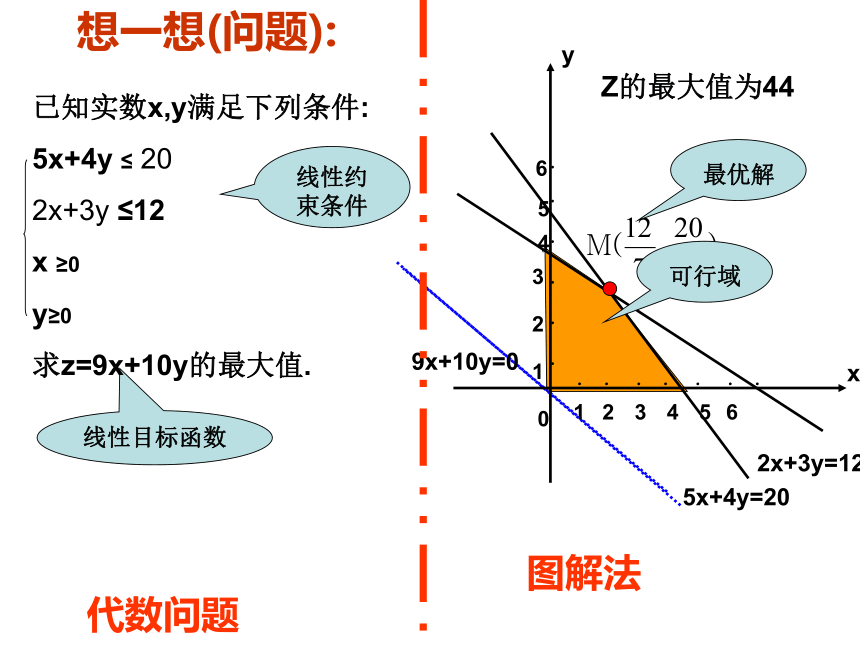
z的最大值是多少?上述问题就转化为: ⑴z=2x+3y即M(4,2)所以线性目标函数Z的最大值为44想一想(问题):线性约束条件代数问题图解法线性规划的有关概念: 线性规划:在线性约束条件下求线性目标函数的最大值或最小值的问题,统称为线性规划问题.可行域 :由所有可行解组成的集合叫做可行域;可行解 :满足线性约束条件的解(x,y)叫可行解;最优解 :使目标函数取得最大或最小值的可行解
叫线性规划问题的最优解。线性约束条件:不等式组是一组变量x、y的约束 条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.例5 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?将已知数据列表得解:设每天食用xkg食物A,ykg食物B,总成本为z,那么解:设每天食用xkg食物A,ykg食物B,总成本为z,那么目标函数为z=28x+21y作出二元一次不等式组所表示的可行域,如图:目标函数为z=28x+21y答:每天食用食物A约143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.用图解法解决简单的线性规划问题的基本步骤: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解四个步骤:1。画(画可行域)三个转化4。答(求出点的坐标,并转化为最优解)3。移(平移直线L 。寻找使纵截距取得最值时的点)2。作(作z=Ax+By=0时的直线L 。)图解法想一想(结论):线性约束条件可行域线性目标函数
Z=Ax+By最优解寻找平行线组的
最大(小)纵截距
又已知条件可得二元一次不等式组:(1)用不等式组表示问题中的限制条件:(2)画出不等式组所表示的平面区域:如图,图中的阴影部分的整点
(坐标为整数的点)就代表所
有可能的日生产安排。(3)提出新问题:进一步,若生产一件甲产品获利2万元,
生产一件乙产品获利3万元,采用哪种生产安排利润最大?设生产甲产品x件,乙产品y件时,工厂获得的利润为z, z=2x+3y 当x,y满足不等式组(1)并且为非负整数时,
z的最大值是多少?上述问题就转化为: ⑴z=2x+3y即M(4,2)所以线性目标函数Z的最大值为44想一想(问题):线性约束条件代数问题图解法线性规划的有关概念: 线性规划:在线性约束条件下求线性目标函数的最大值或最小值的问题,统称为线性规划问题.可行域 :由所有可行解组成的集合叫做可行域;可行解 :满足线性约束条件的解(x,y)叫可行解;最优解 :使目标函数取得最大或最小值的可行解
叫线性规划问题的最优解。线性约束条件:不等式组是一组变量x、y的约束 条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.例5 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?将已知数据列表得解:设每天食用xkg食物A,ykg食物B,总成本为z,那么解:设每天食用xkg食物A,ykg食物B,总成本为z,那么目标函数为z=28x+21y作出二元一次不等式组所表示的可行域,如图:目标函数为z=28x+21y答:每天食用食物A约143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.用图解法解决简单的线性规划问题的基本步骤: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解四个步骤:1。画(画可行域)三个转化4。答(求出点的坐标,并转化为最优解)3。移(平移直线L 。寻找使纵截距取得最值时的点)2。作(作z=Ax+By=0时的直线L 。)图解法想一想(结论):线性约束条件可行域线性目标函数
Z=Ax+By最优解寻找平行线组的
最大(小)纵截距
