福建省安溪蓝溪中学高中数学人教版必修二4-2-1直线与圆的位置关系1课件(共19张PPT)
文档属性
| 名称 | 福建省安溪蓝溪中学高中数学人教版必修二4-2-1直线与圆的位置关系1课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-03 14:59:47 | ||
图片预览





文档简介
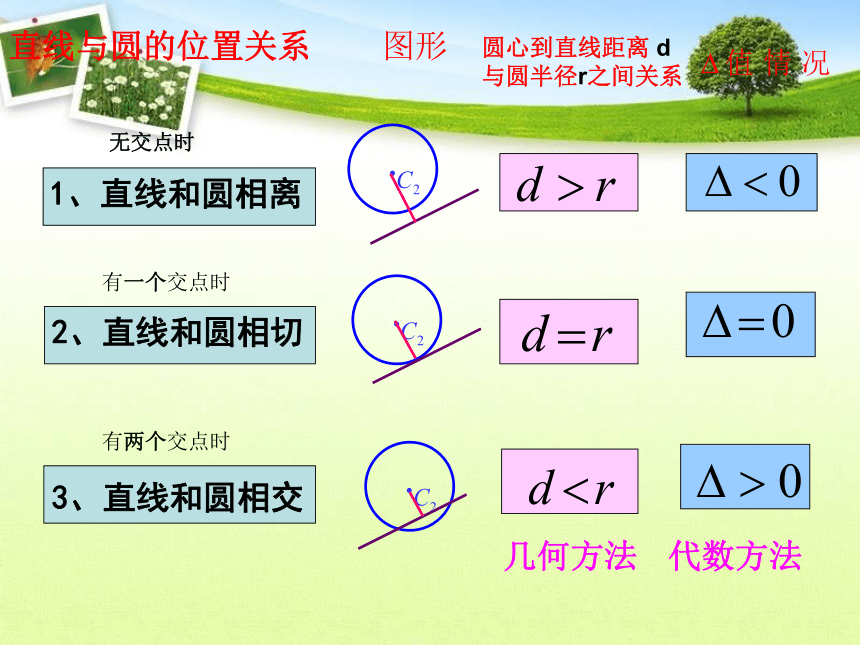
课件19张PPT。4.2.1 直线与圆的位置关系4.2 直线、圆的位置关系 第四章 圆与方程1、直线和圆相离2、直线和圆相切3、直线和圆相交直线与圆的位置关系图形圆心到直线距离 d 与圆半径r之间关系几何方法代数方法无交点时有一个交点时有两个交点时练习1.已知直线l:Ax+By+C=0,圆C:
(r>0),圆心C(a,b)到直线l的距离为d,若l与C相交,
则d__r, 若l与C相切,则d__r,若l与圆相离,则
d___r,2.圆心和弦的中点的连线 这条弦,圆心与
切点的连线____ 过该点的切线。 <>=垂直垂直。方程是的切线的圆,过圆上点的值为相切,则 与圆若直线____________51)-(y3)-(x1)-(24.) D (a 02x-yx01ya)x(1.32222=+=+=+++A 1或-1 B 2或-2 C 1 D -1X+2y=05、M(3,0)是圆x2+y2-8x-2y+10=0内一点,则过点M
最长的弦所在的直线方程是( )
A.. x+y-3=0 B. 2x-y-6=0
C. x-y-3=0 D. 2x+y-6=06、设点P(3,2)是圆(x-2)2+(y-1)2=4内部一点,则以P为
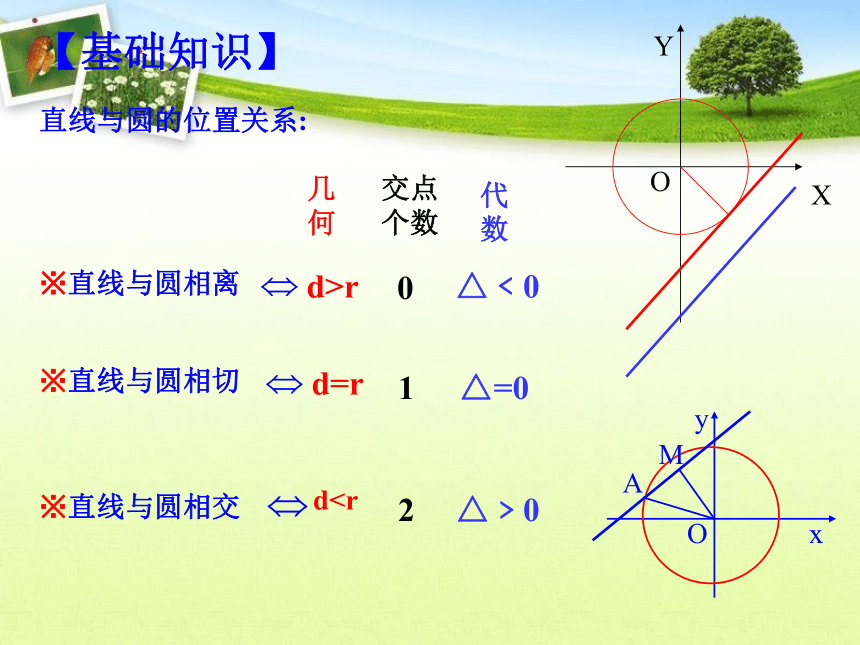
中点的弦所在的直线方程___________________.Cx+y-5=0【基础知识】直线与圆的位置关系:※直线与圆相离※直线与圆相切※直线与圆相交XYO几何 d>r交点个数0代数△﹤0 d=r1△=0 dA 相交 B相切 C相离 D与k值有关A相离典型例题1因此所证命题成立解法1:代 数 方 法圆的弦长ABl(2)由平面解析几何的垂径定理可知lAB解:(2)如图,有平面几何垂径定理知变式演练1解法2:(1)由圆方程可知,圆心为(0,1),半径为 r = 则 圆心到直线 l 的距离为 因此所证命题成立几何方法lAB解法3:mx-y+1-m=0过定点(1,1)而(1,1)在圆内,所以直线与圆相交。22例2: 在圆(x+1) +(y+2) =8上到直线x+y+1=0的距离为 的点有_____个.
3.pAB1.已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0当直线l
被C截得的弦长为 时,则a=( )
(A) (B) (C) (D) C.CLABD能力提升:2. 圆(x-3)2+(y+5)2=50被直线4x-3y=2截得
的弦长是________.能力提升103.直线 截圆x2+y2=4所得劣弧
所对圆心角大小为_______.圆心到直线距离 d=OABxy得∠AOB=2∠MOA=600能力提升能力提升Ax-y-3=0小结:1.圆的弦心距、半径、弦长的一半构成一个直角
三角形,在求圆的弦长时要利用到;2.求圆的切线方程时,一般是利用圆心到切线的
距离等于圆的半径。3.经过圆外一点作圆的切线有两条,特别要注意
是否有斜率不存在的直线
(r>0),圆心C(a,b)到直线l的距离为d,若l与C相交,
则d__r, 若l与C相切,则d__r,若l与圆相离,则
d___r,2.圆心和弦的中点的连线 这条弦,圆心与
切点的连线____ 过该点的切线。 <>=垂直垂直。方程是的切线的圆,过圆上点的值为相切,则 与圆若直线____________51)-(y3)-(x1)-(24.) D (a 02x-yx01ya)x(1.32222=+=+=+++A 1或-1 B 2或-2 C 1 D -1X+2y=05、M(3,0)是圆x2+y2-8x-2y+10=0内一点,则过点M
最长的弦所在的直线方程是( )
A.. x+y-3=0 B. 2x-y-6=0
C. x-y-3=0 D. 2x+y-6=06、设点P(3,2)是圆(x-2)2+(y-1)2=4内部一点,则以P为
中点的弦所在的直线方程___________________.Cx+y-5=0【基础知识】直线与圆的位置关系:※直线与圆相离※直线与圆相切※直线与圆相交XYO几何 d>r交点个数0代数△﹤0 d=r1△=0 d
3.pAB1.已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0当直线l
被C截得的弦长为 时,则a=( )
(A) (B) (C) (D) C.CLABD能力提升:2. 圆(x-3)2+(y+5)2=50被直线4x-3y=2截得
的弦长是________.能力提升103.直线 截圆x2+y2=4所得劣弧
所对圆心角大小为_______.圆心到直线距离 d=OABxy得∠AOB=2∠MOA=600能力提升能力提升Ax-y-3=0小结:1.圆的弦心距、半径、弦长的一半构成一个直角
三角形,在求圆的弦长时要利用到;2.求圆的切线方程时,一般是利用圆心到切线的
距离等于圆的半径。3.经过圆外一点作圆的切线有两条,特别要注意
是否有斜率不存在的直线
