字母表示数

课件27张PPT。1只青蛙1张嘴，2只眼睛4条腿，1声扑通跳下水；
2只青蛙2张嘴，4只眼睛8条腿，2声扑通跳下水；
3只青蛙3张嘴，6只眼睛12条腿，3声扑通跳下水；
………….
你觉得这首歌唱得完吗？你们能否用字母表示这首儿歌？1只青蛙1张嘴，2只眼睛4条腿，1声扑通跳下水；
2只青蛙2张嘴，4只眼睛8条腿，2声扑通跳下水；
3只青蛙3张嘴，6只眼睛12条腿，3声扑通跳下水；
………….
n只青蛙 张嘴， 只眼睛 条腿， 声扑通跳下水.
n2n4nn想一个自然数×5得到的数的个位数字一定是0程序加工机第一节字母能表示什么　
1.某班同学去动物园参观，每张门票5元，全班50人，需要门票多少元？
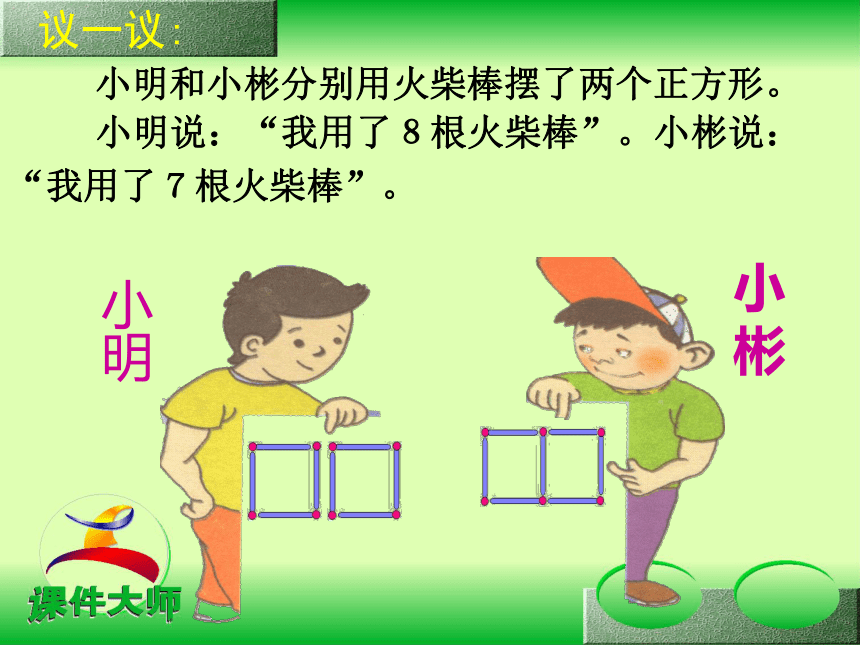
2.某小区要建一个半径为12米的圆形花圃，需占地多少平方米？问题如果把问题1中的50人改成M人，问题2中的半径改为R，答案又是什么？ 2008年奥运会将在我国北京举行。为了迎接北京奥运会，小李同学设想在学校操场上搭一行2008个正方形,怎么搭呢？需要多少根火柴? 　 小明说：“我用了８根火柴棒”。小彬说：
“我用了７根火柴棒”。
议一议:小明和小彬分别用火柴棒摆了两个正方形。想一想: 如果我们按小明的摆法搭一行正方形，那么所用的火柴棒的根数与所搭的正方形的个数之间有什么关系?火柴棒的根数
= 4×正方形的个数所以，
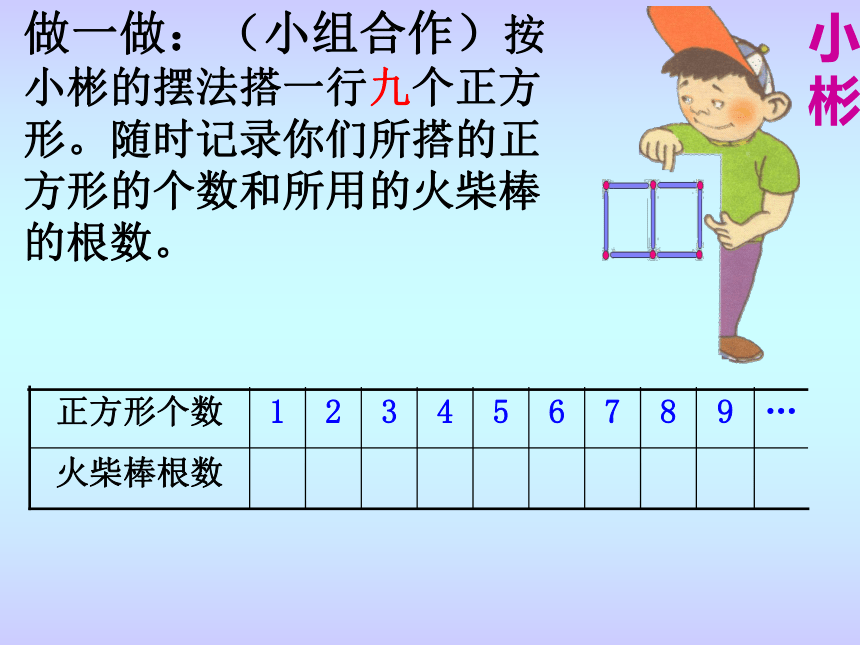
摆 n 个正方形需要 4n 根火柴。搭n个正方形需要多少根火柴？做一做：（小组合作）按小彬的摆法搭一行九个正方形。随时记录你们所搭的正方形的个数和所用的火柴棒的根数。　…2825221916131074议一议：（1）当正方形个数为10个时，火柴根数是多少？（2）当正方形个数为100个时，火柴根数是多少？（3）当正方形个数为X个时，火柴根数 是多少？（4）你发现正方形的个数与火柴的根数之间有何规律？(请与小组的同学互相交流)　　方法：以第一个搭的正方形为基础，然后每增加三根火柴棒，便多一个正方形。………正方形的个数火柴根数12310100…x……44+34+3+34+3+3+…+34+3+3+…+34+3+3+…+3[即4+3（x-1）]…9个99个（x-1）个　　方法：把所搭正方形的火柴棒分三部分考虑（上面一排、下面一排和竖直方向一排）
例：（４个正方形）思考：　①三个部分的火柴棒的根数分别与正方形的个数存在什么样的关系？②当搭的正方形为100个时，火柴棒的根数是多少？…100个共有：
100+100+（100+1）=301（根）③当搭的正方形为X个时，火柴棒的根数是多少？X个共有：X+X+（X+1）（根）方法：…X个正方形则共有：（1+3X）（根）以第一根火柴为基础，然后每增加三根火柴棒，便多一个正方形。
做一做：　　（1）根据你找到的计算方法，搭2008个这样的正方形需要　　　 根火柴棒。6025①４＋３（Ｘ－１）；
②Ｘ＋Ｘ＋（Ｘ＋１）；
③１＋３Ｘ；等等。　　以后，为了方便表达与交流，通常会用象这样含有字母的式子来表示一些数学规律。（注意在这些式子中，我们要明确字母表示的意义）　　由上我们知道，当用Ｘ来表示小正方形的个数时，火柴棒根数的计算方法有多种。如：字母能表示什么？字母可表示任何数(字母表示数在具体情形有具体意义)你还能举出字母表示数 的其它例子吗?小组比赛：在小学我们学过用字母表示数的运算律，以及一些图形的周长、面积和体积的公式。比一比，看那个小组写的多。并说明字母表示什么。(限时3分钟)１、运算律：
① 加法交换律: a+b=b+a；
② 加法结合律: (a+b)+c=a+(b+c)；
③ 乘法交换律: ab = ba；
④ 乘法结合律: (ab)c=a(bc)；
⑤ 分配率: a(b+c)=ab+ac
(a、b、c表示任何数）练习一： 填空（口答）1、每包书有12册，n包书有________册。2、棱长是a厘米的正方体的体积是________立方厘米。3、温度由t℃下降2℃后是_______℃。(t-2)a312n练习二： 填空1、明明步行上学，速度为v米/秒；亮亮骑自行车上学，速度是明明的3倍，则亮亮的速度可以表示为_______米/秒。2、如图，用字母表示图中阴影部分的面积为_________。3vmn-pq1、小刚上学步行速度为v千米/小时,若他家到学校
路程为5千米,则他上学要走 小时.5
v2、某种瓜子单价16元/千克,则m千克需要 元。16m3、同学家有只母鸡,每天下蛋2只,y天下蛋 只。2y4、一打铅笔有12支，n打铅笔 支。12n5 、小明今年6岁,再过a年,小明 岁.(a+6)练习(三）(二）用语言正确表达下列各字母表示的式子的含义，并
讨论字母取值范围。（1）a+(-a)=0互为相反的两数和为零（a为任意有理数）（a≠0）互为倒数的两数积为1零与任何数相加得原数（a为任意有理数）（a为任意有理数）零与任何数相乘得零任何数与1相乘得原数（a为任意有理数）正数和零的绝对值是它本身（a≥0）（3）a+0=a（4）0×a =0（5）a×1=a（6）｜a｜=a（4）观察下列各式，你会发现什么规律？
3×5=15 而15=42-1
5×7=35 而35=62-1
7×9=63 而63=82-1
…… ……
如果用n-1表示前一个因数，则后一个因数可表示为_______;你能用一个等式表示出上面的规律吗？n+1(n-1)(n+1)=n2-1课堂小结:1、今天这节课研究的主要内容：
用字母表示数
2、为什么要用字母来表示数？
使数量之间的关系看上去
更加简明，更加具有普遍意义。
3、用字母表示实际问题时，要注意字母的取值范围。
A= x + y + z成
功艰苦的劳动 正确的方法 少说空话 爱因斯坦成功秘诀: