人教B版高中数学必修一第二章2.1.2函数的表示方法(共25张PPT)
文档属性
| 名称 | 人教B版高中数学必修一第二章2.1.2函数的表示方法(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-03 00:00:00 | ||
图片预览






文档简介
课件25张PPT。§1.2.2 函数的表示法 函数的三种表示方法解析法:用数学表达式表示两个变量之间的对应关系.
图象法:用图象表示两个变量之间的对应关系.
列表法:列出表格来表示两个变量之间的对应关系.
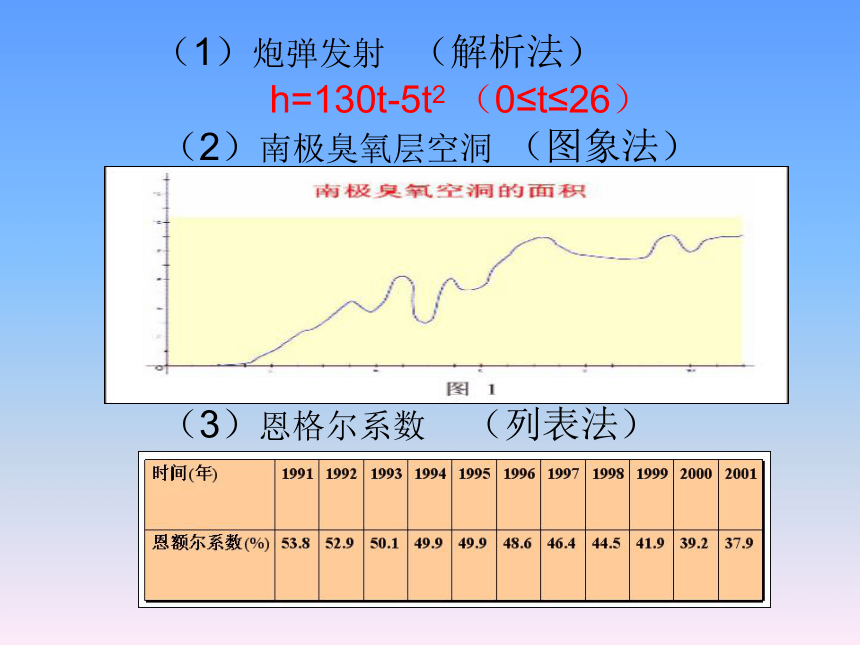
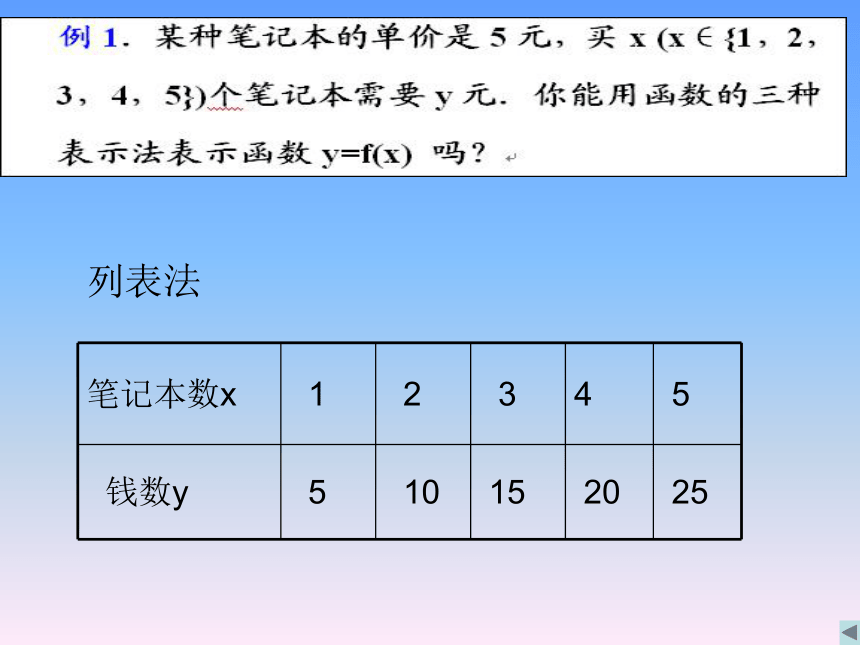
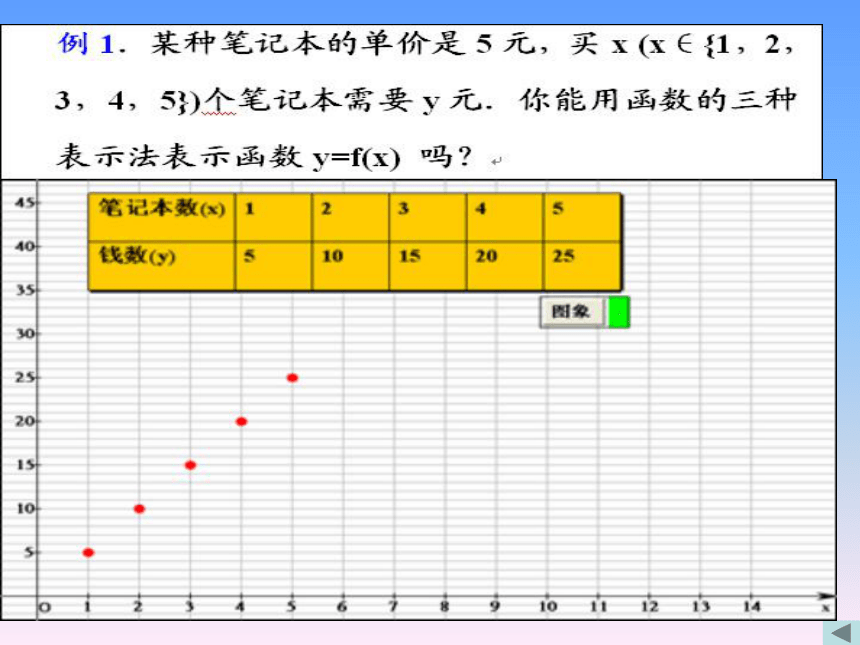
(1)炮弹发射(解析法)h=130t-5t2 (0≤t≤26)(2)南极臭氧层空洞(图象法)(3)恩格尔系数(列表法)解析法y=5x注:用解析法必须注明函数的定义域。列表法三种表示方法的特点解析法的特点:简明、全面地概括了变
量间的关系;可以通过用解析式求出任意
一个自变量所对应的函数值。列表法的特点:不通过计算就可以直接
看出与自变量的值相对应的函数值。图像法的特点:直观形象地表示出函数
的变化情况 ,有利于通过图形研究函数的某些性质。 例2.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:设测试序号为X,成绩为Y,
(1)每位同学的成绩Y与测试序号X之间的函数关系能用解析法表示吗?图象法呢?(2)若要对这三位同学在高一学年度的数学学习情况做一个分析,选用那种方法比较恰当?
解析法1.求下列函数的解析式。
(1)已知函数f(x)为一次函数,且f[f(x)]=4x-1,求f(x)。
(2)已知函数f(x-1)= -3,求f(x)2.若f(x)满足关系式 f(x)-2f(1/x)=3x,求f(x)
变式 设f(x)是R上的函数,且满足f(0)=1 ,并且对任意实数x,y,有f(x-y)=f(x)-y(2x-y+1),求f(x)3.(1)已知函数f(x)的定义域是[0,1],求f( +1)的定义域.
. (2)已知函数f(x+1)的定义域是[0,1] ,求f(x)的定义域
. (3)已知函数f(2x-1)的定义域是[0,1] ,求f(1-3x)的定义域
图像法1.作出下列函数的图像,并求出其值域。
(1)y=2x+1 (2)y= 2 -4x-3 x [1,5]
(3)y=- +2x (4)y=1/x (x>1)2.作出函数y= 的图象例4.某市“招手即停”公共汽车的票价按下列规则制定:
(1) 5公里以内(含5公里),票价2元;
(2) 5公里以上,每增加5公里,票价增加1元(不足5公里
按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价x与
里程y之间的函数解析式,并画出函数的图象.解:设票价为里程为,由题意可知,自变量的取值范围是(0,20],由票价制定规则,可以得到函数解析式为:问:此函数能用列表法表示吗?注意:分段函数是一个函数,自变量所在区间变化,对应关系也随之变化。注意:1、有些函数在它的定义域中,对于自变量x的不同取值范围,
对应关系不同,这种函数通常称为分段函数。分段函数的表
达式虽然不止一个,但它不是几个函数,而是一个函数。
2、分段函数的定义域是各段定义域的并集,值域是各段值域的
并集。
3、函数图象不一定是光滑曲线(直线),还可以是一些孤
立的点、一些线段、一段曲线等。 分段函数1.函数 的定义域是-------------
2.已知函数
(1)求 f[f(f(x))]的值
(2)若f(x)=2,求x的值
(3)若f(x)>2,求x的取值范围3.已知函数y=f(x)的图象如图,由两条射线和抛物线的一部分组成,求函数y=f(x)的解析式函数的推广——映射函数是“两个数集间的一种确定的对应关系”。当我们将数集扩展到任意的集合时,就可以得到映射的概念。映射定义:
设A,B是两个非空的集合,如果按某一个确定的对应关系f , 使对于集合A中的任意一个元素X ,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射。映射的判断:如果集合A中的任何一个元素,按照对应关系f,在集
合B中都有唯一的元素和它对应,那么这个对应就是映
射,否则就不是映射。方向不同,映射也不同。象与原象:映射是从原象集合到象集的对应。判断以下关系是否为映射?请说出映射中的对应法则以及象与原象。小结映射与函数的相同点和不同点
(1)相同点:
①函数与映射都是两个集合中的元素的对应;
②函数与映射分别都有三个要素;
③函数映射的对应都具有方向性;
④函数中的两个集合与映射中两个集合都是非空的;
⑤对应类型只有:一对一,或多对一
(2)不同点:
①函数是一种特殊的映射,映射是函数的扩展;
②函数中的两个集合是非空的数集,映射中的两个集合的元素
是任意的。章节小结:
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表
示法来 表示函数;
(3)注意分段函数的表示方法及其图象的画法。
(4)映射的理解
图象法:用图象表示两个变量之间的对应关系.
列表法:列出表格来表示两个变量之间的对应关系.
(1)炮弹发射(解析法)h=130t-5t2 (0≤t≤26)(2)南极臭氧层空洞(图象法)(3)恩格尔系数(列表法)解析法y=5x注:用解析法必须注明函数的定义域。列表法三种表示方法的特点解析法的特点:简明、全面地概括了变
量间的关系;可以通过用解析式求出任意
一个自变量所对应的函数值。列表法的特点:不通过计算就可以直接
看出与自变量的值相对应的函数值。图像法的特点:直观形象地表示出函数
的变化情况 ,有利于通过图形研究函数的某些性质。 例2.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:设测试序号为X,成绩为Y,
(1)每位同学的成绩Y与测试序号X之间的函数关系能用解析法表示吗?图象法呢?(2)若要对这三位同学在高一学年度的数学学习情况做一个分析,选用那种方法比较恰当?
解析法1.求下列函数的解析式。
(1)已知函数f(x)为一次函数,且f[f(x)]=4x-1,求f(x)。
(2)已知函数f(x-1)= -3,求f(x)2.若f(x)满足关系式 f(x)-2f(1/x)=3x,求f(x)
变式 设f(x)是R上的函数,且满足f(0)=1 ,并且对任意实数x,y,有f(x-y)=f(x)-y(2x-y+1),求f(x)3.(1)已知函数f(x)的定义域是[0,1],求f( +1)的定义域.
. (2)已知函数f(x+1)的定义域是[0,1] ,求f(x)的定义域
. (3)已知函数f(2x-1)的定义域是[0,1] ,求f(1-3x)的定义域
图像法1.作出下列函数的图像,并求出其值域。
(1)y=2x+1 (2)y= 2 -4x-3 x [1,5]
(3)y=- +2x (4)y=1/x (x>1)2.作出函数y= 的图象例4.某市“招手即停”公共汽车的票价按下列规则制定:
(1) 5公里以内(含5公里),票价2元;
(2) 5公里以上,每增加5公里,票价增加1元(不足5公里
按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价x与
里程y之间的函数解析式,并画出函数的图象.解:设票价为里程为,由题意可知,自变量的取值范围是(0,20],由票价制定规则,可以得到函数解析式为:问:此函数能用列表法表示吗?注意:分段函数是一个函数,自变量所在区间变化,对应关系也随之变化。注意:1、有些函数在它的定义域中,对于自变量x的不同取值范围,
对应关系不同,这种函数通常称为分段函数。分段函数的表
达式虽然不止一个,但它不是几个函数,而是一个函数。
2、分段函数的定义域是各段定义域的并集,值域是各段值域的
并集。
3、函数图象不一定是光滑曲线(直线),还可以是一些孤
立的点、一些线段、一段曲线等。 分段函数1.函数 的定义域是-------------
2.已知函数
(1)求 f[f(f(x))]的值
(2)若f(x)=2,求x的值
(3)若f(x)>2,求x的取值范围3.已知函数y=f(x)的图象如图,由两条射线和抛物线的一部分组成,求函数y=f(x)的解析式函数的推广——映射函数是“两个数集间的一种确定的对应关系”。当我们将数集扩展到任意的集合时,就可以得到映射的概念。映射定义:
设A,B是两个非空的集合,如果按某一个确定的对应关系f , 使对于集合A中的任意一个元素X ,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射。映射的判断:如果集合A中的任何一个元素,按照对应关系f,在集
合B中都有唯一的元素和它对应,那么这个对应就是映
射,否则就不是映射。方向不同,映射也不同。象与原象:映射是从原象集合到象集的对应。判断以下关系是否为映射?请说出映射中的对应法则以及象与原象。小结映射与函数的相同点和不同点
(1)相同点:
①函数与映射都是两个集合中的元素的对应;
②函数与映射分别都有三个要素;
③函数映射的对应都具有方向性;
④函数中的两个集合与映射中两个集合都是非空的;
⑤对应类型只有:一对一,或多对一
(2)不同点:
①函数是一种特殊的映射,映射是函数的扩展;
②函数中的两个集合是非空的数集,映射中的两个集合的元素
是任意的。章节小结:
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表
示法来 表示函数;
(3)注意分段函数的表示方法及其图象的画法。
(4)映射的理解
