人教版必修1重点 3.2.1 几类不同增长的函数模型 课件(共47张PPT)
文档属性
| 名称 | 人教版必修1重点 3.2.1 几类不同增长的函数模型 课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 08:49:38 | ||
图片预览






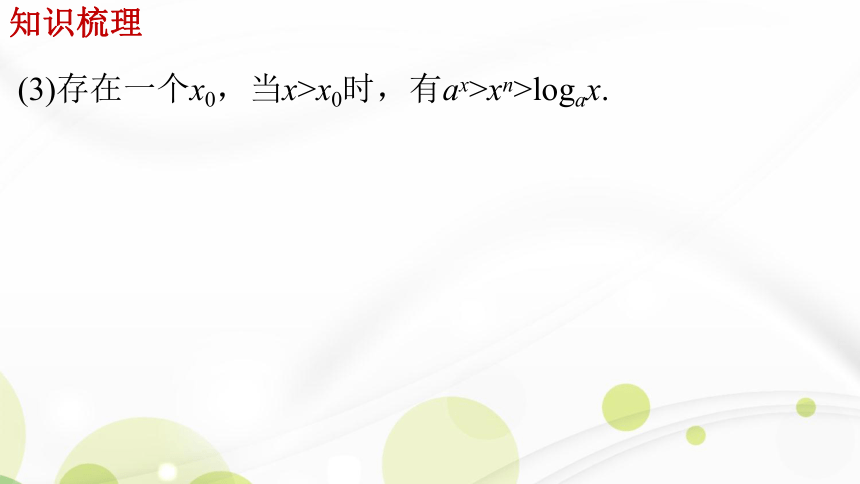



文档简介
(共47张PPT)
3.2.1 几类不同增长的函数模型
人教版必修1
3.2.1 几类不同增长的函数模型
1.理解直线上升、指数爆炸、对数增长的含义.(重点)
2.区分指数函数、对数函数以及幂函数增长速度的差异.
(易混点)
3.会选择适当的函数模型分析和解决一些实际问题.
(难点)
学习目标
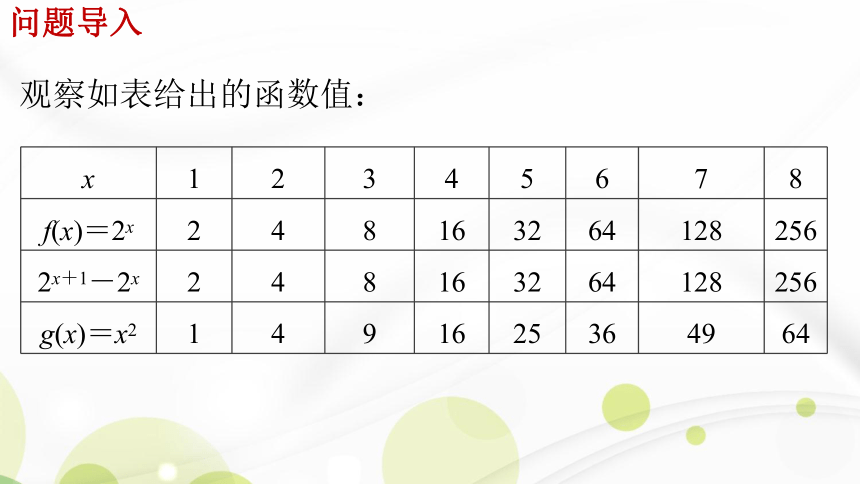
x 1 2 3 4 5 6 7 8
f(x)=2x 2 4 8 16 32 64 128 256
2x+1-2x 2 4 8 16 32 64 128 256
g(x)=x2 1 4 9 16 25 36 49 64
观察如表给出的函数值:
问题导入
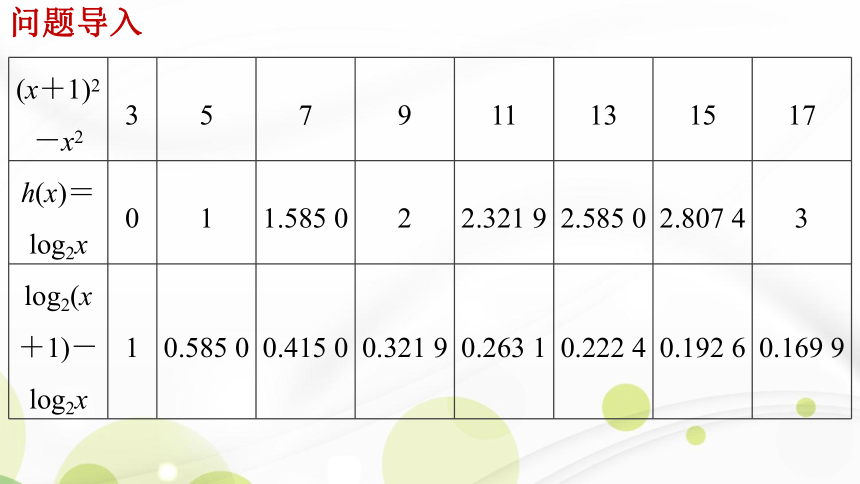
(x+1)2-x2 3 5 7 9 11 13 15 17
h(x)=log2x 0 1 1.585 0 2 2.321 9 2.585 0 2.807 4 3
log2(x+1)-log2x 1 0.585 0 0.415 0 0.321 9 0.263 1 0.222 4 0.192 6 0.169 9
问题导入
问题1:函数f(x),g(x),h(x)随着x的增大,函数值有什么共同的变化趋势?
【答案】函数f(x),g(x),h(x)随着x的增大,函数值增大.
问题2:函数f(x),g(x),h(x)增长的速度有什么不同?
【答案】各函数增长的速度不同,其中f(x)=2x增长得最快,其次是g(x)=x2,最慢的是h(x)=log2x.
问题导入
知识梳理
1.三种函数模型的性质
函数 性质 y=ax(a>1) y=logax(a>1) y=xn(n>0)
在(0,+∞)上 的增减性 增函数 增函数 增函数
图象的变化 随x的增大逐渐与y轴平行 随x的增大逐渐与x轴平行 随n值的不同而不同
知识梳理
2.三种函数增长速度的比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但增长进度不同,且不在同一个“档次”上.
(2)随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度越来越慢.
知识梳理
(3)存在一个x0,当x>x0时,有ax>xn>logax.
预习自测
判断(正确的打“√”,错误的打“×”)
(1)当x增加一个单位时,y增加或减少的量为定值,则y是x的一次函数.( )
(2)函数y=衰减的速度越来越慢.( )
(3)不存在一个实数m,使得当x>m时,1.1x>x100.( )
【解析】 (1)√.因为一次函数的图象是直线,所以当x增加一个单位时,
y增加或减少的量为定值.
(2)√.由函数y= 的图象可知其衰减的速度越来越慢.
(3)×.根据指数函数和幂函数增长速度的比较可知存在一个实数m,使得当x>m时,1.1x>x100.
【答案】 (1)√ (2)√ (3)×
预习自测
例1 (1)下列函数中,增长速度最快的是( )
A.y=2 016x B.y=x2 016
C.y=log2 016x D.y=2 016x
类型1 函数模型的增长差异
合作学习
A
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
(2)四个自变量y1,y2,y3,y4随变量x变化的数据如下表:
则关于x呈指数型函数变化的变量是________.
合作学习
y2
【解析】 (1)比较幂函数、指数函数与对数函数可知,指数函数增长速度最快,故选A.
(2)以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.故填y2.
合作学习
1.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,形象地称为“指数爆炸”.
2.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢.
3.幂函数模型y=xn(n>0)的增长速度介于指数增长和对数增长之间.
名师指导
1.下列函数中随x的增大而增长速度最快的是( )
A.y=ex B.y=100ln x
C.y=x100 D.y=100·2x
【解析】 指数函数y=ax,在a>1时呈爆炸式增长,并且随a值的增大,增长速度越快,应选A.
【答案】 A
跟踪训练
类型2 根据函数图象确定函数模型
例2 函数f(x)=2x和g(x)=x3的图象如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
合作学习
(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断f(6),g(6),f(2 016),g(2 016)的
大小.
合作学习
解: (1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)∵f(1)>g(1),f(2)<g(2),f(9)<g(9),f(10)>g(10),
∴1<x1<2,9<x2<10,
∴x1<6<x2,2 016>x2.
从图象上可以看出,当x1<x<x2时,f(x)<g(x),
∴f(6)<g(6);当x>x2时,f(x)>g(x),
合作学习
∴f(2 016)>g(2 016).
又g(2 016)>g(6),
∴f(2 016)>g(2 016)>g(6)>f(6).
合作学习
根据函数图象判断增长函数模型时,通常是根据函数图象上升的快慢来判断,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的函数是对数函数,中间的是幂函数.
名师指导
2.函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
跟踪训练
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
解:(1)C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lg x.
(2)当xf(x);当x1g(x);
当x>x2时,g(x)>f(x);
当x=x1或x=x2时,f(x)=g(x).
跟踪训练
探究点 函数模型的选择
探究1 在我们学习过的函数中,哪些函数是其定义域上的单调函数?
【答案】 一次函数、指数函数、对数函数.
探究点 函数模型的选择
探究2 在选择函数模型时,若随着自变量的变大、函数值增加得速度急剧变化,应选择哪个函数模型?若变化的速度很平缓,应选择哪个函数模型?
【答案】 前者应选择指数函数模型,后者选择对数函数模型.
例3 某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5~8千美元的地区销售该公司A饮料的情况调查时发现:该饮料在人均GDP处于中等的地区销售量最多,然后向两边递减.
(1)下列几个模拟函数中:①y=ax2+bx;②y=kx+b;
③y=logax+b;④y=ax+b(x表示人均GDP,单位:千美元,y表示年人均A饮料的销售量,单位:L).
用哪个模拟函数来描述人均A饮料销售量与地区的人均
GDP关系更合适?说明理由;
(2)若人均GDP为1千美元时,年人均A饮料的销售量为2 L,人均GDP为4千美元时,年人均A饮料的销售量为5 L,把
(1)中你所选的模拟函数求出来,并求出各个地区中,年人均A饮料的销售量最多是多少?
解: (1)用①来模拟比较合适.因为该饮料在人均GDP处于中等的地区销售量最多,然后向两边递减.而②,③,④表示的函数在区间上是单调函数,所以②,③,④都不合适,故用①来模拟比较合适.
(2)因为人均GDP为1千美元时,年人均A饮料的销量为2升;人均GDP为4千美元时,年人均A饮料的销量为5升,把x=1,y=2;x=4,y=5代入到y=ax2+bx,得解得a=-,b= ,
所以函数解析式为y=- x2+ x.(x∈[0.5,8])
∵y=- x2+ x=- (x- )2+,
∴当x= 时,年人均A饮料的销售量最多是 L.
不同的函数模型能刻画现实世界中不同的变化规律
1.线性函数增长模型适合于描述增长速度不变的变化规律.
2.指数函数增长模型适合于描述增长速度急剧的变化规律.
3.对数函数增长模型适合于描述增长速度平缓的变化规律.
4.幂函数增长模型适合于描述增长速度一般的变化规律.
名师指导
3.某化工厂开发研制了一种新产品,在前三个月的月生产量依次为100t,120t,130t.为了预测今后各个月的生产量,需要以这三个月的月产量为依据,用一个函数来模拟月产量y(t)与月序数x之间的关系.对此模拟函数可选用二次函数y=f(x)=ax2+bx+c(a,b,c均为待定系数,x∈N*)或函数y=g(x)=pqx+r(p,q,r均为待定系数,x∈N*),
跟踪训练
现在已知该厂这种新产品在第四个月的月产量为137t,则选用这两个函数中的哪一个作为模拟函数较好?
跟踪训练
跟踪训练
跟踪训练
f(4)=-5×42+35×4+70=130(t),g(4)=-80×0.54+140=135(t).与f(4)相比,g(4)在数值上更为接近第四个月的实际月产量,所以②式作为模拟函数比①式更好,故选用函数y=g(x)=pqx+r作为模拟函数较好.
1.如下表是函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型( )
课堂检测
x 4 5 6 7 8 9 10
y 15 17 19 21 23 25 27
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
【解析】 自变量每增加1函数值增加2,函数值的增量是均匀的,故为一次函数模型.故选A.
【答案】 A
课堂检测
2.下列函数中,随x的增大,增长速度最快的是( )
A.y=1 B.y=x
C.y=3x D.y=log3x
【解析】 结合函数y=1,y=x,y=3x及y=log3x的图象可知,随着x的增大,增长速度最快的是y=3x.
【答案】 C
课堂检测
3.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润与时间的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
课堂检测
【解析】 结合“直线上升,对数增长,指数爆炸”可知,对数型函数符合题设条件,故选D.
【答案】 D
课堂检测
4.生活经验告诉我们,当水注入容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应________;B对应________;C对应________;D对应________.
课堂检测
【解析】 A容器下粗上细,水高度的变化先慢后快,故与(4)对应;B容器为球形,水高度变化为快—慢—快,应与(1)对应;C,D容器都是柱形的,水高度的变化速度都应是直线型,但C容器细,D容器粗,故水高度的变化为:C容器快,与(3)对应,D容器慢,与(2)对应.
【答案】 (4) (1) (3) (2)
课堂检测
5.函数f(x)=1.1x,g(x)=ln x+1,h(x)=x的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
课堂检测
解:由指数爆炸、对数增长、幂函数增长的差异可得曲线C1对应的函数是f(x)=1.1x,曲线C2对应的函数是h(x)=,曲线C3对应的函数是g(x)=ln x+1.
由题图知,当x<1时,f(x)>h(x)>g(x);
当1g(x)>h(x);
当ef(x)>h(x);
课堂检测
当ah(x)>f(x);
当bg(x)>f(x);
当cf(x)>g(x);当x>d时,f(x)>h(x)>g(x).
课堂检测
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2.1 几类不同增长的函数模型
人教版必修1
3.2.1 几类不同增长的函数模型
1.理解直线上升、指数爆炸、对数增长的含义.(重点)
2.区分指数函数、对数函数以及幂函数增长速度的差异.
(易混点)
3.会选择适当的函数模型分析和解决一些实际问题.
(难点)
学习目标
x 1 2 3 4 5 6 7 8
f(x)=2x 2 4 8 16 32 64 128 256
2x+1-2x 2 4 8 16 32 64 128 256
g(x)=x2 1 4 9 16 25 36 49 64
观察如表给出的函数值:
问题导入
(x+1)2-x2 3 5 7 9 11 13 15 17
h(x)=log2x 0 1 1.585 0 2 2.321 9 2.585 0 2.807 4 3
log2(x+1)-log2x 1 0.585 0 0.415 0 0.321 9 0.263 1 0.222 4 0.192 6 0.169 9
问题导入
问题1:函数f(x),g(x),h(x)随着x的增大,函数值有什么共同的变化趋势?
【答案】函数f(x),g(x),h(x)随着x的增大,函数值增大.
问题2:函数f(x),g(x),h(x)增长的速度有什么不同?
【答案】各函数增长的速度不同,其中f(x)=2x增长得最快,其次是g(x)=x2,最慢的是h(x)=log2x.
问题导入
知识梳理
1.三种函数模型的性质
函数 性质 y=ax(a>1) y=logax(a>1) y=xn(n>0)
在(0,+∞)上 的增减性 增函数 增函数 增函数
图象的变化 随x的增大逐渐与y轴平行 随x的增大逐渐与x轴平行 随n值的不同而不同
知识梳理
2.三种函数增长速度的比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但增长进度不同,且不在同一个“档次”上.
(2)随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度越来越慢.
知识梳理
(3)存在一个x0,当x>x0时,有ax>xn>logax.
预习自测
判断(正确的打“√”,错误的打“×”)
(1)当x增加一个单位时,y增加或减少的量为定值,则y是x的一次函数.( )
(2)函数y=衰减的速度越来越慢.( )
(3)不存在一个实数m,使得当x>m时,1.1x>x100.( )
【解析】 (1)√.因为一次函数的图象是直线,所以当x增加一个单位时,
y增加或减少的量为定值.
(2)√.由函数y= 的图象可知其衰减的速度越来越慢.
(3)×.根据指数函数和幂函数增长速度的比较可知存在一个实数m,使得当x>m时,1.1x>x100.
【答案】 (1)√ (2)√ (3)×
预习自测
例1 (1)下列函数中,增长速度最快的是( )
A.y=2 016x B.y=x2 016
C.y=log2 016x D.y=2 016x
类型1 函数模型的增长差异
合作学习
A
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
(2)四个自变量y1,y2,y3,y4随变量x变化的数据如下表:
则关于x呈指数型函数变化的变量是________.
合作学习
y2
【解析】 (1)比较幂函数、指数函数与对数函数可知,指数函数增长速度最快,故选A.
(2)以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.故填y2.
合作学习
1.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,形象地称为“指数爆炸”.
2.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢.
3.幂函数模型y=xn(n>0)的增长速度介于指数增长和对数增长之间.
名师指导
1.下列函数中随x的增大而增长速度最快的是( )
A.y=ex B.y=100ln x
C.y=x100 D.y=100·2x
【解析】 指数函数y=ax,在a>1时呈爆炸式增长,并且随a值的增大,增长速度越快,应选A.
【答案】 A
跟踪训练
类型2 根据函数图象确定函数模型
例2 函数f(x)=2x和g(x)=x3的图象如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
合作学习
(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断f(6),g(6),f(2 016),g(2 016)的
大小.
合作学习
解: (1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)∵f(1)>g(1),f(2)<g(2),f(9)<g(9),f(10)>g(10),
∴1<x1<2,9<x2<10,
∴x1<6<x2,2 016>x2.
从图象上可以看出,当x1<x<x2时,f(x)<g(x),
∴f(6)<g(6);当x>x2时,f(x)>g(x),
合作学习
∴f(2 016)>g(2 016).
又g(2 016)>g(6),
∴f(2 016)>g(2 016)>g(6)>f(6).
合作学习
根据函数图象判断增长函数模型时,通常是根据函数图象上升的快慢来判断,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的函数是对数函数,中间的是幂函数.
名师指导
2.函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
跟踪训练
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
解:(1)C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lg x.
(2)当x
当x>x2时,g(x)>f(x);
当x=x1或x=x2时,f(x)=g(x).
跟踪训练
探究点 函数模型的选择
探究1 在我们学习过的函数中,哪些函数是其定义域上的单调函数?
【答案】 一次函数、指数函数、对数函数.
探究点 函数模型的选择
探究2 在选择函数模型时,若随着自变量的变大、函数值增加得速度急剧变化,应选择哪个函数模型?若变化的速度很平缓,应选择哪个函数模型?
【答案】 前者应选择指数函数模型,后者选择对数函数模型.
例3 某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5~8千美元的地区销售该公司A饮料的情况调查时发现:该饮料在人均GDP处于中等的地区销售量最多,然后向两边递减.
(1)下列几个模拟函数中:①y=ax2+bx;②y=kx+b;
③y=logax+b;④y=ax+b(x表示人均GDP,单位:千美元,y表示年人均A饮料的销售量,单位:L).
用哪个模拟函数来描述人均A饮料销售量与地区的人均
GDP关系更合适?说明理由;
(2)若人均GDP为1千美元时,年人均A饮料的销售量为2 L,人均GDP为4千美元时,年人均A饮料的销售量为5 L,把
(1)中你所选的模拟函数求出来,并求出各个地区中,年人均A饮料的销售量最多是多少?
解: (1)用①来模拟比较合适.因为该饮料在人均GDP处于中等的地区销售量最多,然后向两边递减.而②,③,④表示的函数在区间上是单调函数,所以②,③,④都不合适,故用①来模拟比较合适.
(2)因为人均GDP为1千美元时,年人均A饮料的销量为2升;人均GDP为4千美元时,年人均A饮料的销量为5升,把x=1,y=2;x=4,y=5代入到y=ax2+bx,得解得a=-,b= ,
所以函数解析式为y=- x2+ x.(x∈[0.5,8])
∵y=- x2+ x=- (x- )2+,
∴当x= 时,年人均A饮料的销售量最多是 L.
不同的函数模型能刻画现实世界中不同的变化规律
1.线性函数增长模型适合于描述增长速度不变的变化规律.
2.指数函数增长模型适合于描述增长速度急剧的变化规律.
3.对数函数增长模型适合于描述增长速度平缓的变化规律.
4.幂函数增长模型适合于描述增长速度一般的变化规律.
名师指导
3.某化工厂开发研制了一种新产品,在前三个月的月生产量依次为100t,120t,130t.为了预测今后各个月的生产量,需要以这三个月的月产量为依据,用一个函数来模拟月产量y(t)与月序数x之间的关系.对此模拟函数可选用二次函数y=f(x)=ax2+bx+c(a,b,c均为待定系数,x∈N*)或函数y=g(x)=pqx+r(p,q,r均为待定系数,x∈N*),
跟踪训练
现在已知该厂这种新产品在第四个月的月产量为137t,则选用这两个函数中的哪一个作为模拟函数较好?
跟踪训练
跟踪训练
跟踪训练
f(4)=-5×42+35×4+70=130(t),g(4)=-80×0.54+140=135(t).与f(4)相比,g(4)在数值上更为接近第四个月的实际月产量,所以②式作为模拟函数比①式更好,故选用函数y=g(x)=pqx+r作为模拟函数较好.
1.如下表是函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型( )
课堂检测
x 4 5 6 7 8 9 10
y 15 17 19 21 23 25 27
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
【解析】 自变量每增加1函数值增加2,函数值的增量是均匀的,故为一次函数模型.故选A.
【答案】 A
课堂检测
2.下列函数中,随x的增大,增长速度最快的是( )
A.y=1 B.y=x
C.y=3x D.y=log3x
【解析】 结合函数y=1,y=x,y=3x及y=log3x的图象可知,随着x的增大,增长速度最快的是y=3x.
【答案】 C
课堂检测
3.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润与时间的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
课堂检测
【解析】 结合“直线上升,对数增长,指数爆炸”可知,对数型函数符合题设条件,故选D.
【答案】 D
课堂检测
4.生活经验告诉我们,当水注入容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应________;B对应________;C对应________;D对应________.
课堂检测
【解析】 A容器下粗上细,水高度的变化先慢后快,故与(4)对应;B容器为球形,水高度变化为快—慢—快,应与(1)对应;C,D容器都是柱形的,水高度的变化速度都应是直线型,但C容器细,D容器粗,故水高度的变化为:C容器快,与(3)对应,D容器慢,与(2)对应.
【答案】 (4) (1) (3) (2)
课堂检测
5.函数f(x)=1.1x,g(x)=ln x+1,h(x)=x的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
课堂检测
解:由指数爆炸、对数增长、幂函数增长的差异可得曲线C1对应的函数是f(x)=1.1x,曲线C2对应的函数是h(x)=,曲线C3对应的函数是g(x)=ln x+1.
由题图知,当x<1时,f(x)>h(x)>g(x);
当1
当e
课堂检测
当a
当b
当c
课堂检测
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
