22.3相似三角形的性质课件
图片预览




文档简介
课件15张PPT。相似三角形性质 安徽省颍上县建颍中学
王小明一、回顾: 1、相似三角形的定义性质? 对应角相等、对应边成比例2、相似比的定义?相似三角形对应边长度之比研究平台相似三角形的对应高的比等于相似比;
相似三角形的对应中线的比等于相似比;
相似三角形的对应角平分线的比等于相似比.
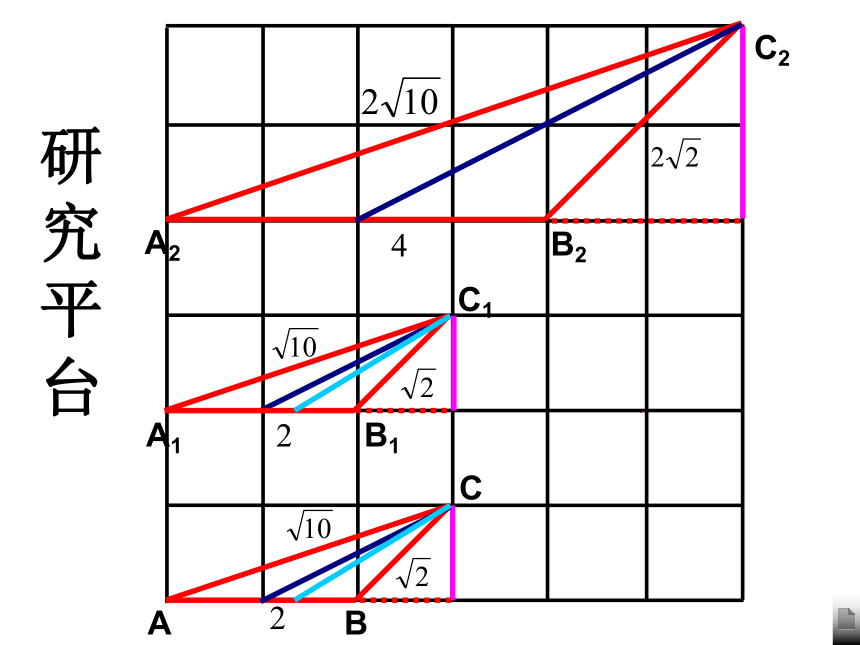
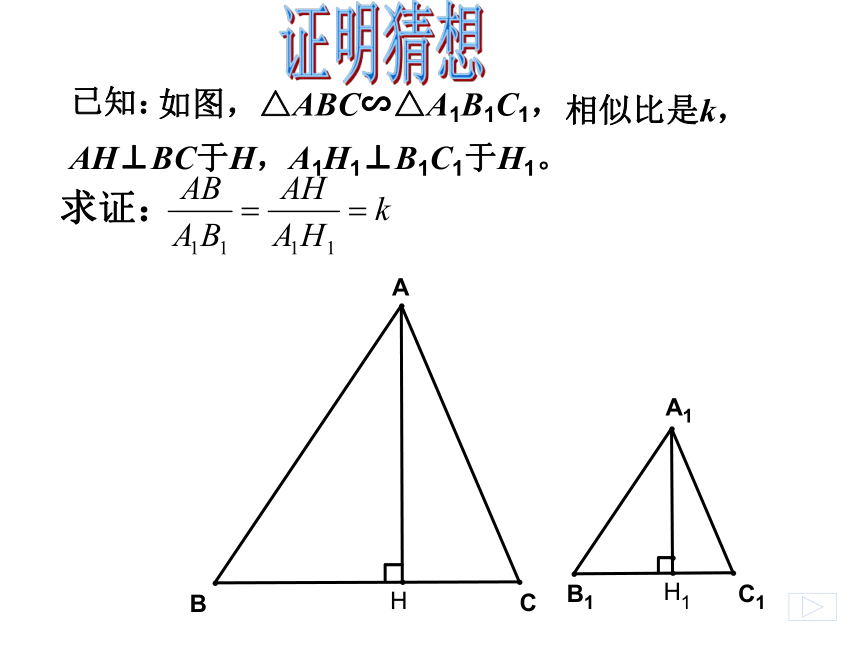
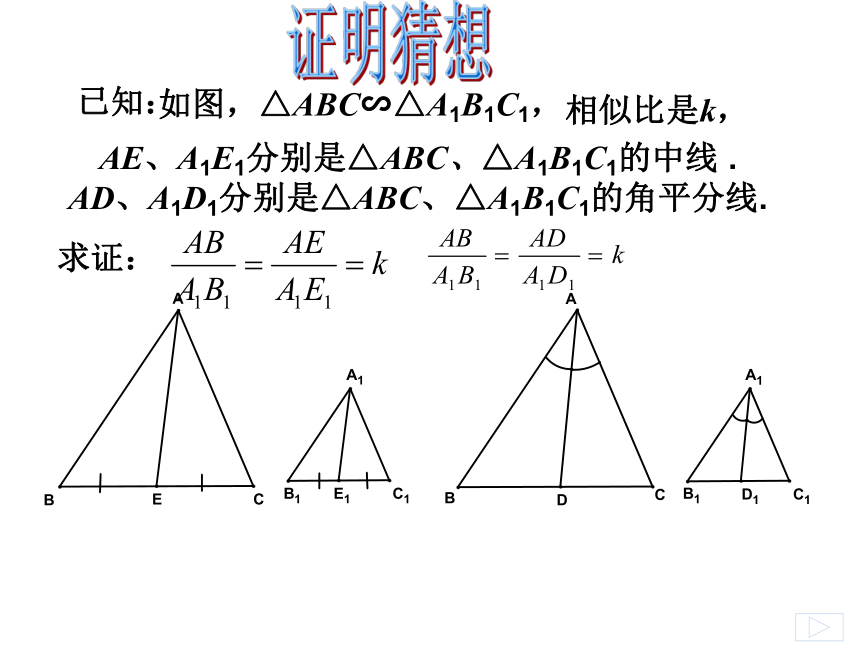
数学猜想 如图,△ABC∽△A1B1C1,求证:证明猜想 已知:相似比是k,AH⊥BC于H,A1H1⊥B1C1于H1。证明猜想 如图,△ABC∽△A1B1C1,求证:已知:相似比是k,AE、A1E1分别是△ABC、△A1B1C1的中线 .
AD、A1D1分别是△ABC、△A1B1C1的角平分线.(猜想加以证明)定理1:1、相似三角形对应边上的高之比等于相似比
2、相似三角形对应边上中线之比等于相似比
3、相似三角形对应角平分线之比等于相似比A2B2C2224研究平台相似三角形的周长的比等于相似比;
相似三角形的面积之比等于相似比平方;
数学猜想 命题:相似三角形的周长的比等于相似比。
相似三角形的面积的比等于相似比的平方。ACDEFGHB 已知:△ABC∽△DEF,相似比为к,C△ABCC△DEF=к求证:S△DEF=к2S△ABC① ②;例2、如图,ΔABC的面积为25,直线DE平行于BC分别交AB、AC于点D、 E。如果ΔADE的面积为9,求 的值1、判断题
⑴相似三角形的中线比等于相似比……( )
⑵两个相似三角形的边长之比等于高之比
…………………………………………( )
××巩固练习2、填空题
⑴已知△ABC∽△A′B′C′的相似比为2︰3,
则它们对应中线的比为 ;
⑵已知两个相似三角形对应高的比是4︰1,
则它们的对应角平分线的比是 ;
⑶已知两个相似三角形对应角平分线的长分别为2 cm
和6cm ,其中一个三角形的周长18cm,则另一个三
角形的周长是 cm。 2︰34︰16或54小结与自主评价⑴今天这节课我们通过探索,学习了什么?
⑵在运用相似三角形性质时,关键是注意什么?
⑶今天,我们在探讨相似三角形的性质的过程中
应用了哪些数学方法?
建颍乡建造一新住宅小区,同时在小区旁筑一条马路。在施工中遇到这样一个问题,小区旁原来有一个面积是64平方米,周长44米的三角形的荒地,由于建筑马路这块地被削去了一块梯形,原荒地的一边AB的长由原来的12米缩短成9米。然后在剩下的荒地上种绿化,你能不用工具测量,计算出现在绿化地面积到底有多大?它的周长是多少?问题:
王小明一、回顾: 1、相似三角形的定义性质? 对应角相等、对应边成比例2、相似比的定义?相似三角形对应边长度之比研究平台相似三角形的对应高的比等于相似比;
相似三角形的对应中线的比等于相似比;
相似三角形的对应角平分线的比等于相似比.
数学猜想 如图,△ABC∽△A1B1C1,求证:证明猜想 已知:相似比是k,AH⊥BC于H,A1H1⊥B1C1于H1。证明猜想 如图,△ABC∽△A1B1C1,求证:已知:相似比是k,AE、A1E1分别是△ABC、△A1B1C1的中线 .
AD、A1D1分别是△ABC、△A1B1C1的角平分线.(猜想加以证明)定理1:1、相似三角形对应边上的高之比等于相似比
2、相似三角形对应边上中线之比等于相似比
3、相似三角形对应角平分线之比等于相似比A2B2C2224研究平台相似三角形的周长的比等于相似比;
相似三角形的面积之比等于相似比平方;
数学猜想 命题:相似三角形的周长的比等于相似比。
相似三角形的面积的比等于相似比的平方。ACDEFGHB 已知:△ABC∽△DEF,相似比为к,C△ABCC△DEF=к求证:S△DEF=к2S△ABC① ②;例2、如图,ΔABC的面积为25,直线DE平行于BC分别交AB、AC于点D、 E。如果ΔADE的面积为9,求 的值1、判断题
⑴相似三角形的中线比等于相似比……( )
⑵两个相似三角形的边长之比等于高之比
…………………………………………( )
××巩固练习2、填空题
⑴已知△ABC∽△A′B′C′的相似比为2︰3,
则它们对应中线的比为 ;
⑵已知两个相似三角形对应高的比是4︰1,
则它们的对应角平分线的比是 ;
⑶已知两个相似三角形对应角平分线的长分别为2 cm
和6cm ,其中一个三角形的周长18cm,则另一个三
角形的周长是 cm。 2︰34︰16或54小结与自主评价⑴今天这节课我们通过探索,学习了什么?
⑵在运用相似三角形性质时,关键是注意什么?
⑶今天,我们在探讨相似三角形的性质的过程中
应用了哪些数学方法?
建颍乡建造一新住宅小区,同时在小区旁筑一条马路。在施工中遇到这样一个问题,小区旁原来有一个面积是64平方米,周长44米的三角形的荒地,由于建筑马路这块地被削去了一块梯形,原荒地的一边AB的长由原来的12米缩短成9米。然后在剩下的荒地上种绿化,你能不用工具测量,计算出现在绿化地面积到底有多大?它的周长是多少?问题:
