2024--2025学年七年级数学上册浙教版 一-三章期中提高练习(含答案)
文档属性
| 名称 | 2024--2025学年七年级数学上册浙教版 一-三章期中提高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 13:44:11 | ||
图片预览



文档简介
一-三章期中提高练习2024--2025学年浙教版七年级数学上册
一、选择题
1.是第五代移动通信技术,网络理论下载速度可以达到每秒以上.用科学记数法表示1300000是( )
A. B. C. D.
2.绝对值等于3的数是( )
A. B.0 C.3 D.3或
3.为加快打造智能网联新能源汽车产业集群,长安、赛力斯、吉利、理想等10家整车企业,200余家核心零部件企业进行联合.小虎所在的生产车间需要加工标准尺寸为4.5mm的零部件,其中(4.5±0.2)mm范围内的尺寸为合格,则下列尺寸的零部件不合格的是( )
A.4.4mm B.4.5mm C.4.6mm D.4.8mm
4.在数,,0,,,,,…(相邻的两个2之间依次多一个0)中,无理数有( )
A.3个 B.4个 C.5个 D.6个
5.64的平方根是
A. 8 B.4 C. D.
6.如图,有理数在数轴上的对应点分别是,若,则的值( )
A.大于 B.小于 C.等于 D.不确定
7.按如图所示的运算程序,能使输出的结果为3的是( )
A. , B. , C. , D. ,
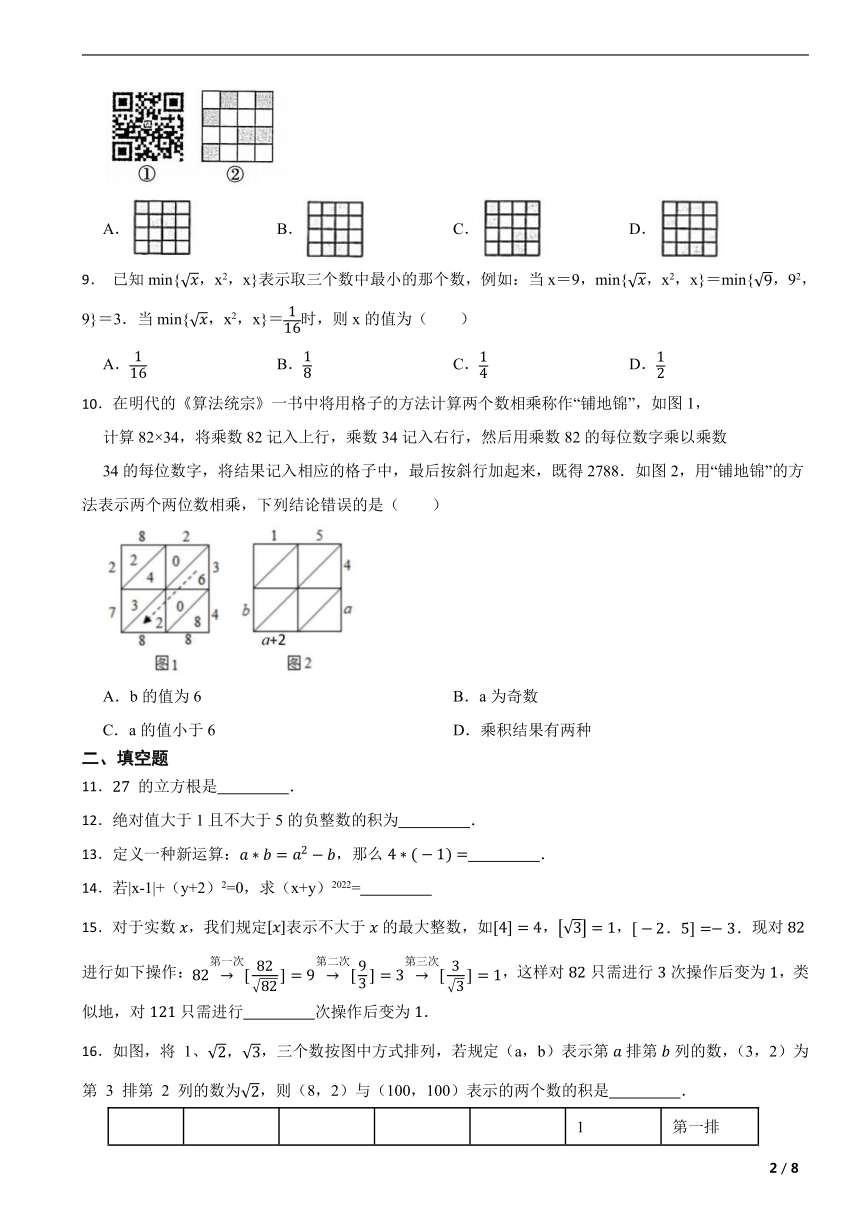
8.利用如图①所示的二维码可以进行身份识别,某校建立了一个身份识别系统,图②是某个学生的识别图案,灰色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为(,如图②中第一行数字从左到右依次为0,1,0,1,序号为表示该生为5班学生,那么表示7班学生的识别图案是( )
A. B. C. D.
9. 已知min{,x2,x}表示取三个数中最小的那个数,例如:当x=9,min{,x2,x}=min{,92,9}=3.当min{,x2,x}=时,则x的值为( )
A. B. C. D.
10.在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”,如图1,
计算82×34,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数
34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地锦”的方法表示两个两位数相乘,下列结论错误的是( )
A.b的值为6 B.a为奇数
C.a的值小于6 D.乘积结果有两种
二、填空题
11. 的立方根是 .
12.绝对值大于1且不大于5的负整数的积为 .
13.定义一种新运算:,那么 .
14.若|x-1|+(y+2)2=0,求(x+y)2022=
15.对于实数,我们规定表示不大于的最大整数,如,,现对进行如下操作:,这样对只需进行次操作后变为,类似地,对只需进行 次操作后变为.
16.如图,将 1、,三个数按图中方式排列,若规定(a,b)表示第排第列的数,(3,2)为第 3 排第 2 列的数为,则(8,2)与(100,100)表示的两个数的积是 .
1 第一排
第二排
第三排
第四排
第五排
…… 第五列 第四列 第三列 第二列 第一列 ……
三、解答题
17.把下列各数填到相应的括号里(只填编号即可)
①;②;③0.5;④1;⑤0;⑥;⑦;⑧
正数:{ …};
分数:{ …};
非负整数:{ …}.
18.如下,小明有4张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题.
1 2
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
19.把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
20. 在有些情况下,不需要计算出结果也能把绝对值符号去掉,例如:;;;.
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:① ;② ;
(2)用简单的方法计算:.
21.出租车司机小李某天上午从家出发,在东西走向的大街上,连续接送六位乘客的行车里程如下(规定向东为正,向西为负,单位:km):,,,,,.
(1)若该出租车耗油量为,则在这个过程中出租车共耗油多少升?
(2)若该出租车的计价标准为行驶路程不超过收费10元,超过的部分按每千米元收费,则小李这天上午共收到车费多少元?
22.已知,则的整数部分为1;而减去其整数部分的差就是的小数部分,则的小数部分为.根据以上的内容,解答下面的问题:
(1)填空:的整数部分是 ,的小数部分是 .
(2)若,其中是m为整数,且0<n<1,求m﹣n的值.
23.如图,在4×4的小正方形组成的图形中有一个阴影部分(阴影部分也是正方形).若每个小正方形的边长为1,点A表示的数为1.
(1)图中正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?
(2)若阴影正方形的边长的值的整数部分为x,小数部分为y,求(y-)x的值.
(3)若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B翻滚到与数轴上的点P重合时,记为第一次翻滚,如图所示,C翻滚到数轴上时,记为第二次翻滚,以此类推,请直接回答:
①点P表示的数为多少?
②是否存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2023重合?
参考答案
1.B
2.D
3.D
4.C
5.C
6.B
7.D
8.D
9.C
解:若则 x<, 不符合最小;
若x2=,x=,当x=-时,x若x=,x2=, x>x2, 不符合x最小.
10.B
解:用“铺地锦”的方法表示两个两位数相乘的格子如下:
∴,或,
∴乘积的结果是两种.
11.3
12.120
13.
14.1
15.3
16.
解:∵每三个数一循环,1、,,
(8,2)在数列中是第(1+7)×7÷2+2=30个,
30÷3=10,
∴(8,2)表示的数正好是第10轮的最后一个,
∴(8,2)表示的数是;
(100,100)在数列中是第(1+99)×99÷2+100=5050个,
5050÷3=16831,
∴(100,100)表示的数正好是第1684轮的第一个数,
∴(100,100)表示的数是1,
∴(8,2)与(100,100)表示的两个数的积是.
17.正数:①③④⑧;分数:①②③⑦⑧;非负整数:④⑤
18.(1)抽和,最大值是15
(2)抽1和,最小值
19.解:,
将下列实数在数轴上表示如下:
用“”连接为:,
20.(1)7+2;
(2)解:
=
=
=
21.(1)解:∵,
∴,
∴在这过程中出租车共耗油升
(2)解:∵接送第一位客人的收费为:10(元),
接送第二位客人的收费为:元,
接送第三位客人的收费为:(元),
接送第四位客人的收费为:元,
接送第五位客人的收费为:(元),
接送第六位客人的收费为:10(元),
∴(元).
∴小李这天上午共收到车费78元.
22.(1)4;
(2)解:∵25<34<36,
∴,即,
∴,
∴,
∵m是整数,且0<n<1,
∴,
∴.
23.(1)解: 正方形ABCD的面积为:16-4××1×3=10;
该正方形的边长为:;
∵9<10<16,
∴,
∴这个值在3与4之间;
(2)解:∵,
∴x=3,y=-3,
∴(y-)3=(-3-)=(-3)3=-27;
(3)解:①∵AB=AP=,
∴点P离开原点得距离为:,
又∵点P在原点得右边,
∴点P表示的数为:1+;
②不存在,理由如下:
假设存在正整数n,则nx+1=2023,
n=2022
=,
∵n为正整数,
∴可得为有理数, 而为无理数,
∴上式等号不成立,即不存在正整数n.
1 / 1
一、选择题
1.是第五代移动通信技术,网络理论下载速度可以达到每秒以上.用科学记数法表示1300000是( )
A. B. C. D.
2.绝对值等于3的数是( )
A. B.0 C.3 D.3或
3.为加快打造智能网联新能源汽车产业集群,长安、赛力斯、吉利、理想等10家整车企业,200余家核心零部件企业进行联合.小虎所在的生产车间需要加工标准尺寸为4.5mm的零部件,其中(4.5±0.2)mm范围内的尺寸为合格,则下列尺寸的零部件不合格的是( )
A.4.4mm B.4.5mm C.4.6mm D.4.8mm
4.在数,,0,,,,,…(相邻的两个2之间依次多一个0)中,无理数有( )
A.3个 B.4个 C.5个 D.6个
5.64的平方根是
A. 8 B.4 C. D.
6.如图,有理数在数轴上的对应点分别是,若,则的值( )
A.大于 B.小于 C.等于 D.不确定
7.按如图所示的运算程序,能使输出的结果为3的是( )
A. , B. , C. , D. ,
8.利用如图①所示的二维码可以进行身份识别,某校建立了一个身份识别系统,图②是某个学生的识别图案,灰色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为(,如图②中第一行数字从左到右依次为0,1,0,1,序号为表示该生为5班学生,那么表示7班学生的识别图案是( )
A. B. C. D.
9. 已知min{,x2,x}表示取三个数中最小的那个数,例如:当x=9,min{,x2,x}=min{,92,9}=3.当min{,x2,x}=时,则x的值为( )
A. B. C. D.
10.在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”,如图1,
计算82×34,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数
34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地锦”的方法表示两个两位数相乘,下列结论错误的是( )
A.b的值为6 B.a为奇数
C.a的值小于6 D.乘积结果有两种
二、填空题
11. 的立方根是 .
12.绝对值大于1且不大于5的负整数的积为 .
13.定义一种新运算:,那么 .
14.若|x-1|+(y+2)2=0,求(x+y)2022=
15.对于实数,我们规定表示不大于的最大整数,如,,现对进行如下操作:,这样对只需进行次操作后变为,类似地,对只需进行 次操作后变为.
16.如图,将 1、,三个数按图中方式排列,若规定(a,b)表示第排第列的数,(3,2)为第 3 排第 2 列的数为,则(8,2)与(100,100)表示的两个数的积是 .
1 第一排
第二排
第三排
第四排
第五排
…… 第五列 第四列 第三列 第二列 第一列 ……
三、解答题
17.把下列各数填到相应的括号里(只填编号即可)
①;②;③0.5;④1;⑤0;⑥;⑦;⑧
正数:{ …};
分数:{ …};
非负整数:{ …}.
18.如下,小明有4张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题.
1 2
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
19.把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
20. 在有些情况下,不需要计算出结果也能把绝对值符号去掉,例如:;;;.
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:① ;② ;
(2)用简单的方法计算:.
21.出租车司机小李某天上午从家出发,在东西走向的大街上,连续接送六位乘客的行车里程如下(规定向东为正,向西为负,单位:km):,,,,,.
(1)若该出租车耗油量为,则在这个过程中出租车共耗油多少升?
(2)若该出租车的计价标准为行驶路程不超过收费10元,超过的部分按每千米元收费,则小李这天上午共收到车费多少元?
22.已知,则的整数部分为1;而减去其整数部分的差就是的小数部分,则的小数部分为.根据以上的内容,解答下面的问题:
(1)填空:的整数部分是 ,的小数部分是 .
(2)若,其中是m为整数,且0<n<1,求m﹣n的值.
23.如图,在4×4的小正方形组成的图形中有一个阴影部分(阴影部分也是正方形).若每个小正方形的边长为1,点A表示的数为1.
(1)图中正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?
(2)若阴影正方形的边长的值的整数部分为x,小数部分为y,求(y-)x的值.
(3)若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B翻滚到与数轴上的点P重合时,记为第一次翻滚,如图所示,C翻滚到数轴上时,记为第二次翻滚,以此类推,请直接回答:
①点P表示的数为多少?
②是否存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2023重合?
参考答案
1.B
2.D
3.D
4.C
5.C
6.B
7.D
8.D
9.C
解:若则 x<, 不符合最小;
若x2=,x=,当x=-时,x
10.B
解:用“铺地锦”的方法表示两个两位数相乘的格子如下:
∴,或,
∴乘积的结果是两种.
11.3
12.120
13.
14.1
15.3
16.
解:∵每三个数一循环,1、,,
(8,2)在数列中是第(1+7)×7÷2+2=30个,
30÷3=10,
∴(8,2)表示的数正好是第10轮的最后一个,
∴(8,2)表示的数是;
(100,100)在数列中是第(1+99)×99÷2+100=5050个,
5050÷3=16831,
∴(100,100)表示的数正好是第1684轮的第一个数,
∴(100,100)表示的数是1,
∴(8,2)与(100,100)表示的两个数的积是.
17.正数:①③④⑧;分数:①②③⑦⑧;非负整数:④⑤
18.(1)抽和,最大值是15
(2)抽1和,最小值
19.解:,
将下列实数在数轴上表示如下:
用“”连接为:,
20.(1)7+2;
(2)解:
=
=
=
21.(1)解:∵,
∴,
∴在这过程中出租车共耗油升
(2)解:∵接送第一位客人的收费为:10(元),
接送第二位客人的收费为:元,
接送第三位客人的收费为:(元),
接送第四位客人的收费为:元,
接送第五位客人的收费为:(元),
接送第六位客人的收费为:10(元),
∴(元).
∴小李这天上午共收到车费78元.
22.(1)4;
(2)解:∵25<34<36,
∴,即,
∴,
∴,
∵m是整数,且0<n<1,
∴,
∴.
23.(1)解: 正方形ABCD的面积为:16-4××1×3=10;
该正方形的边长为:;
∵9<10<16,
∴,
∴这个值在3与4之间;
(2)解:∵,
∴x=3,y=-3,
∴(y-)3=(-3-)=(-3)3=-27;
(3)解:①∵AB=AP=,
∴点P离开原点得距离为:,
又∵点P在原点得右边,
∴点P表示的数为:1+;
②不存在,理由如下:
假设存在正整数n,则nx+1=2023,
n=2022
=,
∵n为正整数,
∴可得为有理数, 而为无理数,
∴上式等号不成立,即不存在正整数n.
1 / 1
同课章节目录
