24.1.4圆周角 教学课件(共33张PPT)初中数学人教版(2012)九年级上册
文档属性
| 名称 | 24.1.4圆周角 教学课件(共33张PPT)初中数学人教版(2012)九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 14:29:46 | ||
图片预览





文档简介
(共33张PPT)
24.1.4圆周角
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
理解圆周角的概念,会叙述并证明圆周角定理
1
理解圆周角与圆心角的关系,并能运用圆周角定理解决简单的几何问题
2
理解掌握圆周角定理的推论及其证明过程和应用
3
理解并掌握圆内接四边形的概念和性质
4
探索新知
Part Two
贰
知识回顾
问题1:什么叫圆心角?指出图中的圆心角,并说说识别圆心角的需要注意什么?
顶点在圆心的角叫圆心角,∠BOC.
注意点:①顶点在圆心上②两条边和圆相交.
A
问题2:弧、弦、圆心角的关系定理是什么?
相等的圆心角所对的弧相等,所对的弦也相等.
相等的弧所对的圆心角相等,所对的弦也相等.
相等的弦所对的圆心角相等,所对的优弧和劣弧也相等.
新课导入
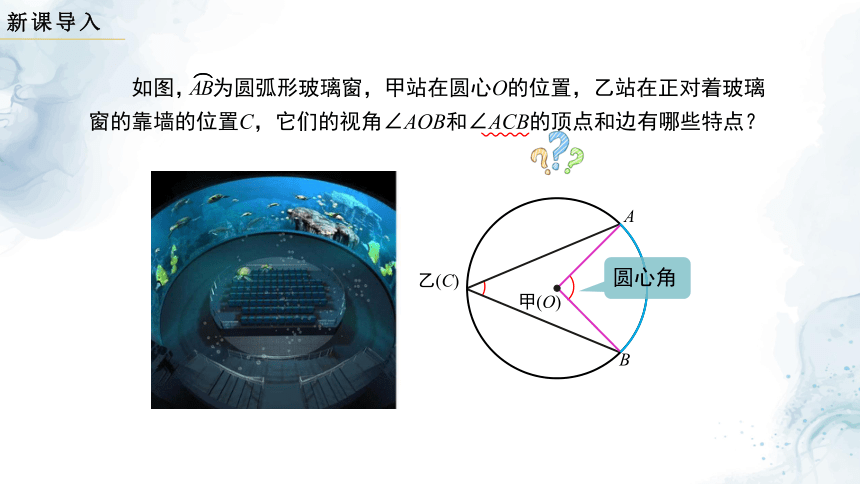
如图, 为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点?
A
B
甲(O)
乙(C)
圆心角
探索新知 知识点1 圆周角的定义
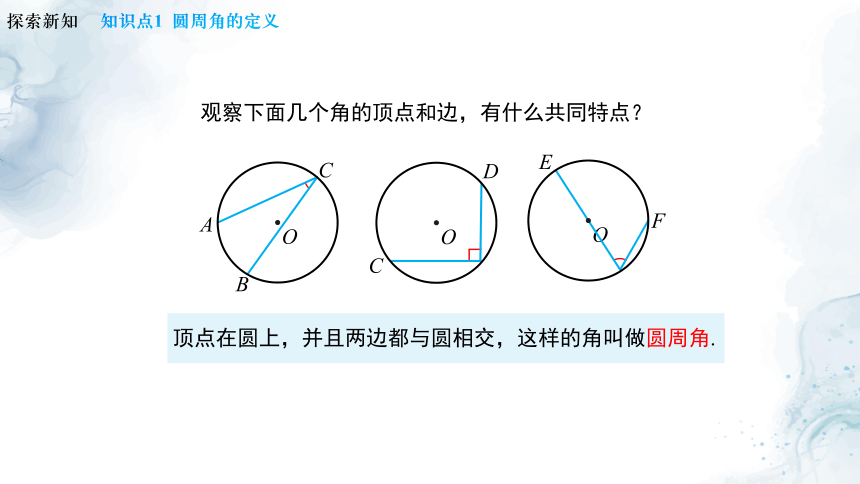
观察下面几个角的顶点和边,有什么共同特点?
O
A
B
O
C
D
O
E
F
顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角.
C
探索新知 知识点1 圆周角的定义
A
O
B
C
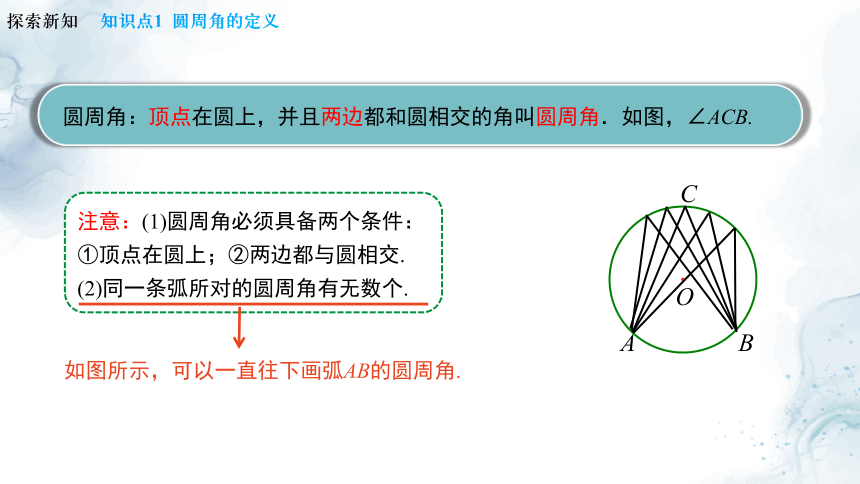
注意:(1)圆周角必须具备两个条件:
①顶点在圆上;②两边都与圆相交.
(2)同一条弧所对的圆周角有无数个.
如图所示,可以一直往下画弧AB的圆周角.
圆周角:顶点在圆上,并且两边都和圆相交的角叫圆周角.如图,∠ACB.
探索新知 知识点1 圆周角的定义
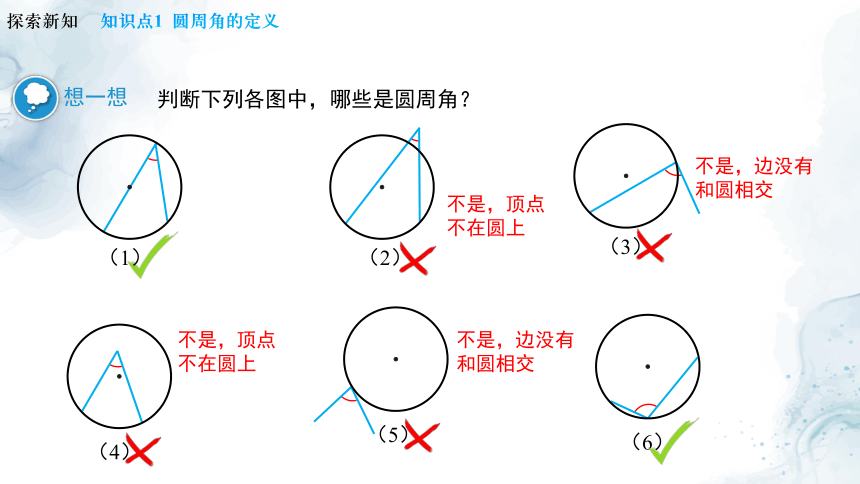
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
不是,顶点不在圆上
不是,边没有和圆相交
不是,顶点不在圆上
不是,边没有和圆相交
探索新知 知识点2 圆周角的定理及推论
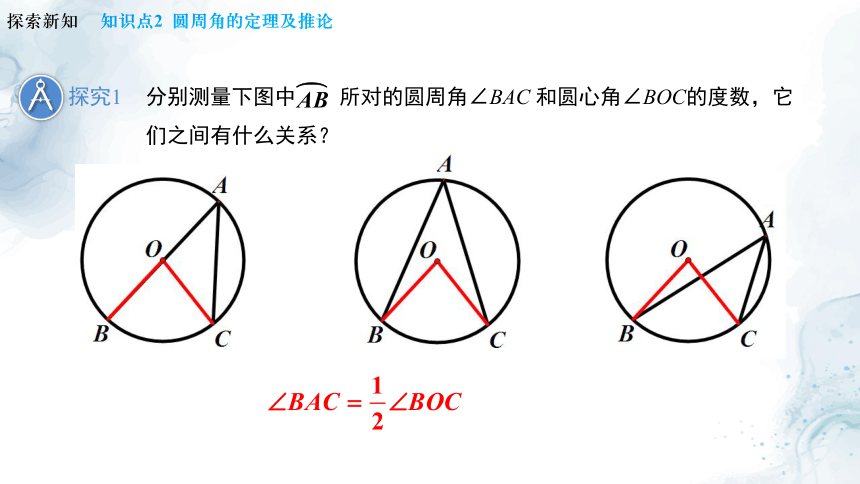
探究1
分别测量下图中 所对的圆周角∠BAC 和圆心角∠BOC的度数,它们之间有什么关系?
探索新知 知识点2 圆周角的定理及推论
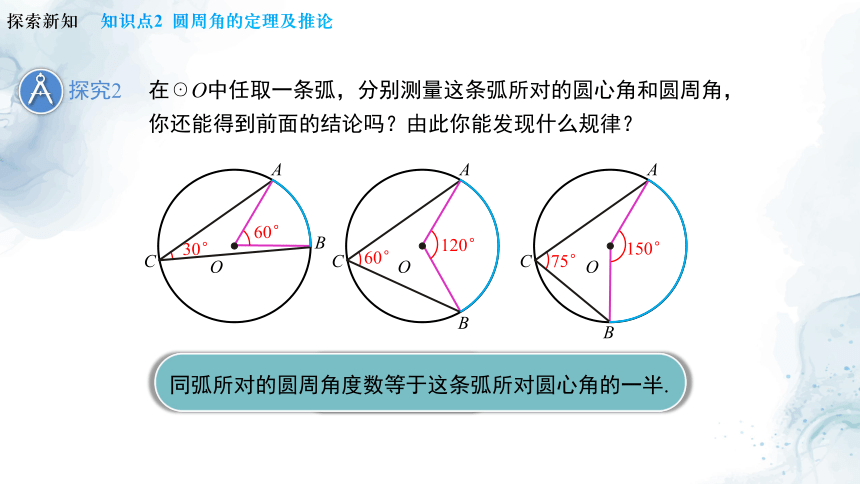
在☉O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?由此你能发现什么规律?
探究2
60°
30°
A
B
O
C
120°
60°
A
B
O
C
150°
75°
A
B
O
C
同弧所对的圆周角度数等于这条弧所对圆心角的一半.
探索新知 知识点2 圆周角的定理及推论
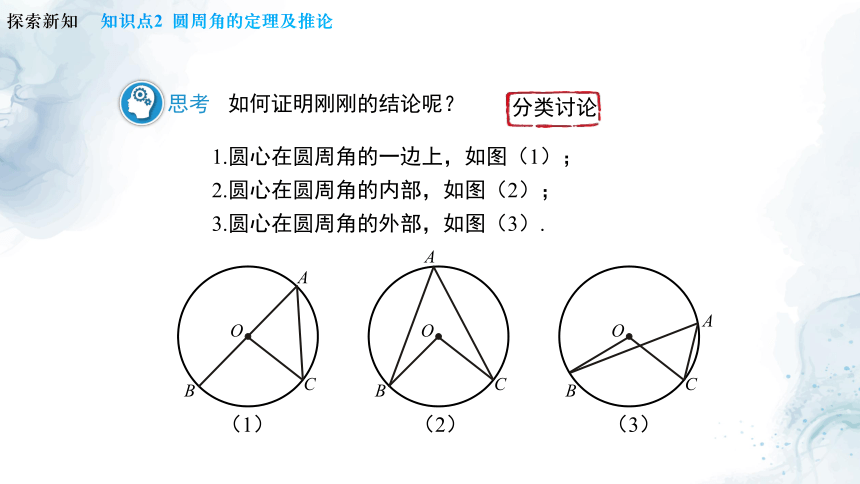
思考
如何证明刚刚的结论呢?
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
探索新知 知识点2 圆周角的定理及推论
证明
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
探索新知 知识点2 圆周角的定理及推论
圆心O在∠BAC的内部
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
探索新知 知识点2 圆周角的定理及推论
圆心O在∠BAC的外部
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
探索新知 知识点2 圆周角的定理及推论
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
探索新知 知识点2 圆周角的定理及推论
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
∠BAC ∠BDC ∠BEC
∠BAC ∠BDC ∠BEC
探索新知 知识点2 圆周角的定理及推论
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
推论1:同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
探索新知 知识点2 圆周角的定理及推论
如图,线段AB是☉O的直径,点C是☉O上的任意一点(除点A、B外),那么∠ACB就是直径AB所对的圆周角.想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵AB是直径,点O是圆心,
∴∠AOB180°.
∵∠ACB是直径AB所对的圆周角,
∴∠ACB ∠AOB=90°.
想一想:能不能直接运用圆周角定理解答?
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
在Rt△ABC中,
∴∠ACB∠ADB90°.
例1 如图,☉O直径AB为10cm,弦AC为6cm,∠ACB的平分线交☉O于D,求BC、AD、BD的长.
解:连接OD,∵AB是直径,
又∵CD平分∠ACB,∴∠ACD∠BCD
∴ADBD
A
O
B
D
C
·
6
10
在Rt△ABD中,AD2 BD2 AB2
∴ADBDAB 10
探索新知 知识点3 圆内接多边形
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 如,四边形ABCD是☉O的内接四边形,☉O是四边形ABCD的外接圆.五边形ABCDE是☉O的内接五边形,☉O是五边形ABCDE的外接圆.
探索新知 知识点3 圆内接多边形
思考
圆内接四边形的一组对角有什么关系?
O
A
C
B
D
连接OA,OC.
∵
又∵∠1 ∠2 360°
∴∠B ∠D 180°
猜想
互补
1
2
证明
同理:
∠A ∠C 180°
圆内接四边形的对角互补.
注意:每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
探索新知 知识点3 圆内接多边形
延伸
如图,四边形ABCD是⊙O的内接四边形;∠A与∠BCE有什么关系?
D
O
A
C
B
E
∠BCE ∠BCD 180°
∠BCD ∠A 180°
∠BCE ∠A
圆内接四边形的一个外角等于它的内对角.
当堂检测
Part Three
叁
B
A
C
B
130°
211
35°
课堂总结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆内接四边形的性质
一条弧所对的圆周角等于它所对的圆心角的一半.
圆内接四边形的对角互补.
1.顶点在圆上,
2.两边都与圆相交的角(二者必须同时具备)
圆周角定理
的推论
同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
THANKS
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
24.1.4圆周角
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
理解圆周角的概念,会叙述并证明圆周角定理
1
理解圆周角与圆心角的关系,并能运用圆周角定理解决简单的几何问题
2
理解掌握圆周角定理的推论及其证明过程和应用
3
理解并掌握圆内接四边形的概念和性质
4
探索新知
Part Two
贰
知识回顾
问题1:什么叫圆心角?指出图中的圆心角,并说说识别圆心角的需要注意什么?
顶点在圆心的角叫圆心角,∠BOC.
注意点:①顶点在圆心上②两条边和圆相交.
A
问题2:弧、弦、圆心角的关系定理是什么?
相等的圆心角所对的弧相等,所对的弦也相等.
相等的弧所对的圆心角相等,所对的弦也相等.
相等的弦所对的圆心角相等,所对的优弧和劣弧也相等.
新课导入
如图, 为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点?
A
B
甲(O)
乙(C)
圆心角
探索新知 知识点1 圆周角的定义
观察下面几个角的顶点和边,有什么共同特点?
O
A
B
O
C
D
O
E
F
顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角.
C
探索新知 知识点1 圆周角的定义
A
O
B
C
注意:(1)圆周角必须具备两个条件:
①顶点在圆上;②两边都与圆相交.
(2)同一条弧所对的圆周角有无数个.
如图所示,可以一直往下画弧AB的圆周角.
圆周角:顶点在圆上,并且两边都和圆相交的角叫圆周角.如图,∠ACB.
探索新知 知识点1 圆周角的定义
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
不是,顶点不在圆上
不是,边没有和圆相交
不是,顶点不在圆上
不是,边没有和圆相交
探索新知 知识点2 圆周角的定理及推论
探究1
分别测量下图中 所对的圆周角∠BAC 和圆心角∠BOC的度数,它们之间有什么关系?
探索新知 知识点2 圆周角的定理及推论
在☉O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?由此你能发现什么规律?
探究2
60°
30°
A
B
O
C
120°
60°
A
B
O
C
150°
75°
A
B
O
C
同弧所对的圆周角度数等于这条弧所对圆心角的一半.
探索新知 知识点2 圆周角的定理及推论
思考
如何证明刚刚的结论呢?
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
探索新知 知识点2 圆周角的定理及推论
证明
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
探索新知 知识点2 圆周角的定理及推论
圆心O在∠BAC的内部
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
探索新知 知识点2 圆周角的定理及推论
圆心O在∠BAC的外部
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
探索新知 知识点2 圆周角的定理及推论
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
探索新知 知识点2 圆周角的定理及推论
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
∠BAC ∠BDC ∠BEC
∠BAC ∠BDC ∠BEC
探索新知 知识点2 圆周角的定理及推论
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
推论1:同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
探索新知 知识点2 圆周角的定理及推论
如图,线段AB是☉O的直径,点C是☉O上的任意一点(除点A、B外),那么∠ACB就是直径AB所对的圆周角.想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵AB是直径,点O是圆心,
∴∠AOB180°.
∵∠ACB是直径AB所对的圆周角,
∴∠ACB ∠AOB=90°.
想一想:能不能直接运用圆周角定理解答?
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
在Rt△ABC中,
∴∠ACB∠ADB90°.
例1 如图,☉O直径AB为10cm,弦AC为6cm,∠ACB的平分线交☉O于D,求BC、AD、BD的长.
解:连接OD,∵AB是直径,
又∵CD平分∠ACB,∴∠ACD∠BCD
∴ADBD
A
O
B
D
C
·
6
10
在Rt△ABD中,AD2 BD2 AB2
∴ADBDAB 10
探索新知 知识点3 圆内接多边形
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 如,四边形ABCD是☉O的内接四边形,☉O是四边形ABCD的外接圆.五边形ABCDE是☉O的内接五边形,☉O是五边形ABCDE的外接圆.
探索新知 知识点3 圆内接多边形
思考
圆内接四边形的一组对角有什么关系?
O
A
C
B
D
连接OA,OC.
∵
又∵∠1 ∠2 360°
∴∠B ∠D 180°
猜想
互补
1
2
证明
同理:
∠A ∠C 180°
圆内接四边形的对角互补.
注意:每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
探索新知 知识点3 圆内接多边形
延伸
如图,四边形ABCD是⊙O的内接四边形;∠A与∠BCE有什么关系?
D
O
A
C
B
E
∠BCE ∠BCD 180°
∠BCD ∠A 180°
∠BCE ∠A
圆内接四边形的一个外角等于它的内对角.
当堂检测
Part Three
叁
B
A
C
B
130°
211
35°
课堂总结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆内接四边形的性质
一条弧所对的圆周角等于它所对的圆心角的一半.
圆内接四边形的对角互补.
1.顶点在圆上,
2.两边都与圆相交的角(二者必须同时具备)
圆周角定理
的推论
同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
THANKS
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
同课章节目录
