24.2.2直线和圆的位置关系(第1课时) 教学课件(共31张PPT)初中数学人教版(2012)九年级上册
文档属性
| 名称 | 24.2.2直线和圆的位置关系(第1课时) 教学课件(共31张PPT)初中数学人教版(2012)九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 14:33:42 | ||
图片预览











文档简介
(共31张PPT)
24.2.2直线和圆的位置关系(第1课时)
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
了解直线和圆的位置关系
1
理解直线和圆的三种位置关系中,圆心到直线的距离d和圆的半径r之间的数量关系
2
会运用直线和圆的三种位置关系的性质与判定进行有关计算
3
探索新知
Part Two
贰
新课导入
探索新知 知识点1 用定义判断直线与圆的位置关系
思考
如果我们把太阳看作一个圆,把地平线看作一条直线.太阳升起的过程中,太阳和地平线会有几种位置关系?
太阳与地平线有三种位置关系
思考
由此你能得出直线和圆有几种位置关系吗?
(地平线)
a(地平线)
●O
●O
●O
直线和圆有三种位置关系
探索新知 知识点1 用定义判断直线与圆的位置关系
思考
请在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
无公共点
1个公共点
2个公共点
无公共点
探索新知 知识点1 用定义判断直线与圆的位置关系
探索新知 知识点1 用定义判断直线与圆的位置关系
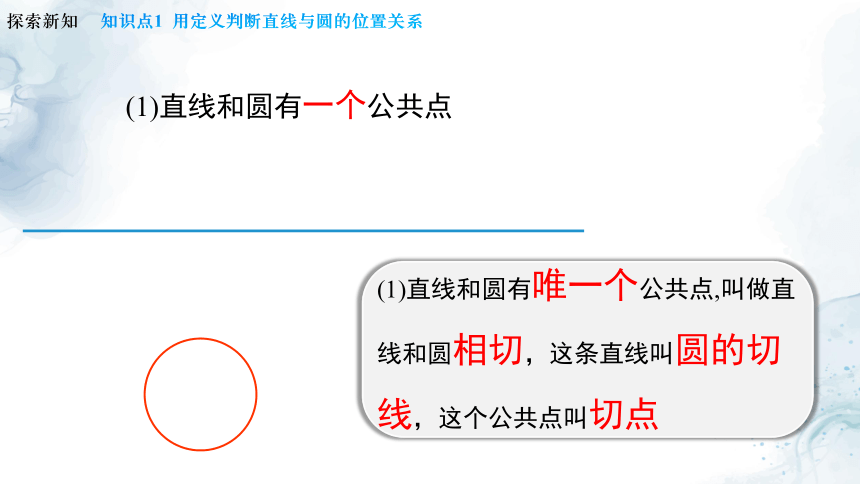
(1)直线和圆有一个公共点
(1)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点
探索新知 知识点1 用定义判断直线与圆的位置关系
(2)直线和圆有两个公共点.
(2)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点
探索新知 知识点1 用定义判断直线与圆的位置关系
(3)直线和圆没有公共点.
(3)直线和圆没有公共点时,叫做直线和圆相离
探索新知 知识点1 用定义判断直线与圆的位置关系
直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆没有公共点,这时我们说这条直线和圆相离.
割线
切线
切点
归纳
想一想
看图判断直线l与☉O的位置关系?
探索新知 知识点1 用定义判断直线与圆的位置关系
.O
.O
.O
.O
.O
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
判断正误:
做一做
探索新知 知识点1 用定义判断直线与圆的位置关系
①直线与圆最多有两个公共点;
②若C为⊙O上的一点,则过点C的直线与⊙O相切;
③若A,B是⊙O 外两点,则直线AB与⊙O相离;
④若C为⊙O内一点,则过点C的直线与⊙O相交.
探索新知 知识点2 用数量关系判断直线与圆的位置关系
思考
在纸上画一个圆,用直尺在圆上移动,观察一下,除了公共点的个数发生改变外,还有什么量在改变?
∟
∟
相交
o
o
o
相切
相离
∟
圆心到直线的距离在改变.
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
探索新知 知识点2 用数量关系判断直线与圆的位置关系
思考
设⊙O的半径为 r,圆心 O 到直线 l 的距离为 d. 在直线与圆的不同位置关系中,d 与 r 具有怎样的大小关系呢?
∟
∟
相交
o
∟
o
o
d < r
d = r
d > r
相切
相离
反过来,也成立吗?
d
d
d
r
r
r
归纳
直线和圆的位置关系
探索新知 知识点2 用数量关系判断直线与圆的位置关系
有2个公共点
直线与圆相交
d有1个公共点
无公共点
直线与圆相切
直线与圆相离
d=r
d>r
交点个数
位置关系
数量关系
数形结合
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
A
C
B
8
6
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
D
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
解:过C作CD⊥AB,垂足为D.
在△ABC中,
根据三角形的面积公式有
∴
即圆心 C 到AB的距离 d=4.8cm.
所以 (1)当r=4cm时,
有d >r,
因此⊙C和AB相离.
A
C
B
8
6
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
(2)当r=4.8cm时,有d=r.
因此⊙C和 AB 相切.
A
C
B
8
6
D
d
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
(3)当r=6cm时,有d因此,⊙C和AB相交.
A
C
B
8
6
D
d
当堂检测
Part Three
叁
C
相离
0<r<2
10s或6s
7
课堂总结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
dTHANKS
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
24.2.2直线和圆的位置关系(第1课时)
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
了解直线和圆的位置关系
1
理解直线和圆的三种位置关系中,圆心到直线的距离d和圆的半径r之间的数量关系
2
会运用直线和圆的三种位置关系的性质与判定进行有关计算
3
探索新知
Part Two
贰
新课导入
探索新知 知识点1 用定义判断直线与圆的位置关系
思考
如果我们把太阳看作一个圆,把地平线看作一条直线.太阳升起的过程中,太阳和地平线会有几种位置关系?
太阳与地平线有三种位置关系
思考
由此你能得出直线和圆有几种位置关系吗?
(地平线)
a(地平线)
●O
●O
●O
直线和圆有三种位置关系
探索新知 知识点1 用定义判断直线与圆的位置关系
思考
请在纸上画一条直线 l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
无公共点
1个公共点
2个公共点
无公共点
探索新知 知识点1 用定义判断直线与圆的位置关系
探索新知 知识点1 用定义判断直线与圆的位置关系
(1)直线和圆有一个公共点
(1)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点
探索新知 知识点1 用定义判断直线与圆的位置关系
(2)直线和圆有两个公共点.
(2)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点
探索新知 知识点1 用定义判断直线与圆的位置关系
(3)直线和圆没有公共点.
(3)直线和圆没有公共点时,叫做直线和圆相离
探索新知 知识点1 用定义判断直线与圆的位置关系
直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆没有公共点,这时我们说这条直线和圆相离.
割线
切线
切点
归纳
想一想
看图判断直线l与☉O的位置关系?
探索新知 知识点1 用定义判断直线与圆的位置关系
.O
.O
.O
.O
.O
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
判断正误:
做一做
探索新知 知识点1 用定义判断直线与圆的位置关系
①直线与圆最多有两个公共点;
②若C为⊙O上的一点,则过点C的直线与⊙O相切;
③若A,B是⊙O 外两点,则直线AB与⊙O相离;
④若C为⊙O内一点,则过点C的直线与⊙O相交.
探索新知 知识点2 用数量关系判断直线与圆的位置关系
思考
在纸上画一个圆,用直尺在圆上移动,观察一下,除了公共点的个数发生改变外,还有什么量在改变?
∟
∟
相交
o
o
o
相切
相离
∟
圆心到直线的距离在改变.
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
探索新知 知识点2 用数量关系判断直线与圆的位置关系
思考
设⊙O的半径为 r,圆心 O 到直线 l 的距离为 d. 在直线与圆的不同位置关系中,d 与 r 具有怎样的大小关系呢?
∟
∟
相交
o
∟
o
o
d < r
d = r
d > r
相切
相离
反过来,也成立吗?
d
d
d
r
r
r
归纳
直线和圆的位置关系
探索新知 知识点2 用数量关系判断直线与圆的位置关系
有2个公共点
直线与圆相交
d
无公共点
直线与圆相切
直线与圆相离
d=r
d>r
交点个数
位置关系
数量关系
数形结合
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
A
C
B
8
6
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
D
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
解:过C作CD⊥AB,垂足为D.
在△ABC中,
根据三角形的面积公式有
∴
即圆心 C 到AB的距离 d=4.8cm.
所以 (1)当r=4cm时,
有d >r,
因此⊙C和AB相离.
A
C
B
8
6
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
(2)当r=4.8cm时,有d=r.
因此⊙C和 AB 相切.
A
C
B
8
6
D
d
例 在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,AC=8cm,以C为圆心,AB与r为半径的圆⊙C的位置关系?
(1) r=4cm;(2) r=4.8cm; (3) r=6cm.
(3)当r=6cm时,有d
A
C
B
8
6
D
d
当堂检测
Part Three
叁
C
相离
0<r<2
10s或6s
7
课堂总结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
同课章节目录
