九年级数学上点拨与精练 第24章圆24.1.3 弧、弦、圆心角(含解析)
文档属性
| 名称 | 九年级数学上点拨与精练 第24章圆24.1.3 弧、弦、圆心角(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学上点拨与精练
第24章 圆
24.1.3 弧、弦、圆心角
学习目标:
理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的计算和证明;
在探索弧、弦、圆心角的关系的过程中,学会用转化的数学思想解决问题。
老师告诉你
同一圆中证明两弦相等的四个方法:
若两弦位于两个不同的三角形中,证明两弦所在的三角形全等;
若两弦位于同一三角形中,由“等角对等边”证明两弦相等;
证明两弦所对的弧相等;
证明两弦所对的圆心角相等。
一、知识点拨
知识点1.圆心角
圆心角:我们把顶点在圆心的角叫做圆心角。如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
注意:
(1)顶点在圆心的角,叫圆心角,如∠AOB .
(2)圆心角 ∠AOB 所对的弧为.
(3)圆心角 ∠AOB所对的弦为AB.
对于任意给定一个圆心角,都对应出现三个量:即圆心角、弧、弦。
【新知导学】
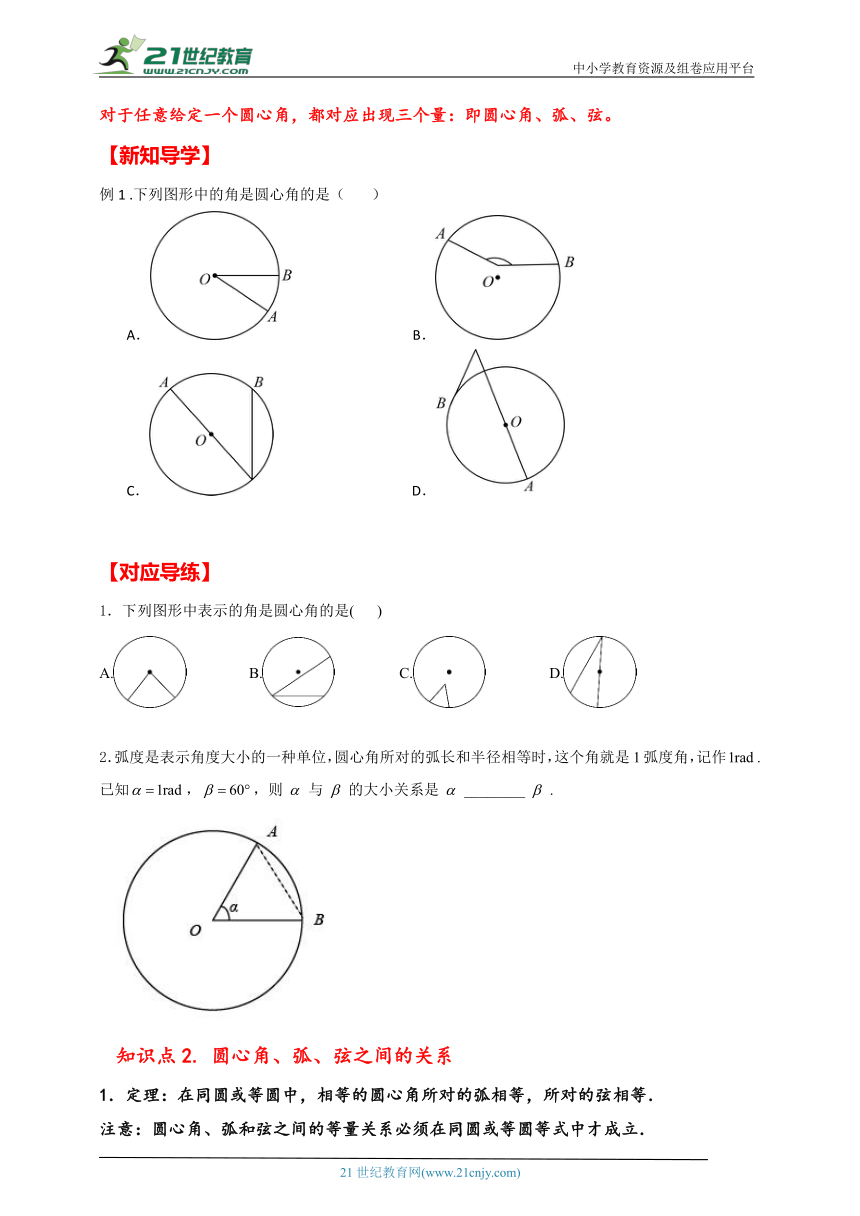
例1 .下列图形中的角是圆心角的是( )
A. B.
C. D.
【对应导练】
1.下列图形中表示的角是圆心角的是( )
A. B. C. D.
2.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,,则与的大小关系是________.
知识点2. 圆心角、弧、弦之间的关系
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
注意:圆心角、弧和弦之间的等量关系必须在同圆或等圆等式中才成立.
2.数学语言:如果①∠AOB=∠COD,那么有
【新知导学】
例2 .如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
(1)求证:;
(2)若的度数为70°,求∠C的度数.
【对应导练】
1.如图,在同圆中,若,则________.(“>”“<”或“=”)
2.如图,AB为的直径,C,D是上的两点,且.求证:.
3.如图,D,E分别是两条半径OA,OB的中点,
(1)求证:.
(2)若,四边形ODCE的面积为y,求y与x的函数关系式.
知识点3 相等的圆心角、弧、弦之间的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
具体表达就是:
(1)在同圆或等圆中,如果弧相等,那么弧所对的圆心角相等,弧所对的弦相等。
(2)在同圆或等圆中,如果弦相等,那么弦所对应的圆心角相等,弦所对应的优弧相等,弦所对应的劣弧相等。
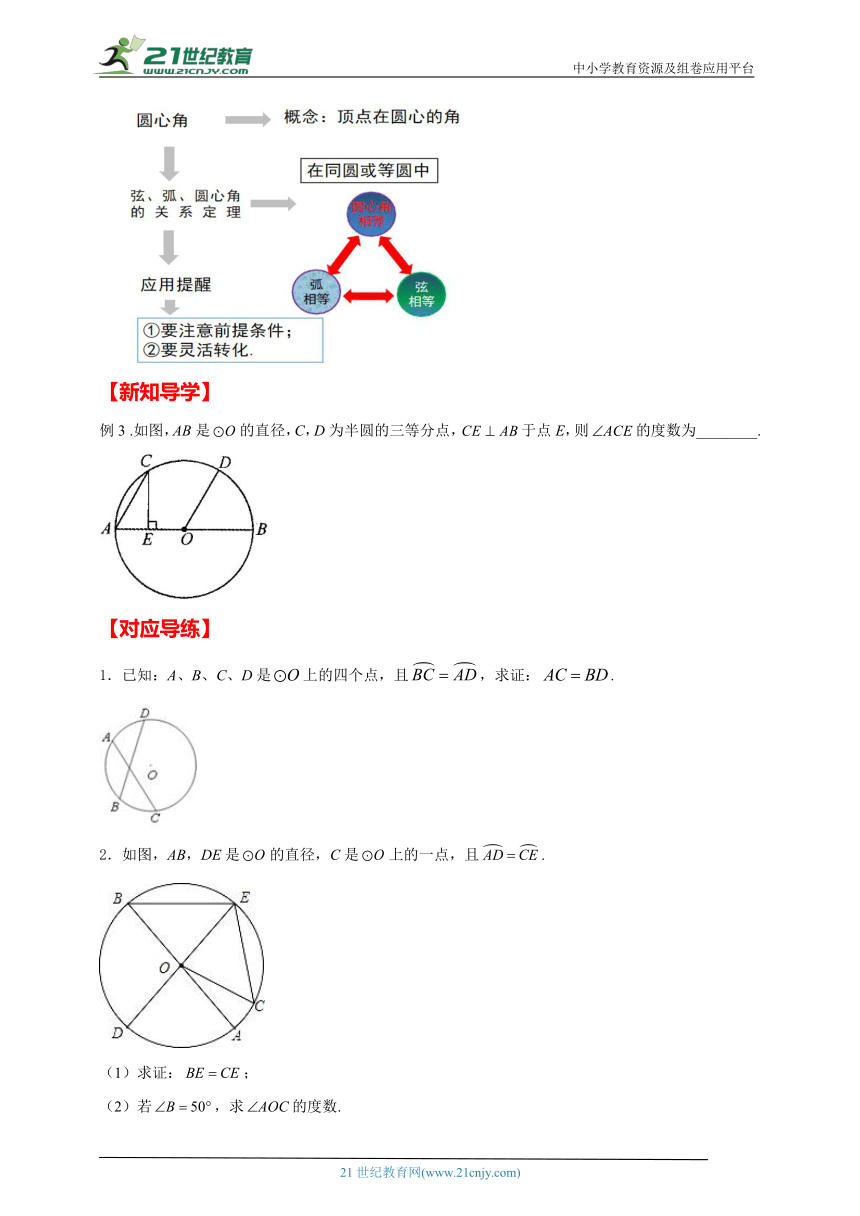
注意:理解弦、弧、圆心角的关系定理的思维图
【新知导学】
例3 .如图,AB是的直径,C,D为半圆的三等分点,于点E,则的度数为________.
【对应导练】
1.已知:A、B、C、D是上的四个点,且,求证:.
2.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
3.如图,的弦的延长线相交于点P,且.求证:.
4.如图,在中,于点D,于点E,求证:.
5.如图,BD是的直径,C是的中点,若,则的度数为___________.
题型训练
利用等弧对等圆心角证明线段相等
一、解答题
1.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
2.如图,在中,弦AB与CD相交于点E, ,连接AD,BC.
求证:(1);(2).
利用等弧对等圆心角证明线段平行
3.如图,AB是⊙O的直径,,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
利用等圆心角对等弧求角度
4.如图,是的直径,,,则的大小为______.
5.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
6.如图,为上的三等分点.
(1)求的度数;
(2)若,求的半径长及.
课堂达标
一、单选题(每小题4分,共32分)
1.下列图形中的角是圆心角的是( )
A. B. C. D.
2.下列说法正确的是( )
A.等弧所对的弦相等 B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等 D.相等的圆心角所对的弦相等
3.如图,在中﹐,,则( )
A. B. C. D.
4.下列关于圆的说法中,错误的是( )
A.半径、圆心角分别相等的两段弧一定是等弧
B.如果两条弦相等,那么这两条弦所对的圆心角相等
C.圆的对称轴是任意一条直径所在的直线
D.拱形不一定是弓形
5.如图,AB是的直径,已知,,那么的度数为( )
A.80° B.85° C.90° D.95°
6.如图,在中,,则以下数量关系正确的是( )
A. B. C. D.
7.如图,是的直径,点C在上,,D是的中点,则( )
A. B. C. D.
8.如图,是上的点,于点,于点,,则与的关系是( )
A. B. C. D.不能确定
二、填空题(每小题4分,共20分)
9.如图,在中,,A、C之间的距离为4,则线段________.
10.如图,C为弧AB的中点,于点N,于点M,cm,则__________cm.
11.一条弦把圆分为两部分,那么这条弦所对的圆周角的度数为___________.
12.如图,是的直径,是弦,点E是的中点,交于点D.连接.若,则的长为 .
13.如图,点在的边上,过三点的圆的圆心为点E,过三点的圆的圆心为点D.如果,那么 .
三、解答题(共6小题,共48分)
14.(8分)如图,中,弦AB与CD相交于点E,,连接AD,BC.
求证:(1);
(2).
15.(7分)如图,以等边三角形的边为直径作交于点,交于点,判断,,之间的大小关系,并说明理由.
16.(7分)如图,已知AB是的直径,M,N分别是AO,BO的中点,.
求证:.
17.(8分)如图,在中,,于点D.求证:.
18.(9分)如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
19.(9分)如图,AB是的直径,P,C是上的点,,弦PC交AB于点D,连接OC.
(1)求证:.
(2)若,求的度数.
九年级数学上点拨与精练
第24章 圆
24.1.3 弧、弦、圆心角
学习目标:
理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的计算和证明;
在探索弧、弦、圆心角的关系的过程中,学会用转化的数学思想解决问题。
老师告诉你
同一圆中证明两弦相等的四个方法:
若两弦位于两个不同的三角形中,证明两弦所在的三角形全等;
若两弦位于同一三角形中,由“等角对等边”证明两弦相等;
证明两弦所对的弧相等;
证明两弦所对的圆心角相等。
一、知识点拨
知识点1.圆心角
圆心角:我们把顶点在圆心的角叫做圆心角。如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
注意:
(1)顶点在圆心的角,叫圆心角,如∠AOB .
(2)圆心角 ∠AOB 所对的弧为.
(3)圆心角 ∠AOB所对的弦为AB.
对于任意给定一个圆心角,都对应出现三个量:即圆心角、弧、弦。
【新知导学】
例1 .下列图形中的角是圆心角的是( )
A. B.
C. D.
【答案】A
【分析】根据圆心角的定义作答即可.
【详解】解:圆心角的定义:圆心角的顶点必在圆心上,
所以选项A符合题意,选项B,C,D不合题意.
故选:A.
【点睛】本题考查的是圆心角的定义,正确掌握圆心角的定义是解题的关键.
【对应导练】
1.下列图形中表示的角是圆心角的是( )
A. B. C. D.
答案:A
解析:根据圆心角的定义:顶点在圆心的角是圆心角可知,B,C,D项图形中的顶点都不在圆心上,所以它们都不是圆心角.
故选A.
2.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,,则与的大小关系是________.
答案:<
解析:解:根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作1rad,当时,易知三角形为等边三角形,弦长等于半径,圆心角所对的弧长比半径大,,故答案是:<.
知识点2. 圆心角、弧、弦之间的关系
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
注意:圆心角、弧和弦之间的等量关系必须在同圆或等圆等式中才成立.
2.数学语言:如果①∠AOB=∠COD,那么有
【新知导学】
例2 .如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
(1)求证:;
(2)若的度数为70°,求∠C的度数.
【分析】(1)要证明,则要证明∠DAF=∠GAD,由题干条件能够证明之;
(2)根据的度数为70°,得到∠BAF=70°,于是得到∠B=∠AFB(180°﹣∠BAF)=55°,根据平行四边形的性质即可得到结论.
【解答】(1)证明:连接AF.
∵A为圆心,∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴;
(2)解:∵的度数为70°,
∴∠BAF=70°,
∵AB=AF,
∴∠B=∠AFB(180°﹣∠BAF)=55°,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠C=180°﹣∠B=125°.
【点评】本题考查了平行四边形性质,平行线性质,等知识点的应用,关键是求出∠DAF=∠GAD,题目比较典型,难度不大.
【对应导练】
1.如图,在同圆中,若,则________.(“>”“<”或“=”)
答案:<
解析:取的中点E,连接,,,,,
,
,
,
,
在中,,
.
故答案为:<.
2.如图,AB为的直径,C,D是上的两点,且.求证:.
答案:证明:,
.
,
,
,
.
3.如图,D,E分别是两条半径OA,OB的中点,
(1)求证:.
(2)若,四边形ODCE的面积为y,求y与x的函数关系式.
答案:(1)如答图,连接OC.
,
.
D,E分别是两条半径OA,OB的中点,
.
在和中,
,
.
(2)如答图,连接AC.
.
又,
为等边三角形.
D是OA的中点,,
.
在中,,
四边形ODCE的面积为.
故y与x的函数关系式为.
知识点3 相等的圆心角、弧、弦之间的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
具体表达就是:
(1)在同圆或等圆中,如果弧相等,那么弧所对的圆心角相等,弧所对的弦相等。
(2)在同圆或等圆中,如果弦相等,那么弦所对应的圆心角相等,弦所对应的优弧相等,弦所对应的劣弧相等。
注意:理解弦、弧、圆心角的关系定理的思维图
【新知导学】
例3 .如图,AB是的直径,C,D为半圆的三等分点,于点E,则的度数为________.
答案:30°
解析:连接OC.AB是直径,,,,是等边三角形,,,,.
【对应导练】
1.已知:A、B、C、D是上的四个点,且,求证:.
答案:详见解析
解析:证明:
.
2.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
答案:(1)证明:,
.
,
,
;
(2)解:,,
.
由(1)知,,
,
.
解析:
3.如图,的弦的延长线相交于点P,且.求证:.
答案:连接,
,
,
,即,
,
4.如图,在中,于点D,于点E,求证:.
答案:证明:如图,连接.
于点D,于点E,
在与中,,
.
又.
5.如图,BD是的直径,C是的中点,若,则的度数为___________.
答案:
解析:C是的中点,,.是的直径,..
题型训练
利用等弧对等圆心角证明线段相等
2024年10月21日xx学校初中数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
解析:
2.如图,在中,弦AB与CD相交于点E, ,连接AD,BC.
求证:(1);(2).
答案:(1),
,,
.
(2),.
又,,
,
.
解析:
利用等弧对等圆心角证明线段平行
3.如图,AB是⊙O的直径,,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
【分析】(1)由等弧所对的圆心角相等推知∠1=∠COD=60°;然后根据圆上的点到圆心的距离都等于圆的半径知OA=OC,从而证得△AOC是等边三角形;
(2)证法一:利用同垂直于一条直线的两条直线互相平行来证明OC∥BD;证法二:通过证明同位角∠1=∠B,推知OC∥BD.
【解答】解:(1)△AOC是等边三角形,
证明:∵,
∴∠1=∠COD=60°,
∵OA=OC(⊙O的半径),
∴△AOC是等边三角形;
(2)证法一:∵,
∴OC⊥AD,
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD,
∴OC∥BD;
证法二:∵,
∴∠1=∠COD∠AOD,
又∠B∠AOD,
∴∠1=∠B,
∴OC∥BD.
【点评】本题综合考查了圆周角定理、等边三角形的判定以及平行线的判定.在证明△AOC是等边三角形时,利用了等边三角形的内角是60°的性质.
利用等圆心角对等弧求角度
4.如图,是的直径,,,则的大小为______.
答案:/度
解析:∵是的直径,,,
∴,
∴,
故答案为:.
5.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
答案:(1)证明:,
.
,
,
;
(2)解:,,
.
由(1)知,,
,
.
解析:
6.如图,为上的三等分点.
(1)求的度数;
(2)若,求的半径长及.
答案:(1)为上的三等分点
的度数为:.
(2)过点O作于点D
为上的三等分点
即是等边三角形,且
则,
故
课堂达标
一、单选题(每小题4分,共32分)
1.下列图形中的角是圆心角的是( )
A. B. C. D.
答案:A
解析:圆心角的定义:圆心角的顶点必在圆心上,
所以选项A符合题意,选项B,C,D不合题意.
故选:A.
2.下列说法正确的是( )
A.等弧所对的弦相等 B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等 D.相等的圆心角所对的弦相等
答案:A
解析:A、等弧所对的弦一定相等;故原说法正确;
B、在同圆和等圆中,相等的弦所对的弧相等,故原说法错误;
C、在同圆和等圆中,相等的圆心角所对的弧相等,故原说法错误;
D、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.故原说法错误;
故选:A.
3.如图,在中﹐,,则( )
A. B. C. D.
答案:B
解析:,
.
故选:B.
4.下列关于圆的说法中,错误的是( )
A.半径、圆心角分别相等的两段弧一定是等弧
B.如果两条弦相等,那么这两条弦所对的圆心角相等
C.圆的对称轴是任意一条直径所在的直线
D.拱形不一定是弓形
答案:B
解析:A.半径、圆心角分别相等的两段弧一定是等弧,所以A选项不符合题意;
B.在同圆或等圆中,如果两条弦相等,那么这两条弦所对的圆心角相等,所以B选项符合题意;
C.圆的对称轴是任意一条直径所在的直线,所以C选项不符合题意;
D.拱形加上跨度为弓形,所以D选项不符合题意.
故选:B.
5.如图,AB是的直径,已知,,那么的度数为( )
A.80° B.85° C.90° D.95°
答案:C
解析:,,
,,
,
;
故选C.
6.如图,在中,,则以下数量关系正确的是( )
A. B. C. D.
答案:C
解析:如答图,连接BC...故选C.
7.如图,是的直径,点C在上,,D是的中点,则( )
A. B. C. D.
答案:C
解析:如图,连接.
是的直径,,.
是的中点,
.
.
8.如图,是上的点,于点,于点,,则与的关系是( )
A. B. C. D.不能确定
答案:A
解析:,又,,,.故选A.
二、填空题(每小题4分,共20分)
9.如图,在中,,A、C之间的距离为4,则线段________.
答案:4
解析:如图,连接BD,AC.
,
,
,
故答案为4.
10.如图,C为弧AB的中点,于点N,于点M,cm,则__________cm.
答案:2
解析:连接OC,根据圆心角、弧、弦之间的关系求出,
根据角平分线性质得出,
根据垂径定理得出cm,
于是cm.
11.一条弦把圆分为两部分,那么这条弦所对的圆周角的度数为___________.
答案:或
解析:如图,
连接.弦将分为两部分,
则;
∴,;
故这条弦所对的圆周角的度数为或.
12.如图,是的直径,是弦,点E是的中点,交于点D.连接.若,则的长为 .
答案:8
解析:连接,如图所示
点E是的中点,
,
设的半径为r,则
,即
,
,解得.
,.
13.如图,点在的边上,过三点的圆的圆心为点E,过三点的圆的圆心为点D.如果,那么 .
答案:
解析:连接,如图,设
而,
,
即得,故答案为.
三、解答题(共6小题,共48分)
14.(8分)如图,中,弦AB与CD相交于点E,,连接AD,BC.
求证:(1);
(2).
答案:(1)见解析
(2)见解析
解析:(1),
,即,
;
(2),
,
又,,
,
.
15.(7分)如图,以等边三角形的边为直径作交于点,交于点,判断,,之间的大小关系,并说明理由.
答案:.理由如下:
如图,连接,
为等边三角形,,
又,
与都是等边三角形,
,
,
,
.
16.(7分)如图,已知AB是的直径,M,N分别是AO,BO的中点,.
求证:.
答案:证明:连接OC,OD.
M,N分别是AO,BO的中点,
,且.
又,.
.
解析:
17.(8分)如图,在中,,于点D.求证:.
答案:证明:延长AD交于点E,
,
,,
,
,
,
.
18.(9分)如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
19.(9分)如图,AB是的直径,P,C是上的点,,弦PC交AB于点D,连接OC.
(1)求证:.
(2)若,求的度数.
答案:(1)证明:如答图,连接OP.
.
在和中,
,
.
(2)设,则.
.
,
.
在中,,解得.
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上点拨与精练
第24章 圆
24.1.3 弧、弦、圆心角
学习目标:
理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的计算和证明;
在探索弧、弦、圆心角的关系的过程中,学会用转化的数学思想解决问题。
老师告诉你
同一圆中证明两弦相等的四个方法:
若两弦位于两个不同的三角形中,证明两弦所在的三角形全等;
若两弦位于同一三角形中,由“等角对等边”证明两弦相等;
证明两弦所对的弧相等;
证明两弦所对的圆心角相等。
一、知识点拨
知识点1.圆心角
圆心角:我们把顶点在圆心的角叫做圆心角。如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
注意:
(1)顶点在圆心的角,叫圆心角,如∠AOB .
(2)圆心角 ∠AOB 所对的弧为.
(3)圆心角 ∠AOB所对的弦为AB.
对于任意给定一个圆心角,都对应出现三个量:即圆心角、弧、弦。
【新知导学】
例1 .下列图形中的角是圆心角的是( )
A. B.
C. D.
【对应导练】
1.下列图形中表示的角是圆心角的是( )
A. B. C. D.
2.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,,则与的大小关系是________.
知识点2. 圆心角、弧、弦之间的关系
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
注意:圆心角、弧和弦之间的等量关系必须在同圆或等圆等式中才成立.
2.数学语言:如果①∠AOB=∠COD,那么有
【新知导学】
例2 .如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
(1)求证:;
(2)若的度数为70°,求∠C的度数.
【对应导练】
1.如图,在同圆中,若,则________.(“>”“<”或“=”)
2.如图,AB为的直径,C,D是上的两点,且.求证:.
3.如图,D,E分别是两条半径OA,OB的中点,
(1)求证:.
(2)若,四边形ODCE的面积为y,求y与x的函数关系式.
知识点3 相等的圆心角、弧、弦之间的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
具体表达就是:
(1)在同圆或等圆中,如果弧相等,那么弧所对的圆心角相等,弧所对的弦相等。
(2)在同圆或等圆中,如果弦相等,那么弦所对应的圆心角相等,弦所对应的优弧相等,弦所对应的劣弧相等。
注意:理解弦、弧、圆心角的关系定理的思维图
【新知导学】
例3 .如图,AB是的直径,C,D为半圆的三等分点,于点E,则的度数为________.
【对应导练】
1.已知:A、B、C、D是上的四个点,且,求证:.
2.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
3.如图,的弦的延长线相交于点P,且.求证:.
4.如图,在中,于点D,于点E,求证:.
5.如图,BD是的直径,C是的中点,若,则的度数为___________.
题型训练
利用等弧对等圆心角证明线段相等
一、解答题
1.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
2.如图,在中,弦AB与CD相交于点E, ,连接AD,BC.
求证:(1);(2).
利用等弧对等圆心角证明线段平行
3.如图,AB是⊙O的直径,,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
利用等圆心角对等弧求角度
4.如图,是的直径,,,则的大小为______.
5.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
6.如图,为上的三等分点.
(1)求的度数;
(2)若,求的半径长及.
课堂达标
一、单选题(每小题4分,共32分)
1.下列图形中的角是圆心角的是( )
A. B. C. D.
2.下列说法正确的是( )
A.等弧所对的弦相等 B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等 D.相等的圆心角所对的弦相等
3.如图,在中﹐,,则( )
A. B. C. D.
4.下列关于圆的说法中,错误的是( )
A.半径、圆心角分别相等的两段弧一定是等弧
B.如果两条弦相等,那么这两条弦所对的圆心角相等
C.圆的对称轴是任意一条直径所在的直线
D.拱形不一定是弓形
5.如图,AB是的直径,已知,,那么的度数为( )
A.80° B.85° C.90° D.95°
6.如图,在中,,则以下数量关系正确的是( )
A. B. C. D.
7.如图,是的直径,点C在上,,D是的中点,则( )
A. B. C. D.
8.如图,是上的点,于点,于点,,则与的关系是( )
A. B. C. D.不能确定
二、填空题(每小题4分,共20分)
9.如图,在中,,A、C之间的距离为4,则线段________.
10.如图,C为弧AB的中点,于点N,于点M,cm,则__________cm.
11.一条弦把圆分为两部分,那么这条弦所对的圆周角的度数为___________.
12.如图,是的直径,是弦,点E是的中点,交于点D.连接.若,则的长为 .
13.如图,点在的边上,过三点的圆的圆心为点E,过三点的圆的圆心为点D.如果,那么 .
三、解答题(共6小题,共48分)
14.(8分)如图,中,弦AB与CD相交于点E,,连接AD,BC.
求证:(1);
(2).
15.(7分)如图,以等边三角形的边为直径作交于点,交于点,判断,,之间的大小关系,并说明理由.
16.(7分)如图,已知AB是的直径,M,N分别是AO,BO的中点,.
求证:.
17.(8分)如图,在中,,于点D.求证:.
18.(9分)如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
19.(9分)如图,AB是的直径,P,C是上的点,,弦PC交AB于点D,连接OC.
(1)求证:.
(2)若,求的度数.
九年级数学上点拨与精练
第24章 圆
24.1.3 弧、弦、圆心角
学习目标:
理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的计算和证明;
在探索弧、弦、圆心角的关系的过程中,学会用转化的数学思想解决问题。
老师告诉你
同一圆中证明两弦相等的四个方法:
若两弦位于两个不同的三角形中,证明两弦所在的三角形全等;
若两弦位于同一三角形中,由“等角对等边”证明两弦相等;
证明两弦所对的弧相等;
证明两弦所对的圆心角相等。
一、知识点拨
知识点1.圆心角
圆心角:我们把顶点在圆心的角叫做圆心角。如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
注意:
(1)顶点在圆心的角,叫圆心角,如∠AOB .
(2)圆心角 ∠AOB 所对的弧为.
(3)圆心角 ∠AOB所对的弦为AB.
对于任意给定一个圆心角,都对应出现三个量:即圆心角、弧、弦。
【新知导学】
例1 .下列图形中的角是圆心角的是( )
A. B.
C. D.
【答案】A
【分析】根据圆心角的定义作答即可.
【详解】解:圆心角的定义:圆心角的顶点必在圆心上,
所以选项A符合题意,选项B,C,D不合题意.
故选:A.
【点睛】本题考查的是圆心角的定义,正确掌握圆心角的定义是解题的关键.
【对应导练】
1.下列图形中表示的角是圆心角的是( )
A. B. C. D.
答案:A
解析:根据圆心角的定义:顶点在圆心的角是圆心角可知,B,C,D项图形中的顶点都不在圆心上,所以它们都不是圆心角.
故选A.
2.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,,则与的大小关系是________.
答案:<
解析:解:根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作1rad,当时,易知三角形为等边三角形,弦长等于半径,圆心角所对的弧长比半径大,,故答案是:<.
知识点2. 圆心角、弧、弦之间的关系
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
注意:圆心角、弧和弦之间的等量关系必须在同圆或等圆等式中才成立.
2.数学语言:如果①∠AOB=∠COD,那么有
【新知导学】
例2 .如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
(1)求证:;
(2)若的度数为70°,求∠C的度数.
【分析】(1)要证明,则要证明∠DAF=∠GAD,由题干条件能够证明之;
(2)根据的度数为70°,得到∠BAF=70°,于是得到∠B=∠AFB(180°﹣∠BAF)=55°,根据平行四边形的性质即可得到结论.
【解答】(1)证明:连接AF.
∵A为圆心,∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴;
(2)解:∵的度数为70°,
∴∠BAF=70°,
∵AB=AF,
∴∠B=∠AFB(180°﹣∠BAF)=55°,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠C=180°﹣∠B=125°.
【点评】本题考查了平行四边形性质,平行线性质,等知识点的应用,关键是求出∠DAF=∠GAD,题目比较典型,难度不大.
【对应导练】
1.如图,在同圆中,若,则________.(“>”“<”或“=”)
答案:<
解析:取的中点E,连接,,,,,
,
,
,
,
在中,,
.
故答案为:<.
2.如图,AB为的直径,C,D是上的两点,且.求证:.
答案:证明:,
.
,
,
,
.
3.如图,D,E分别是两条半径OA,OB的中点,
(1)求证:.
(2)若,四边形ODCE的面积为y,求y与x的函数关系式.
答案:(1)如答图,连接OC.
,
.
D,E分别是两条半径OA,OB的中点,
.
在和中,
,
.
(2)如答图,连接AC.
.
又,
为等边三角形.
D是OA的中点,,
.
在中,,
四边形ODCE的面积为.
故y与x的函数关系式为.
知识点3 相等的圆心角、弧、弦之间的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
具体表达就是:
(1)在同圆或等圆中,如果弧相等,那么弧所对的圆心角相等,弧所对的弦相等。
(2)在同圆或等圆中,如果弦相等,那么弦所对应的圆心角相等,弦所对应的优弧相等,弦所对应的劣弧相等。
注意:理解弦、弧、圆心角的关系定理的思维图
【新知导学】
例3 .如图,AB是的直径,C,D为半圆的三等分点,于点E,则的度数为________.
答案:30°
解析:连接OC.AB是直径,,,,是等边三角形,,,,.
【对应导练】
1.已知:A、B、C、D是上的四个点,且,求证:.
答案:详见解析
解析:证明:
.
2.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
答案:(1)证明:,
.
,
,
;
(2)解:,,
.
由(1)知,,
,
.
解析:
3.如图,的弦的延长线相交于点P,且.求证:.
答案:连接,
,
,
,即,
,
4.如图,在中,于点D,于点E,求证:.
答案:证明:如图,连接.
于点D,于点E,
在与中,,
.
又.
5.如图,BD是的直径,C是的中点,若,则的度数为___________.
答案:
解析:C是的中点,,.是的直径,..
题型训练
利用等弧对等圆心角证明线段相等
2024年10月21日xx学校初中数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
解析:
2.如图,在中,弦AB与CD相交于点E, ,连接AD,BC.
求证:(1);(2).
答案:(1),
,,
.
(2),.
又,,
,
.
解析:
利用等弧对等圆心角证明线段平行
3.如图,AB是⊙O的直径,,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
【分析】(1)由等弧所对的圆心角相等推知∠1=∠COD=60°;然后根据圆上的点到圆心的距离都等于圆的半径知OA=OC,从而证得△AOC是等边三角形;
(2)证法一:利用同垂直于一条直线的两条直线互相平行来证明OC∥BD;证法二:通过证明同位角∠1=∠B,推知OC∥BD.
【解答】解:(1)△AOC是等边三角形,
证明:∵,
∴∠1=∠COD=60°,
∵OA=OC(⊙O的半径),
∴△AOC是等边三角形;
(2)证法一:∵,
∴OC⊥AD,
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD,
∴OC∥BD;
证法二:∵,
∴∠1=∠COD∠AOD,
又∠B∠AOD,
∴∠1=∠B,
∴OC∥BD.
【点评】本题综合考查了圆周角定理、等边三角形的判定以及平行线的判定.在证明△AOC是等边三角形时,利用了等边三角形的内角是60°的性质.
利用等圆心角对等弧求角度
4.如图,是的直径,,,则的大小为______.
答案:/度
解析:∵是的直径,,,
∴,
∴,
故答案为:.
5.如图,AB,DE是的直径,C是上的一点,且.
(1)求证:;
(2)若,求的度数.
答案:(1)证明:,
.
,
,
;
(2)解:,,
.
由(1)知,,
,
.
解析:
6.如图,为上的三等分点.
(1)求的度数;
(2)若,求的半径长及.
答案:(1)为上的三等分点
的度数为:.
(2)过点O作于点D
为上的三等分点
即是等边三角形,且
则,
故
课堂达标
一、单选题(每小题4分,共32分)
1.下列图形中的角是圆心角的是( )
A. B. C. D.
答案:A
解析:圆心角的定义:圆心角的顶点必在圆心上,
所以选项A符合题意,选项B,C,D不合题意.
故选:A.
2.下列说法正确的是( )
A.等弧所对的弦相等 B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等 D.相等的圆心角所对的弦相等
答案:A
解析:A、等弧所对的弦一定相等;故原说法正确;
B、在同圆和等圆中,相等的弦所对的弧相等,故原说法错误;
C、在同圆和等圆中,相等的圆心角所对的弧相等,故原说法错误;
D、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.故原说法错误;
故选:A.
3.如图,在中﹐,,则( )
A. B. C. D.
答案:B
解析:,
.
故选:B.
4.下列关于圆的说法中,错误的是( )
A.半径、圆心角分别相等的两段弧一定是等弧
B.如果两条弦相等,那么这两条弦所对的圆心角相等
C.圆的对称轴是任意一条直径所在的直线
D.拱形不一定是弓形
答案:B
解析:A.半径、圆心角分别相等的两段弧一定是等弧,所以A选项不符合题意;
B.在同圆或等圆中,如果两条弦相等,那么这两条弦所对的圆心角相等,所以B选项符合题意;
C.圆的对称轴是任意一条直径所在的直线,所以C选项不符合题意;
D.拱形加上跨度为弓形,所以D选项不符合题意.
故选:B.
5.如图,AB是的直径,已知,,那么的度数为( )
A.80° B.85° C.90° D.95°
答案:C
解析:,,
,,
,
;
故选C.
6.如图,在中,,则以下数量关系正确的是( )
A. B. C. D.
答案:C
解析:如答图,连接BC...故选C.
7.如图,是的直径,点C在上,,D是的中点,则( )
A. B. C. D.
答案:C
解析:如图,连接.
是的直径,,.
是的中点,
.
.
8.如图,是上的点,于点,于点,,则与的关系是( )
A. B. C. D.不能确定
答案:A
解析:,又,,,.故选A.
二、填空题(每小题4分,共20分)
9.如图,在中,,A、C之间的距离为4,则线段________.
答案:4
解析:如图,连接BD,AC.
,
,
,
故答案为4.
10.如图,C为弧AB的中点,于点N,于点M,cm,则__________cm.
答案:2
解析:连接OC,根据圆心角、弧、弦之间的关系求出,
根据角平分线性质得出,
根据垂径定理得出cm,
于是cm.
11.一条弦把圆分为两部分,那么这条弦所对的圆周角的度数为___________.
答案:或
解析:如图,
连接.弦将分为两部分,
则;
∴,;
故这条弦所对的圆周角的度数为或.
12.如图,是的直径,是弦,点E是的中点,交于点D.连接.若,则的长为 .
答案:8
解析:连接,如图所示
点E是的中点,
,
设的半径为r,则
,即
,
,解得.
,.
13.如图,点在的边上,过三点的圆的圆心为点E,过三点的圆的圆心为点D.如果,那么 .
答案:
解析:连接,如图,设
而,
,
即得,故答案为.
三、解答题(共6小题,共48分)
14.(8分)如图,中,弦AB与CD相交于点E,,连接AD,BC.
求证:(1);
(2).
答案:(1)见解析
(2)见解析
解析:(1),
,即,
;
(2),
,
又,,
,
.
15.(7分)如图,以等边三角形的边为直径作交于点,交于点,判断,,之间的大小关系,并说明理由.
答案:.理由如下:
如图,连接,
为等边三角形,,
又,
与都是等边三角形,
,
,
,
.
16.(7分)如图,已知AB是的直径,M,N分别是AO,BO的中点,.
求证:.
答案:证明:连接OC,OD.
M,N分别是AO,BO的中点,
,且.
又,.
.
解析:
17.(8分)如图,在中,,于点D.求证:.
答案:证明:延长AD交于点E,
,
,,
,
,
,
.
18.(9分)如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
19.(9分)如图,AB是的直径,P,C是上的点,,弦PC交AB于点D,连接OC.
(1)求证:.
(2)若,求的度数.
答案:(1)证明:如答图,连接OP.
.
在和中,
,
.
(2)设,则.
.
,
.
在中,,解得.
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
