九年级数学上点拨与精练 第24章圆24.1专题 构造圆的基本性质的基本图形的常用辅助线(含解析)
文档属性
| 名称 | 九年级数学上点拨与精练 第24章圆24.1专题 构造圆的基本性质的基本图形的常用辅助线(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-27 19:53:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学上点拨与精练
第24章 圆
24.1 专题 构造圆的基本性质的基本图形的常用辅助线
老师告诉你
用圆的有关性质解题的常用方法是将圆的有关问题转化为三角形问题求解,解题时需要根据图形的特征,作出相对应的辅助线,在图形中构造等腰三角形、直角三角形、全等三角形。
若题中求半径长或弦的有关问题,常连半径构造等腰三角形或全等三角形。
若题中求弦长、圆心到弦的距离,半径长,通常常连半径或作垂直于弦的线段构造直角三角形。
若题中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化到直角三角形中。
技巧1 连半径构造等腰三角形
典例剖析1
例1.如图,AB是的直径,弦CD与AB交于点E,且E是CD的中点.
(1)求证:;
(2)若,,求的半径.
针对训练1
1.如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
2.如图,AB为的直径,CD是的弦,AB、CD的延长线交于点E,已知,,求的度数.
.
3.如图,内接于,AF是的弦,,垂足为D,点E为弧BF上一点,且.
(1)求证:AE是的直径.
(2)若,,求AC的长.
技巧2连半径构造直角三角形
典例剖析2
例2.如图,内接于,,交交 O于点A,连接,则的度数为( )
A. B. C. D.
针对训练2
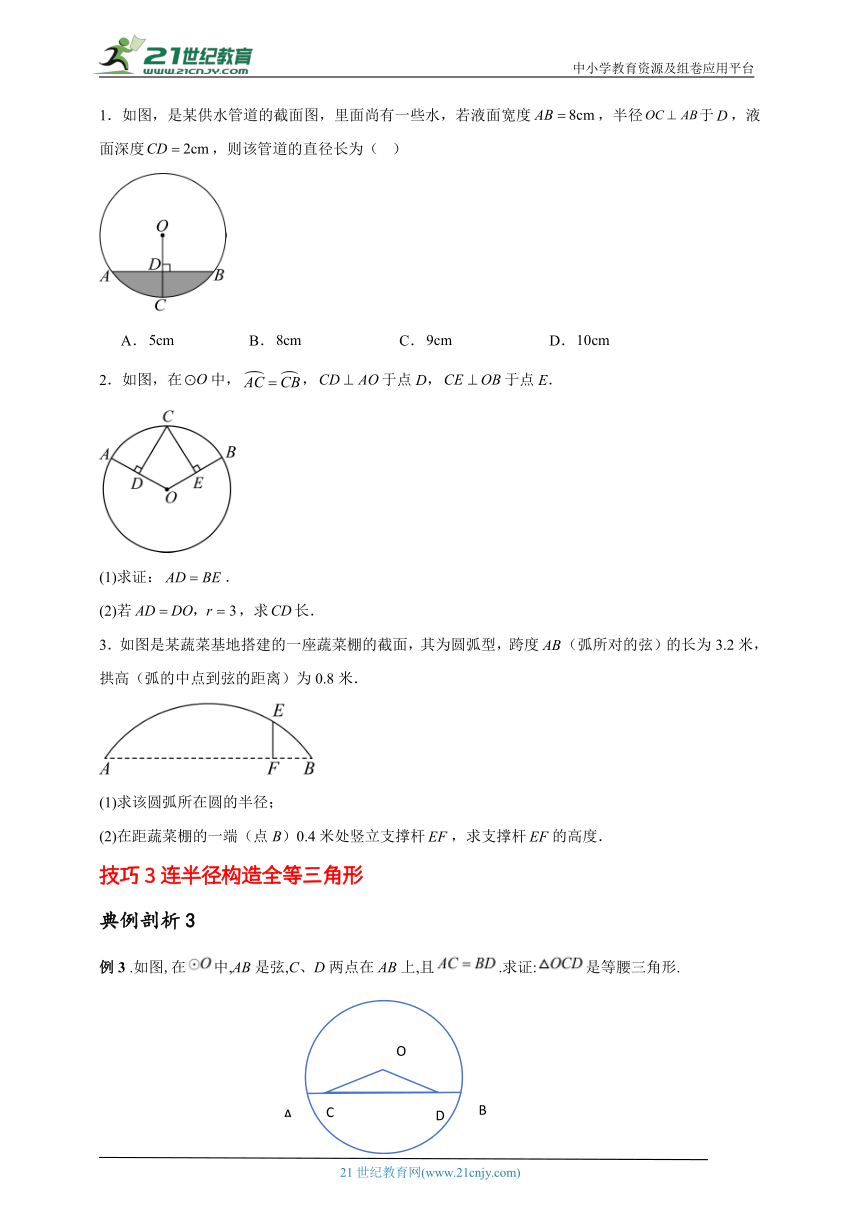
1.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于,液面深度,则该管道的直径长为( )
A. B. C. D.
2.如图,在中,,于点D,于点E.
(1)求证:.
(2)若,求长.
3.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度(弧所对的弦)的长为3.2米,拱高(弧的中点到弦的距离)为0.8米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)0.4米处竖立支撑杆,求支撑杆的高度.
技巧3连半径构造全等三角形
典例剖析3
例3 .如图,在中,AB是弦,C、D两点在AB上,且.求证:是等腰三角形.
针对训练3
1.如图,,D,E分别是半径OA,OB的中点.求证:.
2.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
3.如图,AB,CD为的两条直径,点E,F在直径CD上,且.求证:.
技巧4作垂直于弦的直径构造直角三角形
典例剖析4
例4.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
针对训练4
1.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(见图1,一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦长为8米,半径长为6米,若点C为运行轨道的最低点,则点C到弦所在直线的距离是多少?
2.赵州桥始建于隋代,是世界上现存年代久远、跨度最大、保存最完整的单孔石拱桥(如图1).现有一座仿赵州桥建造的圆拱桥(如图2),已知此圆拱桥的跨径(桥拱圆弧所对的弦的长)为,拱高(桥拱圆弧的中点到弦的距离)为.求此桥拱圆弧的半径(精确到.)
技巧5作直径所对的圆周角构造直角三角形
典例剖析5
例5.如图,是的直径,点C,D,E在上,若,则的度数为( )
A. B. C. D.
针对训练5
1.如图,是的直径,,则的度数为( )
A. B. C. D.
2.如图所示,是的直径,弦交于点E,连接,,若,则的度数是( )
A. B. C. D.
3.如图,AB为的直径,,则的度数为( )
A.80° B.75° C.70° D.65°
4.如图,AB是的直径,点C,D,E在⊙O上,若,则的度数为______.
技巧6作直角所对弦(直径)构造直角三角形
典例剖析6
例6.如图,正方形ABCD内接于,在劣弧AB上取一点E,连接DE,BE,过点D作交于点F,连接BF,AF,且AF与DE相交于点G.
求证:(1)四边形EBFD是矩形;
(2).
针对训练6
1.正方形内接于,如图所示,在劣弧上取一点,连接、,过点作交于点,连接、,且与相交于点,求证:
(1).四边形是矩形;
(2) .
2.如图,在Rt ABC中,AB⊥BC,AB=6,BC=4,P是 ABC内部的一个动点,连接PC,且满足,过点P作PD⊥BC于点D,则∠APB= ;当线段CP最短时, BCP的面积为
技巧7构造圆内接四边形
典例剖析7
例7 .阅读材料,解答问题:
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图1,AB是⊙O的弦,点C在⊙O上,CD⊥AB于点D,在弦AB上取点E,使DE=AD,点F是上的一点,且,连接BF,则BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC,
CD⊥AB于点D,DE=AD,
.
.
,
CF=(依据1),.
四边形ABFC内接于⊙O,
.(依据2)
(1)上述证明过程中的依据1为 ,依据2为 ;
(2)将上述证明过程补充完整.
针对训练7
1.如图,AB是半圆O的直径,C、D、E三点依次在半圆O上,若,,则α与β之间的关系是( )
A. B. C. D.
2.在中,,点A在以BC为直径的半圆外.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图①中作弦EF,使;
(2)在图②中以BC为边作一个的圆周角.
九年级数学上点拨与精练
第24章 圆
24.1 专题 构造圆的基本性质的基本图形的常用辅助线
老师告诉你
用圆的有关性质解题的常用方法是将圆的有关问题转化为三角形问题求解,解题时需要根据图形的特征,作出相对应的辅助线,在图形中构造等腰三角形、直角三角形、全等三角形。
若题中求半径长或弦的有关问题,常连半径构造等腰三角形或全等三角形。
若题中求弦长、圆心到弦的距离,半径长,通常常连半径或作垂直于弦的线段构造直角三角形。
若题中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化到直角三角形中。
技巧1 连半径构造等腰三角形
典例剖析1
例1.如图,AB是的直径,弦CD与AB交于点E,且E是CD的中点.
(1)求证:;
(2)若,,求的半径.
答案:(1)证明见解析
(2)3
解析:(1)证明:连接OC,
∵,E是CD的中点,
∴,
∴,
∴,
∵,
∴,
∴;
(2)设半径为r,
∴,
∵,
∴,
∵,E点是CD的中点,
∴.
由(1)知,,
∴,
∴在中,,
即:,
解得:,
∴半径为3.
.
针对训练1
1.如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
答案:
解析:连接,
,,
,
.
是的外角,
.
,
,
,
.
2.如图,AB为的直径,CD是的弦,AB、CD的延长线交于点E,已知,,求的度数.
答案:54°
解析:连接OD,
,
,又,
,
,
同理
.
3.如图,内接于,AF是的弦,,垂足为D,点E为弧BF上一点,且.
(1)求证:AE是的直径.
(2)若,,求AC的长.
答案:(1)证明:,,
,,
,,
,,
,AE是的直径.
(2)解:连接OC,则,
,
,
,,
是等腰直角三角形,
,,.
技巧2连半径构造直角三角形
典例剖析2
例2.如图,内接于,,交交 O于点A,连接,则的度数为( )
A. B. C. D.
【答案】C
【分析】本题考查了圆周角定理,垂径定理,等边对等角,三角形的内角和定理,连接,,根据圆周角定理得到,根据垂径定理得,根据等腰三角形的性质得出.
【详解】解:如图所示,连接,,
∵,
∴,
∵,,
∴,
∵,
∴,
故选:C.
针对训练2
1.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于,液面深度,则该管道的直径长为( )
A. B. C. D.
【答案】D
【分析】本题主要考查了垂径定理,勾股定理,解一元一次方程等知识点,熟练掌握垂径定理是解题的关键.
连接,由,利用垂径定理可得为的中点,于是可求出的长,设圆的半径为,由可表示出,在中,利用勾股定理即可求出的值,进而可得出答案.
【详解】解:如图,连接,
,
为的中点,
,
设圆的半径为,
在中,
,
根据勾股定理,得:
,
即:,
整理,得:,
解得:,
该管道的直径长为,
故选:.
2.如图,在中,,于点D,于点E.
(1)求证:.
(2)若,求长.
【答案】(1)见解析
(2)
【分析】(1)连接,根据圆心角、弧、弦的关系定理得到,根据角平分线的性质定理证明结论;
(2)求出,根据勾股定理即可求出.
本题考查的是圆心角、弧、弦的关系定理、勾股定理,全等三角形的判定与性质,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
【详解】(1)证明:连接,
,
,
又∵,,
;
∵,
,
∴,
∵,
∴;
(2)解:,,
,
,
.
3.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度(弧所对的弦)的长为3.2米,拱高(弧的中点到弦的距离)为0.8米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)0.4米处竖立支撑杆,求支撑杆的高度.
【答案】(1)2米;
(2)0.4米
【分析】此题主要考查了垂径定理的应用和勾股定理等知识,熟练掌握垂径定理和勾股定理,正确作出辅助线是解题关键.
(1)设弧所在的圆心为,为弧的中点,于,延长至点,设的半径为米,利用勾股定理求出即可;
(2)利用垂径定理以及勾股定理得出的长,再求出的长即可.
【详解】(1)设弧所在的圆心为,为弧的中点,于点,延长经过点,
则(米,
设的半径为米,在中,由勾股定理得:,
即,
解得:,
即该圆弧所在圆的半径为2米;
(2)过作于点,
则(米,米,
在中,(米,
(米,
(米,
即支撑杆的高度为0.4米.
技巧3连半径构造全等三角形
典例剖析3
例3 .如图,在中,AB是弦,C、D两点在AB上,且.求证:是等腰三角形.
答案:证明:连接OA,OB,,.
又,.
,即是等腰三角形.
针对训练3
1.如图,,D,E分别是半径OA,OB的中点.求证:.
答案:证明见解析
解析:证明:连接.
,.
,E分别是OA,OB的中点,
,.
,.
又,.
.
2.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
3.如图,AB,CD为的两条直径,点E,F在直径CD上,且.求证:.
答案:证明:AB,CD为的两条直径,
.
又.
在和中,
,
.
技巧4作垂直于弦的直径构造直角三角形
典例剖析4
例4.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
【答案】2或14
【分析】作于E,延长交于F,连接、,如图,利用平行线的性质,根据垂径定理得到,,则利用勾股定理可计算出,,讨论:当点O在与之间时,;当点O不在与之间时,.
【详解】解:作于E,延长交于F,连接、,如图
∵,,
∴,
∴,
,
在中,,
在中,,
当点O在与之间时,如图1,,
当点O不在与之间时,如图2,,
故答案为:2或14.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.注意分类讨论.
针对训练4
1.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(见图1,一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦长为8米,半径长为6米,若点C为运行轨道的最低点,则点C到弦所在直线的距离是多少?
【答案】米
【分析】本题考查了垂径定理的应用和勾股定理的应用,熟练掌握垂径定理和勾股定理是解题的关键.
连接,交于点D,再由勾股定理得,然后计算即可求解.
【详解】解:连接,交于点D,如图,
即,
∵点C为运行轨道的最低点,,
∴,,
由勾股定理,得,
即,
∴,
故点C到弦所在直线的距离是米.
2.赵州桥始建于隋代,是世界上现存年代久远、跨度最大、保存最完整的单孔石拱桥(如图1).现有一座仿赵州桥建造的圆拱桥(如图2),已知此圆拱桥的跨径(桥拱圆弧所对的弦的长)为,拱高(桥拱圆弧的中点到弦的距离)为.求此桥拱圆弧的半径(精确到.)
【答案】此桥拱圆弧的半径约为
【分析】本题考查了垂径定理的应用以及勾股定理的应用,熟练掌握垂径定理和勾股定理是解题的关键.设弦所在圆的圆心为,弧的中点为,弦的中点为,连接,,,圆的半径为,由垂径定理得,然后在中,由勾股定理得出方程,解方程即可.
【详解】解:如图2所示,设弦所在圆的圆心为,弧的中点为,弦的中点为,连接,,,圆的半径为,
由垂径定理可知,,
,,三点共线,
,,
,
在中,由勾股定理得:,
,
解得,
此桥拱圆弧的半径约为.
技巧5作直径所对的圆周角构造直角三角形
典例剖析5
例5.如图,是的直径,点C,D,E在上,若,则的度数为( )
A. B. C. D.
答案:B
解析:连接,如图,
∵是的直径,
∴,
∵,
∴.
故选:B.
针对训练5
1.如图,是的直径,,则的度数为( )
A. B. C. D.
答案:D
解析:如图:连接,
是的直径,
,
,
,
.
故选:D.
2.如图所示,是的直径,弦交于点E,连接,,若,则的度数是( )
A. B. C. D.
答案:D
解析:如图所示,连接,
∵,
∴,
∵是的直径,
∴,
∴,
故选D.
3.如图,AB为的直径,,则的度数为( )
A.80° B.75° C.70° D.65°
答案:C
解析:连接BC.
∵AB是直径,
∴,
∵,
∴,
故选:C.
4.如图,AB是的直径,点C,D,E在⊙O上,若,则的度数为______.
答案:130°
解析:连接BE,
是直径,
,
,
故答案为:130°.
技巧6作直角所对弦(直径)构造直角三角形
典例剖析6
例6.如图,正方形ABCD内接于,在劣弧AB上取一点E,连接DE,BE,过点D作交于点F,连接BF,AF,且AF与DE相交于点G.
求证:(1)四边形EBFD是矩形;
(2).
答案:(1)如答图,连接BD.
四边形ABCD是正方形,,
BD是的直径,
.
,
,
四边形EBFD是矩形.
(2)如答图,连接OA.
四边形ABCD是正方形,
.
四边形EBFD是矩形,,
,
.
针对训练6
1.正方形内接于,如图所示,在劣弧上取一点,连接、,过点作交于点,连接、,且与相交于点,求证:
(1).四边形是矩形;
(2) .
答案:(1).∵正方形内接于,
∴,
,
又∵,
∴,
∴,
∴四边形是矩形;
(2).∵正方形内接于,
∴弧的度数是,
∴,
又∵,
∴,
∴,
又∵在矩形中, ,
∴.
2.2.如图,在Rt ABC中,AB⊥BC,AB=6,BC=4,P是 ABC内部的一个动点,连接PC,且满足,过点P作PD⊥BC于点D,则∠APB= ;当线段CP最短时, BCP的面积为
【答案】
【分析】(1)由,得到,即可得到;
(2)首先证明点在以为直径的上,连接与交于点,此时最小,利用勾股定理求出即可得到,进而即可求解.
【详解】解:(1)在中,,则,
,
,
,
;
故答案为:;
(2)设的中点为,连接,
则,
点在以为直径的上,连接交于点,此时最小,
在中,,,,
,
,
,
,
,
故答案为:.
【点睛】本题考查点与圆位置关系、圆周角定理、最短问题等知识,解题的关键是确定点P位置,求圆外一点到圆的最小、最大距离.
技巧7构造圆内接四边形
典例剖析7
例7 .阅读材料,解答问题:
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图1,AB是⊙O的弦,点C在⊙O上,CD⊥AB于点D,在弦AB上取点E,使DE=AD,点F是上的一点,且,连接BF,则BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC,
CD⊥AB于点D,DE=AD,
.
.
,
CF=(依据1),.
四边形ABFC内接于⊙O,
.(依据2)
(1)上述证明过程中的依据1为 ,依据2为 ;
(2)将上述证明过程补充完整.
【答案】(1)在同圆中相等的弧所对的弦相等,圆内接四边形的对角互补
(2)见解析
【分析】(1)利用等腰三角形的判定和圆内接四边形的性质解答即可;
(2)在原题的基础上利用全等三角形的判定与性质解答即可得出结论.
【详解】(1)解:上述证明过程中的依据1为:在同圆中相等的弧所对的弦相等,依据2为:圆内接四边形的对角互补.
故答案为:在同圆中相等的弧所对的弦相等,圆内接四边形的对角互补;
(2)解:证明:如图2,连接,,,,
于点,,
.
.
,
,
.
四边形内接于,
,
,
,
在和中,
,
(AAS),
.
【点睛】本题考查了圆内接四边形的性质、圆心角、弦、弧之间的关系定理、三角形全等的判定和性质以及线段垂直平分线的判定和性质,等腰三角形的性质,解题的关键是熟练掌握相关的判定和性质.
针对训练7
1.如图,是半圆O的直径,C、D、E三点依次在半圆O上,若,,则与之间的关系是( )
A. B. C. D.
【答案】A
【分析】连接、、,根据圆内接四边形的性质定理,得到,再根据同弧所对的圆周角相等,得到,由直径所对的圆周角是直角可知,最后根据即可得到与之间的关系.
【详解】解:连接、、,
四边形为圆内接四边形,
,
,
,
,
,
为直径,
,
,
,
,
故选A.
【点睛】本题考查了圆内接四边形的性质定理,同弧所对的圆周角相等,直径所对的圆周角是直角,熟练掌握圆的相关性质是解题关键.
2.在中,,点A在以BC为直径的半圆外.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图①中作弦EF,使;
(2)在图②中以BC为边作一个的圆周角.
答案:(1)见解析;
(2)见解析;
解析:(1)如图:连接DE,DE即为EF,
在中,,
,
又四边形BCEF是圆内接四边形,
,
,
;
(2)如图:过点A作BC的垂线AO,交半圆于P点,连接BP,,
,
又,
.
O
D
C
A
B
O
D
C
A
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上点拨与精练
第24章 圆
24.1 专题 构造圆的基本性质的基本图形的常用辅助线
老师告诉你
用圆的有关性质解题的常用方法是将圆的有关问题转化为三角形问题求解,解题时需要根据图形的特征,作出相对应的辅助线,在图形中构造等腰三角形、直角三角形、全等三角形。
若题中求半径长或弦的有关问题,常连半径构造等腰三角形或全等三角形。
若题中求弦长、圆心到弦的距离,半径长,通常常连半径或作垂直于弦的线段构造直角三角形。
若题中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化到直角三角形中。
技巧1 连半径构造等腰三角形
典例剖析1
例1.如图,AB是的直径,弦CD与AB交于点E,且E是CD的中点.
(1)求证:;
(2)若,,求的半径.
针对训练1
1.如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
2.如图,AB为的直径,CD是的弦,AB、CD的延长线交于点E,已知,,求的度数.
.
3.如图,内接于,AF是的弦,,垂足为D,点E为弧BF上一点,且.
(1)求证:AE是的直径.
(2)若,,求AC的长.
技巧2连半径构造直角三角形
典例剖析2
例2.如图,内接于,,交交 O于点A,连接,则的度数为( )
A. B. C. D.
针对训练2
1.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于,液面深度,则该管道的直径长为( )
A. B. C. D.
2.如图,在中,,于点D,于点E.
(1)求证:.
(2)若,求长.
3.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度(弧所对的弦)的长为3.2米,拱高(弧的中点到弦的距离)为0.8米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)0.4米处竖立支撑杆,求支撑杆的高度.
技巧3连半径构造全等三角形
典例剖析3
例3 .如图,在中,AB是弦,C、D两点在AB上,且.求证:是等腰三角形.
针对训练3
1.如图,,D,E分别是半径OA,OB的中点.求证:.
2.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
3.如图,AB,CD为的两条直径,点E,F在直径CD上,且.求证:.
技巧4作垂直于弦的直径构造直角三角形
典例剖析4
例4.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
针对训练4
1.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(见图1,一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦长为8米,半径长为6米,若点C为运行轨道的最低点,则点C到弦所在直线的距离是多少?
2.赵州桥始建于隋代,是世界上现存年代久远、跨度最大、保存最完整的单孔石拱桥(如图1).现有一座仿赵州桥建造的圆拱桥(如图2),已知此圆拱桥的跨径(桥拱圆弧所对的弦的长)为,拱高(桥拱圆弧的中点到弦的距离)为.求此桥拱圆弧的半径(精确到.)
技巧5作直径所对的圆周角构造直角三角形
典例剖析5
例5.如图,是的直径,点C,D,E在上,若,则的度数为( )
A. B. C. D.
针对训练5
1.如图,是的直径,,则的度数为( )
A. B. C. D.
2.如图所示,是的直径,弦交于点E,连接,,若,则的度数是( )
A. B. C. D.
3.如图,AB为的直径,,则的度数为( )
A.80° B.75° C.70° D.65°
4.如图,AB是的直径,点C,D,E在⊙O上,若,则的度数为______.
技巧6作直角所对弦(直径)构造直角三角形
典例剖析6
例6.如图,正方形ABCD内接于,在劣弧AB上取一点E,连接DE,BE,过点D作交于点F,连接BF,AF,且AF与DE相交于点G.
求证:(1)四边形EBFD是矩形;
(2).
针对训练6
1.正方形内接于,如图所示,在劣弧上取一点,连接、,过点作交于点,连接、,且与相交于点,求证:
(1).四边形是矩形;
(2) .
2.如图,在Rt ABC中,AB⊥BC,AB=6,BC=4,P是 ABC内部的一个动点,连接PC,且满足,过点P作PD⊥BC于点D,则∠APB= ;当线段CP最短时, BCP的面积为
技巧7构造圆内接四边形
典例剖析7
例7 .阅读材料,解答问题:
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图1,AB是⊙O的弦,点C在⊙O上,CD⊥AB于点D,在弦AB上取点E,使DE=AD,点F是上的一点,且,连接BF,则BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC,
CD⊥AB于点D,DE=AD,
.
.
,
CF=(依据1),.
四边形ABFC内接于⊙O,
.(依据2)
(1)上述证明过程中的依据1为 ,依据2为 ;
(2)将上述证明过程补充完整.
针对训练7
1.如图,AB是半圆O的直径,C、D、E三点依次在半圆O上,若,,则α与β之间的关系是( )
A. B. C. D.
2.在中,,点A在以BC为直径的半圆外.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图①中作弦EF,使;
(2)在图②中以BC为边作一个的圆周角.
九年级数学上点拨与精练
第24章 圆
24.1 专题 构造圆的基本性质的基本图形的常用辅助线
老师告诉你
用圆的有关性质解题的常用方法是将圆的有关问题转化为三角形问题求解,解题时需要根据图形的特征,作出相对应的辅助线,在图形中构造等腰三角形、直角三角形、全等三角形。
若题中求半径长或弦的有关问题,常连半径构造等腰三角形或全等三角形。
若题中求弦长、圆心到弦的距离,半径长,通常常连半径或作垂直于弦的线段构造直角三角形。
若题中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化到直角三角形中。
技巧1 连半径构造等腰三角形
典例剖析1
例1.如图,AB是的直径,弦CD与AB交于点E,且E是CD的中点.
(1)求证:;
(2)若,,求的半径.
答案:(1)证明见解析
(2)3
解析:(1)证明:连接OC,
∵,E是CD的中点,
∴,
∴,
∴,
∵,
∴,
∴;
(2)设半径为r,
∴,
∵,
∴,
∵,E点是CD的中点,
∴.
由(1)知,,
∴,
∴在中,,
即:,
解得:,
∴半径为3.
.
针对训练1
1.如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
答案:
解析:连接,
,,
,
.
是的外角,
.
,
,
,
.
2.如图,AB为的直径,CD是的弦,AB、CD的延长线交于点E,已知,,求的度数.
答案:54°
解析:连接OD,
,
,又,
,
,
同理
.
3.如图,内接于,AF是的弦,,垂足为D,点E为弧BF上一点,且.
(1)求证:AE是的直径.
(2)若,,求AC的长.
答案:(1)证明:,,
,,
,,
,,
,AE是的直径.
(2)解:连接OC,则,
,
,
,,
是等腰直角三角形,
,,.
技巧2连半径构造直角三角形
典例剖析2
例2.如图,内接于,,交交 O于点A,连接,则的度数为( )
A. B. C. D.
【答案】C
【分析】本题考查了圆周角定理,垂径定理,等边对等角,三角形的内角和定理,连接,,根据圆周角定理得到,根据垂径定理得,根据等腰三角形的性质得出.
【详解】解:如图所示,连接,,
∵,
∴,
∵,,
∴,
∵,
∴,
故选:C.
针对训练2
1.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于,液面深度,则该管道的直径长为( )
A. B. C. D.
【答案】D
【分析】本题主要考查了垂径定理,勾股定理,解一元一次方程等知识点,熟练掌握垂径定理是解题的关键.
连接,由,利用垂径定理可得为的中点,于是可求出的长,设圆的半径为,由可表示出,在中,利用勾股定理即可求出的值,进而可得出答案.
【详解】解:如图,连接,
,
为的中点,
,
设圆的半径为,
在中,
,
根据勾股定理,得:
,
即:,
整理,得:,
解得:,
该管道的直径长为,
故选:.
2.如图,在中,,于点D,于点E.
(1)求证:.
(2)若,求长.
【答案】(1)见解析
(2)
【分析】(1)连接,根据圆心角、弧、弦的关系定理得到,根据角平分线的性质定理证明结论;
(2)求出,根据勾股定理即可求出.
本题考查的是圆心角、弧、弦的关系定理、勾股定理,全等三角形的判定与性质,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
【详解】(1)证明:连接,
,
,
又∵,,
;
∵,
,
∴,
∵,
∴;
(2)解:,,
,
,
.
3.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度(弧所对的弦)的长为3.2米,拱高(弧的中点到弦的距离)为0.8米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)0.4米处竖立支撑杆,求支撑杆的高度.
【答案】(1)2米;
(2)0.4米
【分析】此题主要考查了垂径定理的应用和勾股定理等知识,熟练掌握垂径定理和勾股定理,正确作出辅助线是解题关键.
(1)设弧所在的圆心为,为弧的中点,于,延长至点,设的半径为米,利用勾股定理求出即可;
(2)利用垂径定理以及勾股定理得出的长,再求出的长即可.
【详解】(1)设弧所在的圆心为,为弧的中点,于点,延长经过点,
则(米,
设的半径为米,在中,由勾股定理得:,
即,
解得:,
即该圆弧所在圆的半径为2米;
(2)过作于点,
则(米,米,
在中,(米,
(米,
(米,
即支撑杆的高度为0.4米.
技巧3连半径构造全等三角形
典例剖析3
例3 .如图,在中,AB是弦,C、D两点在AB上,且.求证:是等腰三角形.
答案:证明:连接OA,OB,,.
又,.
,即是等腰三角形.
针对训练3
1.如图,,D,E分别是半径OA,OB的中点.求证:.
答案:证明见解析
解析:证明:连接.
,.
,E分别是OA,OB的中点,
,.
,.
又,.
.
2.如图,在中,点C是优弧ACB的中点,D,E分别是OA,OB上的点,且,弦CM,CN分别过点D,E.
(1)求证:.
(2)求证:.
答案:(1)如图,连接OC.
点C是优弧ACB的中点,,
.
,,.
,,
.
(2)如图,连接OM,ON.
,
,.
,
,,
.
,,
,.
3.如图,AB,CD为的两条直径,点E,F在直径CD上,且.求证:.
答案:证明:AB,CD为的两条直径,
.
又.
在和中,
,
.
技巧4作垂直于弦的直径构造直角三角形
典例剖析4
例4.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
【答案】2或14
【分析】作于E,延长交于F,连接、,如图,利用平行线的性质,根据垂径定理得到,,则利用勾股定理可计算出,,讨论:当点O在与之间时,;当点O不在与之间时,.
【详解】解:作于E,延长交于F,连接、,如图
∵,,
∴,
∴,
,
在中,,
在中,,
当点O在与之间时,如图1,,
当点O不在与之间时,如图2,,
故答案为:2或14.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.注意分类讨论.
针对训练4
1.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(见图1,一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦长为8米,半径长为6米,若点C为运行轨道的最低点,则点C到弦所在直线的距离是多少?
【答案】米
【分析】本题考查了垂径定理的应用和勾股定理的应用,熟练掌握垂径定理和勾股定理是解题的关键.
连接,交于点D,再由勾股定理得,然后计算即可求解.
【详解】解:连接,交于点D,如图,
即,
∵点C为运行轨道的最低点,,
∴,,
由勾股定理,得,
即,
∴,
故点C到弦所在直线的距离是米.
2.赵州桥始建于隋代,是世界上现存年代久远、跨度最大、保存最完整的单孔石拱桥(如图1).现有一座仿赵州桥建造的圆拱桥(如图2),已知此圆拱桥的跨径(桥拱圆弧所对的弦的长)为,拱高(桥拱圆弧的中点到弦的距离)为.求此桥拱圆弧的半径(精确到.)
【答案】此桥拱圆弧的半径约为
【分析】本题考查了垂径定理的应用以及勾股定理的应用,熟练掌握垂径定理和勾股定理是解题的关键.设弦所在圆的圆心为,弧的中点为,弦的中点为,连接,,,圆的半径为,由垂径定理得,然后在中,由勾股定理得出方程,解方程即可.
【详解】解:如图2所示,设弦所在圆的圆心为,弧的中点为,弦的中点为,连接,,,圆的半径为,
由垂径定理可知,,
,,三点共线,
,,
,
在中,由勾股定理得:,
,
解得,
此桥拱圆弧的半径约为.
技巧5作直径所对的圆周角构造直角三角形
典例剖析5
例5.如图,是的直径,点C,D,E在上,若,则的度数为( )
A. B. C. D.
答案:B
解析:连接,如图,
∵是的直径,
∴,
∵,
∴.
故选:B.
针对训练5
1.如图,是的直径,,则的度数为( )
A. B. C. D.
答案:D
解析:如图:连接,
是的直径,
,
,
,
.
故选:D.
2.如图所示,是的直径,弦交于点E,连接,,若,则的度数是( )
A. B. C. D.
答案:D
解析:如图所示,连接,
∵,
∴,
∵是的直径,
∴,
∴,
故选D.
3.如图,AB为的直径,,则的度数为( )
A.80° B.75° C.70° D.65°
答案:C
解析:连接BC.
∵AB是直径,
∴,
∵,
∴,
故选:C.
4.如图,AB是的直径,点C,D,E在⊙O上,若,则的度数为______.
答案:130°
解析:连接BE,
是直径,
,
,
故答案为:130°.
技巧6作直角所对弦(直径)构造直角三角形
典例剖析6
例6.如图,正方形ABCD内接于,在劣弧AB上取一点E,连接DE,BE,过点D作交于点F,连接BF,AF,且AF与DE相交于点G.
求证:(1)四边形EBFD是矩形;
(2).
答案:(1)如答图,连接BD.
四边形ABCD是正方形,,
BD是的直径,
.
,
,
四边形EBFD是矩形.
(2)如答图,连接OA.
四边形ABCD是正方形,
.
四边形EBFD是矩形,,
,
.
针对训练6
1.正方形内接于,如图所示,在劣弧上取一点,连接、,过点作交于点,连接、,且与相交于点,求证:
(1).四边形是矩形;
(2) .
答案:(1).∵正方形内接于,
∴,
,
又∵,
∴,
∴,
∴四边形是矩形;
(2).∵正方形内接于,
∴弧的度数是,
∴,
又∵,
∴,
∴,
又∵在矩形中, ,
∴.
2.2.如图,在Rt ABC中,AB⊥BC,AB=6,BC=4,P是 ABC内部的一个动点,连接PC,且满足,过点P作PD⊥BC于点D,则∠APB= ;当线段CP最短时, BCP的面积为
【答案】
【分析】(1)由,得到,即可得到;
(2)首先证明点在以为直径的上,连接与交于点,此时最小,利用勾股定理求出即可得到,进而即可求解.
【详解】解:(1)在中,,则,
,
,
,
;
故答案为:;
(2)设的中点为,连接,
则,
点在以为直径的上,连接交于点,此时最小,
在中,,,,
,
,
,
,
,
故答案为:.
【点睛】本题考查点与圆位置关系、圆周角定理、最短问题等知识,解题的关键是确定点P位置,求圆外一点到圆的最小、最大距离.
技巧7构造圆内接四边形
典例剖析7
例7 .阅读材料,解答问题:
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图1,AB是⊙O的弦,点C在⊙O上,CD⊥AB于点D,在弦AB上取点E,使DE=AD,点F是上的一点,且,连接BF,则BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC,
CD⊥AB于点D,DE=AD,
.
.
,
CF=(依据1),.
四边形ABFC内接于⊙O,
.(依据2)
(1)上述证明过程中的依据1为 ,依据2为 ;
(2)将上述证明过程补充完整.
【答案】(1)在同圆中相等的弧所对的弦相等,圆内接四边形的对角互补
(2)见解析
【分析】(1)利用等腰三角形的判定和圆内接四边形的性质解答即可;
(2)在原题的基础上利用全等三角形的判定与性质解答即可得出结论.
【详解】(1)解:上述证明过程中的依据1为:在同圆中相等的弧所对的弦相等,依据2为:圆内接四边形的对角互补.
故答案为:在同圆中相等的弧所对的弦相等,圆内接四边形的对角互补;
(2)解:证明:如图2,连接,,,,
于点,,
.
.
,
,
.
四边形内接于,
,
,
,
在和中,
,
(AAS),
.
【点睛】本题考查了圆内接四边形的性质、圆心角、弦、弧之间的关系定理、三角形全等的判定和性质以及线段垂直平分线的判定和性质,等腰三角形的性质,解题的关键是熟练掌握相关的判定和性质.
针对训练7
1.如图,是半圆O的直径,C、D、E三点依次在半圆O上,若,,则与之间的关系是( )
A. B. C. D.
【答案】A
【分析】连接、、,根据圆内接四边形的性质定理,得到,再根据同弧所对的圆周角相等,得到,由直径所对的圆周角是直角可知,最后根据即可得到与之间的关系.
【详解】解:连接、、,
四边形为圆内接四边形,
,
,
,
,
,
为直径,
,
,
,
,
故选A.
【点睛】本题考查了圆内接四边形的性质定理,同弧所对的圆周角相等,直径所对的圆周角是直角,熟练掌握圆的相关性质是解题关键.
2.在中,,点A在以BC为直径的半圆外.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图①中作弦EF,使;
(2)在图②中以BC为边作一个的圆周角.
答案:(1)见解析;
(2)见解析;
解析:(1)如图:连接DE,DE即为EF,
在中,,
,
又四边形BCEF是圆内接四边形,
,
,
;
(2)如图:过点A作BC的垂线AO,交半圆于P点,连接BP,,
,
又,
.
O
D
C
A
B
O
D
C
A
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
