江苏省镇江市丹阳高中2015-2016学年高二(上)期中数学试卷(实验班)(解析版)
文档属性
| 名称 | 江苏省镇江市丹阳高中2015-2016学年高二(上)期中数学试卷(实验班)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-05 00:00:00 | ||
图片预览




文档简介
2015-2016学年江苏省镇江市丹阳高中高二(上)期中数学试卷(实验班)
一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1},B={0,1,2},则A∩B= .
2.若“x2>1”是“x<a”的必要不充分条件,则a的最大值为 .
3.函数f(x)=1﹣2sin2x的最小正周期为 .
4.已知向量与的夹角是120°,且满足,,则||= .
5.直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,则a= .
6.下列说法正确的序号有 .
(1)如果两个平面有三个公共点,则这两个平面重合.
(2)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都垂直.
(3)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都相交.
(4)m,n为异面直线,过空间任意一点P,一定存在与直线m,n都平行的平面.
7.已知函数f(x)=mx2+lnx﹣2x在定义域内是增函数,则实数m范围为 .
8.若圆锥的高是底面半径和母线长的等比中项,则称此圆锥为“完美圆锥”,已知一完美圆锥的侧面积为2π,则这个圆锥的高为 .
9.已知方程cos2x+4sinx﹣a=0有解,则a的取值范围是 .
10.已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=,则C的离心率e= .
11.等比数列{an}的首项为2,公比为3,前n项和为Sn,若log3[an(S4m+1)]=9,则+的最小值是 .
12.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的取值范围是 .
13.已知函数f(x)满足f(x)=f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
14.若实数a≥0,b≥1且,则2a+2b+1的取值范围为 .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在直角坐标系xOy中,以原点O为圆心作一个单位圆,角α和角β的终边与单位圆分别交于A、B两点,且||=.若0<α<,﹣<β<0,sinβ=﹣.
(1)求△AOB的面积;
(2)求sinα的值.
16.已知四棱锥S﹣ABCD的底面ABCD是边长为2的正方形,侧面SAB是等边三角形,侧面SCD是以CD为斜边的直角三角形,E为CD的中点,M为SB的中点.
(1)求证:CM∥平面SAE;
(2)求证:SE⊥平面SAB;
(3)求三棱锥S﹣AED的体积.
17.(文科)已知数列{an}的前n项的和为Sn,点P(n,Sn)(n∈N*)在函数f(x)=﹣x2+7x的图象上.
(Ⅰ)求数列{an}的通项公式及Sn的最大值;
(Ⅱ)令bn=(n∈N*),求数列{nbn}的前n项的和Tn;
(Ⅲ)设cn=,数列{cn}的前n项的和为Rn,求使不等式Rn>对一切n∈N*都成立的最大正整数k的值.
18.为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
(1)考虑到农村耕地面积的减少,为节约水资源,要减少水渠的过水量,在原水渠内填土,使其成为横断面为等腰梯形的新水渠,新水渠底面与地面平行(不改变渠宽).问新水渠底宽为多少时,所填土的土方量最少?
(2)考虑到新建果园的灌溉需求,要增大水渠的过水量,现把旧水渠改挖(不能填土)成横断面为等腰梯形的新水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽.
19.椭圆=1(a>b>0)的离心率为,左焦点F到右准线l的距离为10,圆G:(x﹣1)2+y2=1.
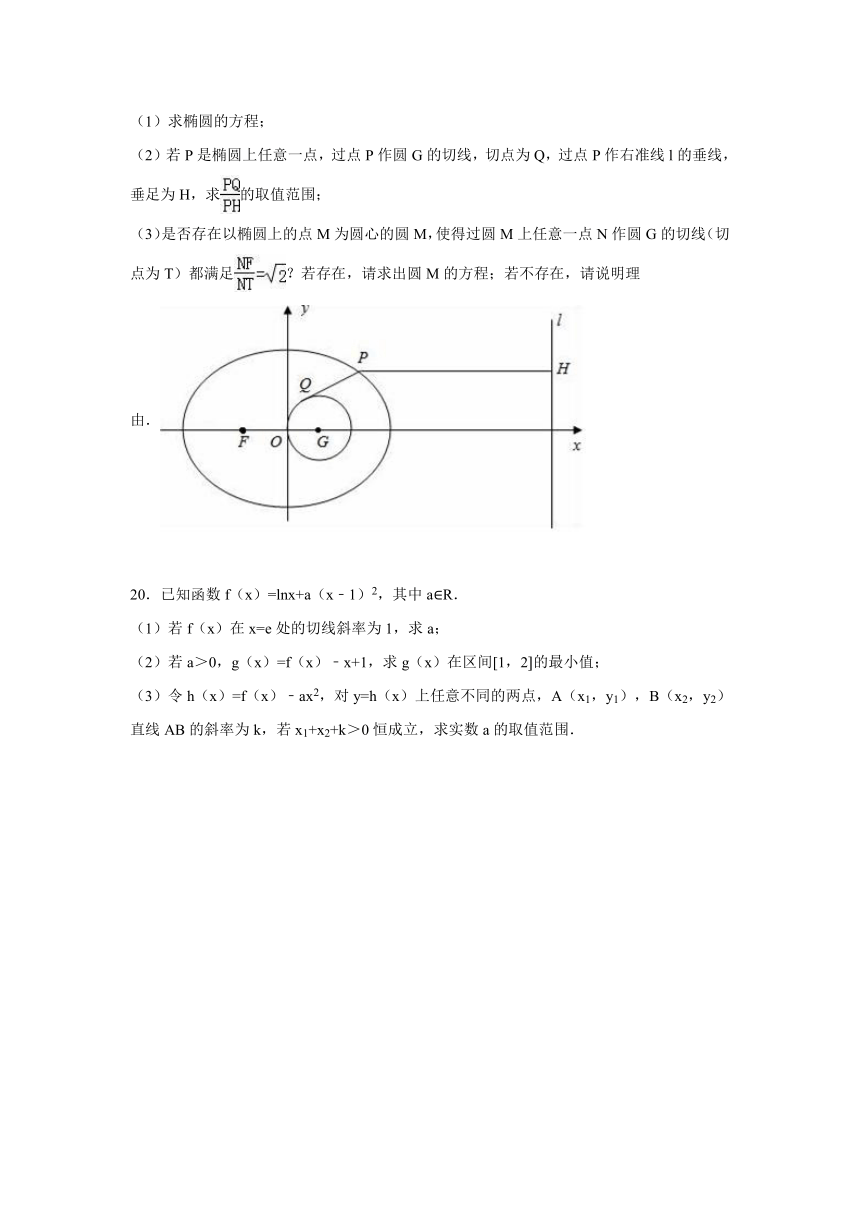
(1)求椭圆的方程;
(2)若P是椭圆上任意一点,过点P作圆G的切线,切点为Q,过点P作右准线l的垂线,垂足为H,求的取值范围;
(3)是否存在以椭圆上的点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)都满足?若存在,请求出圆M的方程;若不存在,请说明理由.
20.已知函数f(x)=lnx+a(x﹣1)2,其中a∈R.
(1)若f(x)在x=e处的切线斜率为1,求a;
(2)若a>0,g(x)=f(x)﹣x+1,求g(x)在区间[1,2]的最小值;
(3)令h(x)=f(x)﹣ax2,对y=h(x)上任意不同的两点,A(x1,y1),B(x2,y2)直线AB的斜率为k,若x1+x2+k>0恒成立,求实数a的取值范围.
2015-2016学年江苏省镇江市丹阳高中高二(上)期中数学试卷(实验班)
参考答案与试题解析
一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1},B={0,1,2},则A∩B= {0,1} .
【考点】交集及其运算.
【专题】集合.
【分析】利用交集的性质求解.
【解答】解:∵集合A={﹣1,0,1},B={0,1,2},
∴A∩B={0,1}.
故答案为:{0,1}.
【点评】本题考查集合的求法,是基础题,解题时要认真审题,注意交集的性质的合理运用.
2.若“x2>1”是“x<a”的必要不充分条件,则a的最大值为 ﹣1 .
【考点】必要条件、充分条件与充要条件的判断.
【专题】计算题.
【分析】因x2>1得x<﹣1或x>1,又“x2>1”是“x<a”的必要不充分条件,知“x<a”可以推出“x2>1”,反之不成立.由此可求出a的最大值.
【解答】解:因x2>1得x<﹣1或x>1,又“x2>1”是“x<a”的必要不充分条件,
知“x<a”可以推出“x2>1”,
反之不成立.
则a的最大值为﹣1.
故答案为﹣1.
【点评】本题考查必要条件、充分条件、充要条件的判断,解题时要认真审题,仔细解答.
3.函数f(x)=1﹣2sin2x的最小正周期为 π .
【考点】三角函数的周期性及其求法;二倍角的余弦.
【专题】计算题.
【分析】先利用二倍角公式对函数解析式进行化简整理,进而利用三角函数最小正周期的公式求得函数的最小正周期.
【解答】解:f(x)=1﹣2sin2x=cos2x
∴函数最小正周期T==π
故答案为:π.
【点评】本题主要考查了二倍角的化简求值和三角函数的周期性及其求法.考查了三角函数的基础的知识的应用.
4.已知向量与的夹角是120°,且满足,,则||= 2 .
【考点】平面向量数量积的坐标表示、模、夹角.
【专题】向量法;平面向量及应用.
【分析】由题意可得向量的模长,由夹角公式可得.
【解答】解:向量与的夹角是120°,且满足,
∴||==,
又∵,
∴||cos120°=﹣,
解得||=2
故答案为:
【点评】本题考查平面向量的数量积和夹角,属基础题.
5.直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,则a= ﹣1 .
【考点】直线的一般式方程与直线的平行关系.
【专题】计算题.
【分析】根据两直线平行,直线方程中一次项系数之比相等,但不等于常数项之比,由此求得a的值.
【解答】解:∵直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,
∴≠,解得 a=﹣1,
故答案为﹣1.
【点评】本题主要考查两直线平行的性质,两直线平行,直线方程中一次项系数之比相等,但不等于常数项之比,属于基础题.
6.下列说法正确的序号有 (2) .
(1)如果两个平面有三个公共点,则这两个平面重合.
(2)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都垂直.
(3)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都相交.
(4)m,n为异面直线,过空间任意一点P,一定存在与直线m,n都平行的平面.
【考点】空间中直线与平面之间的位置关系.
【专题】计算题;转化思想;综合法;空间位置关系与距离.
【分析】在(1)中,如果两个平面有共线的三个公共点,则这两个平面相交;在(2)中,一定能作一条且只能作一条直线l与m,n都垂直;在(3)和(4)举出反例,能得到(3)和(4)都不正确.
【解答】解:(1)如果两个平面有不共线的三个公共点,则这两个平面重合,故(1)错误.
(2)m,n为异面直线,过空间任意一点P,一定能作一条且只能作一条直线l与m,n都垂直,故(2)正确.
(3)过直线m存在一个与直线n平行的平面,
当点P在这个平面内且不在直线m上时,
就不满足结论,故(3)错误;.
(4)过直线m存在一个与直线n平行的平面,
当点P在这个与直线n平行的平面内时,不满足结论,故(4)错误.
故答案为:(2).
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.
7.已知函数f(x)=mx2+lnx﹣2x在定义域内是增函数,则实数m范围为 .
【考点】函数单调性的性质.
【专题】计算题.
【分析】求出f′(x)=2mx+﹣2,因为函数在定义域内是增函数,即要说明f′(x)大于等于0,分离参数求最值,即可得到m的范围.
【解答】解:求导函数,可得f′(x)=2mx+﹣2,x>0,
函数f(x)=mx2+lnx﹣2x在定义域内是增函数,所以f′(x)≥0成立,
所以2mx+﹣2≥0,x>0时恒成立,
所以,
所以﹣2m≤﹣1
所以m≥时,函数f(x)在定义域内是增函数.
故答案为.
【点评】考查学生利用导数研究函数单调性的能力,会找函数单调时自变量的取值范围,属于基础题
8.若圆锥的高是底面半径和母线长的等比中项,则称此圆锥为“完美圆锥”,已知一完美圆锥的侧面积为2π,则这个圆锥的高为 .
【考点】旋转体(圆柱、圆锥、圆台).
【专题】计算题;函数思想;待定系数法;空间位置关系与距离;立体几何.
【分析】设出圆锥的底面半径高、母线,由题意列出关系,求出圆锥的高即可.
【解答】解:设出圆锥的底面半径为r,高为h,母线为L,
由题意可知:h2=Lr,并且×2πr×L=2π,
∴h2=2,
∴h=,
故答案为:
【点评】本题考查旋转体的侧面积,等比中项的知识,是基础题.
9.已知方程cos2x+4sinx﹣a=0有解,则a的取值范围是 [﹣4,4] .
【考点】同角三角函数基本关系的运用.
【专题】三角函数的求值.
【分析】已知方程利用同角三角函数间基本关系化简表示出a,根据方程有解,利用二次函数的性质即可确定出a的范围.
【解答】解:方程cos2x+4sinx﹣a=0,
变形得:1﹣sin2x+4sinx﹣a=0,即a=﹣sin2x+4sinx+1=﹣(sinx﹣2)2+5,
∵﹣1≤sinx≤1,
∴﹣4≤﹣(sinx﹣2)2+5≤4,
则a的取值范围为[﹣4,4].
故答案为:[﹣4,4].
【点评】此题考查了的同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.
10.已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=,则C的离心率e= .
【考点】椭圆的简单性质.
【专题】计算题;压轴题;圆锥曲线的定义、性质与方程.
【分析】设椭圆右焦点为F',连接AF'、BF',可得四边形AFBF'为平行四边形,得|AF|=|BF'|=6.△ABF中利用余弦定理算出|BF|=8,从而得到|AF|2+|BF|2=|AB|2,得∠AFB=90°,所以c=|OF|=|AB|=5.根据椭圆的定义得到2a=|BF|+|BF'|=14,得a=7,最后结合椭圆的离心率公式即可算出椭圆C的离心率.
【解答】解:设椭圆的右焦点为F',连接AF'、BF'
∵AB与FF'互相平分,∴四边形AFBF'为平行四边形,可得|AF|=|BF'|=6
∵△ABF中,|AB|=10,|AF|=6,cos∠ABF=,
∴由余弦定理|AF|2=|AB|2+|BF|2﹣2|AB|×|BF|cos∠ABF,
可得62=102+|BF|2﹣2×10×|BF|×,解之得|BF|=8
由此可得,2a=|BF|+|BF'|=14,得a=7
∵△ABF中,|AF|2+|BF|2=100=|AB|2
∴∠AFB=90°,可得|OF|=|AB|=5,即c=5
因此,椭圆C的离心率e==
故答案为:
【点评】本题给出椭圆经过中心的弦AB与左焦点构成三边分别为6、8、10的直角三角形,求椭圆的离心率.着重考查了椭圆的定义与标准方程、椭圆的简单几何性质等知识,属于中档题.
11.等比数列{an}的首项为2,公比为3,前n项和为Sn,若log3[an(S4m+1)]=9,则+的最小值是 2.5 .
【考点】等比数列的通项公式;基本不等式.
【专题】等差数列与等比数列;不等式的解法及应用.
【分析】根据等比数列{an}的首项为2,公比为3,前n项和为Sn,可得an=2 3n﹣1;Sn=3n﹣1,由log3[an (S4m+1)]=9,可得n+4m=10,进而利用“1”的代换,结合基本不等式,即可得出结论.
【解答】解:∵等比数列{an}的首项为2,公比为3,前n项和为Sn,
∴an=2 3n﹣1;Sn=3n﹣1,
∵log3[an (S4m+1)]=9,
∴(n﹣1)+4m=9,
∴n+4m=10,
∴+=(n+4m)(+)=(17+)≥(17+8)=2.5,
当且仅当m=n=2时取等号,
∴+的最小值是2.5.
故答案为:2.5.
【点评】本题考查等比数列的通项与性质,考查对数运算,考查基本不等式,确定n+4m=3,进而利用“1”的代换,结合基本不等式是关键,属于中档题.
12.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的取值范围是 [4,6] .
【考点】圆的标准方程.
【专题】计算题;直线与圆.
【分析】C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1,设P(a,b)在圆C上,则=(a+m,b),=(a﹣m,b),由已知得m2=a2+b2=|OP|2,m的最值即为|OP|的最值.
【解答】解:圆C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1,
设P(a,b)在圆C上,则=(a+m,b),=(a﹣m,b),
∵∠APB=90°,∴⊥,
∴ =(a+m)(a﹣m)+b2=0,
∴m2=a2+b2=|OP|2,
∴m的最大值即为|OP|的最大值,等于|OC|+r=5+1=6.最小值为5﹣1=4,
∴m的取值范围是[4,6]
故答案为:[4,6].
【点评】本题考查实数的最大值的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.
13.已知函数f(x)满足f(x)=f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 [,) .
【考点】根的存在性及根的个数判断.
【专题】函数的性质及应用;导数的综合应用.
【分析】根据已知即可求得f(x)在[,1]上的解析式为f(x)=﹣lnx,从而可画出f(x)在上的图象,而容易知道g(x)与x轴交点个数便是y=f(x)与y=ax交点个数.通过图象可以看出直线y=ax在其与f(x)=lnx的切点和曲线y=f(x)的右端点之间,从而分别求出相切时a的值和经过右端点时a的值即可.
【解答】解:设x∈,则∈[1,3];
∴根据条件;
g(x)与x轴有三个不同的交点即表示函数y=f(x)和函数y=ax有三个不同交点,如图所示:
由图可看出当直线y=ax与曲线f(x)=lnx,x∈[1,3],相切时直线y=ax和曲线y=f(x)有两个公共点;
若直线y=ax再向下旋转便有三个交点,直到y=ax经过曲线y=f(x)的右端点,再向下旋转便成了两个交点;
设切点为(x0,lnx0),∴,又,∴;
∴此时lnx0=1,x0=e;
∴此时a=;
y=f(x)的右端点坐标为(3,ln3);
∴直线y=ax经过右端点时,a=;
∴实数a的取值范围是.
故答案为:[).
【点评】考查通过将定义域转变到已知函数的定义域上求函数解析式的方法,数形结合解题的方法,以及直线和曲线相切时的斜率和曲线在切点处导数的关系.
14.若实数a≥0,b≥1且,则2a+2b+1的取值范围为 [7,9] .
【考点】有理数指数幂的化简求值.
【专题】计算题;转化思想;综合法;函数的性质及应用.
【分析】由已知得(2a﹣1)2=2b(4﹣2b)≥0,从而得到1≤b≤2,由此能求出2a+2b+1的取值范围.
【解答】解:∵实数a≥0,b≥1且,
∴(2a)2+(2b)2=2×2a+4×2b﹣1,
∴(2a﹣1)2=2b(4﹣2b)≥0,
∴4﹣2b≥0,
解得1≤b≤2,∴4≤2b+1≤8,
∵(2a﹣1)2=2b(4﹣2b)≥0,
∴b=1时,2a=3,2a+2b+1=7,
b=2时,2a=1,2a+2b+1=9,
∴7≤2a+2b+1≤9,
∴2a+2b+1的取值范围为[7,9].
故答案为:[7,9].
【点评】本题考查有理数指数幂代数和的取值范围的求法,是基础题,解题时要认真审题,注意有理数指数幂的运算法则的合理运用.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在直角坐标系xOy中,以原点O为圆心作一个单位圆,角α和角β的终边与单位圆分别交于A、B两点,且||=.若0<α<,﹣<β<0,sinβ=﹣.
(1)求△AOB的面积;
(2)求sinα的值.
【考点】余弦定理;正弦定理.
【专题】计算题;转化思想;数形结合法;解三角形;平面向量及应用.
【分析】(1)根据题意设出,,利用向量法则根据﹣表示出,利用向量模的定义列出关系式,整理后利用两角和与差的余弦函数公式即可求出cos(α﹣β)的值,由α与β的范围求出α﹣β的范围,利用同角三角函数间的基本关系求出sin(α﹣β),由三角形面积公式即可得解.
(2)可先求cosβ的值,所求式子变形后,利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值.
【解答】解:(1)根据题意设=(cosα,sinα),=(cosβ,sinβ),
∴=﹣=(cosβ﹣cosα,sinβ﹣sinα),
∴||2=(cosβ﹣cosα)2+(sinβ﹣sinα)2=,即2﹣2(cosβcosα+sinβsinα)=,
∴cos(α﹣β)=cosβcosα+sinβsinα=;
∵0<α<,﹣<β<0,
∴0<α﹣β<π,
∴sin∠AOB=sin(α﹣β)==,
又∵|OA|=1,|OB|=1,
∴S△AOB=|OA| |OB|sin∠AOB==.
(2)∵sinβ=﹣,
∴cosβ==,
则sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ=×﹣×=.
【点评】此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,考查了平面向量的运算,熟练掌握公式是解本题的关键,属于中档题.
16.已知四棱锥S﹣ABCD的底面ABCD是边长为2的正方形,侧面SAB是等边三角形,侧面SCD是以CD为斜边的直角三角形,E为CD的中点,M为SB的中点.
(1)求证:CM∥平面SAE;
(2)求证:SE⊥平面SAB;
(3)求三棱锥S﹣AED的体积.
【考点】直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定.
【专题】计算题;证明题;空间位置关系与距离.
【分析】(1)取SA的中点N,连接MN.△ASB中利用中位线定理,证出MN∥AB且MN=AB,而正方形ABCD中E为CD中点,可得CE∥AB且CE=AB,从而得到CENM为平行四边形,得CM∥EN.最后用线面平行的判定定理,即可证出CM∥平面SAE;
(2)Rt△SCD中,E为斜边中点,可得SE=CD=1.△ESA中算出SE2+SA2=5=AE2,从而得到ES⊥SA,同理△ESB中证出ES⊥SB,结合SA、SB是平面SAB内的相交直线,可证出SE⊥平面SAB.
(3)根据正方形的性质可得S△AED=S△ABE,从而得到VS﹣AED=VS﹣AEB=VE﹣SAB,由(2)得SE是三棱锥E﹣SAB的高,从而算出VE﹣SAB=,由此即可得到VS﹣AED=VE﹣SAB=.
【解答】解:(1)取SA的中点N,连接MN,EN
∵M为SB的中点,N为SA的中点,∴MN∥AB,且MN=AB,
又E是CD的中点,∴CE∥AB,且CE=AB,
∴MN∥CE,且MN=CE,∴四边形CENM为平行四边形,
∴CM∥EN,又EN 平面SAE,CM 平面SAE,
∴CM∥平面SAE.
(2)∵侧面SCD为直角三角形,∠CSD=90°,E为CD的中点,
∴SE=CD=1,
又∵SA=AB=2,AE=,
∴SE2+SA2=5=AE2,可得ES⊥SA,同理可证ES⊥SB,
∵SA∩SB=S,SA、SB 平面SAB,∴SE⊥平面SAB.
(3)根据题意,得VS﹣AED=VS﹣AEB=VE﹣SAB,
∵SE⊥平面SAB,可得SE是三棱锥E﹣SAB的高
∴VE﹣SAB=S△SAB×SE==
因此,三棱锥S﹣AED的体积为VS﹣AED=VE﹣SAB=×=.
【点评】本题在四棱锥中证明线面平行、线面垂直,并求三棱锥的体积.着重考查了空间直线与平面平行的判定定理、直线与平面垂直的判定定理和锥体体积公式等知识,属于中档题.
17.(文科)已知数列{an}的前n项的和为Sn,点P(n,Sn)(n∈N*)在函数f(x)=﹣x2+7x的图象上.
(Ⅰ)求数列{an}的通项公式及Sn的最大值;
(Ⅱ)令bn=(n∈N*),求数列{nbn}的前n项的和Tn;
(Ⅲ)设cn=,数列{cn}的前n项的和为Rn,求使不等式Rn>对一切n∈N*都成立的最大正整数k的值.
【考点】数列的求和;数列的函数特性.
【专题】等差数列与等比数列.
【分析】(1)由于点P(n,Sn)(n∈N)在函数f(x)=﹣x2+7x的图象上.可得Sn.利用当n≥2时,an=Sn﹣Sn﹣1,当n=1时,a1=S1,即可得出an.再利用二次函数的单调性即可得出Sn的最值;
(2)利用“错位相减法”即可得出;
(3)利用“裂项求和”得出Rn,求出其最小值即可.
【解答】解:(1)∵点P(n,Sn)(n∈N)在函数f(x)=﹣x2+7x的图象上.
∴,
当n≥2时,an=Sn﹣Sn﹣1=﹣2n+8
当n=1时,a1=S1=6满足上式,
∴an=﹣2n+8.
又=,且n∈N*
∴当n=3或4时,Sn取得最大值12.
(2)由题意知
∴数列{nbn}的前n项的和为
∴,
相减得,
∴.
(3)由(1)得=
∴=
易知Rn在n∈N*上单调递增,∴Rn的最小值为
不等式对一切n∈N*都成立,则,即k<19.
所以最大正整数k的值为18.
【点评】本题考查了利用“当n≥2时,an=Sn﹣Sn﹣1,当n=1时,a1=S1”得出an、二次函数的单调性、“错位相减法”、“裂项求和”、恒成立问题等基础知识与基本技能方法,属于难题.
18.为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
(1)考虑到农村耕地面积的减少,为节约水资源,要减少水渠的过水量,在原水渠内填土,使其成为横断面为等腰梯形的新水渠,新水渠底面与地面平行(不改变渠宽).问新水渠底宽为多少时,所填土的土方量最少?
(2)考虑到新建果园的灌溉需求,要增大水渠的过水量,现把旧水渠改挖(不能填土)成横断面为等腰梯形的新水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽.
【考点】函数最值的应用.
【专题】应用题;导数的综合应用.
【分析】(1)建立坐标系,设抛物线的方程为x2=2py(p>0).由已知点P(2,2)在抛物线上,推导出抛物线的方程,可得梯形APQB面积,利用导数可得结论.
(2)为了使挖掉的土最少,等腰梯形的两腰必须与抛物线相切,设切点M(t, t2),t>0.则函数在点M的切线方程为y﹣t2=t(x﹣t),由此能推导出设计改挖后的水渠的底宽为m时,可使用权所挖土的土方量最少.
【解答】解:(1)建立如图的坐标系,
设抛物线的方程为x2=2py(p>0).
由已知点P(2,2)在抛物线上,得p=1,
∴抛物线的方程为x2=2y,
设A(t, t2),则此时梯形APQB面积为S(t)=(2t+4)(2﹣t2),
∴S′(t)=﹣,t=,
t∈(0,),S′(t)>0,t∈(,2),S′(t)<0
∴t=,Smax(t)=,
∴新水渠底宽为m时,所填土的土方量最少;
(2)为了使挖掉的土最少,等腰梯形的两腰必须与抛物线相切,
如图,
设切点M(t, t2),t>0.
则函数在点M的切线方程为y﹣t2=t(x﹣t),
令y=0,y=2,得A(t,0),B(,2),
∴此时梯形OABC的面积为S(t)=(t+) 2=t+≥2,
当且仅当t=时,等号成立,
此时|OA|=,
∴设计改挖后的水渠的底宽为m时,土方量最少.
【点评】本题考查函数在生产生活中的实际应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数知识、基本不等式的合理运用.
19.椭圆=1(a>b>0)的离心率为,左焦点F到右准线l的距离为10,圆G:(x﹣1)2+y2=1.
(1)求椭圆的方程;
(2)若P是椭圆上任意一点,过点P作圆G的切线,切点为Q,过点P作右准线l的垂线,垂足为H,求的取值范围;
(3)是否存在以椭圆上的点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)都满足?若存在,请求出圆M的方程;若不存在,请说明理由.
【考点】椭圆的简单性质.
【专题】压轴题;探究型;转化思想;数形结合法;圆锥曲线的定义、性质与方程.
【分析】(1)由题意可得,解方程组得到a,c的值,结合隐含条件求得b,则椭圆方程可求;
(2)圆G:(x﹣1)2+y2=1的圆心在椭圆的右焦点上,把转化为含椭圆离心率与PH的式子,求出PH的范围可得答案;
(3)设圆M:(x﹣m)2+(y﹣n)2=r2(r>0)满足条件,N(x,y),可知点(m,n)满足,化圆的方程为一般式,由得x2+y2﹣6x﹣1=0,
代入圆的方程可得2(m﹣3)x+2ny﹣m2﹣n2﹣1+r2=0对圆M上点N(x,y)恒成立,由系数为0求得m,n,r的值,验证满足后可得答案.
【解答】解:(1)由题意可得,解得a=3,c=1,∴b2=a2﹣c2=8.
则椭圆方程为;
(2)圆G:(x﹣1)2+y2=1的圆心在椭圆的右焦点上,
∴,
∵e=,PH∈[]=[6,12],
∴ [],则∈[];
(3)设圆M:(x﹣m)2+(y﹣n)2=r2(r>0)满足条件,N(x,y),
其中点(m,n)满足,则x2+y2=2mx+2ny﹣m2﹣n2+r2,
,
要使即NF2=2NT2,即x2+y2﹣6x﹣1=0,
代入x2+y2=2mx+2ny﹣m2﹣n2+r2,
得2(m﹣3)x+2ny﹣m2﹣n2﹣1+r2=0对圆M上点N(x,y)恒成立,
只要使,得,经检验m=3,n=0满足,
故存在以椭圆上点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)
都满足,圆M的方程为(x﹣3)2+y2=10.
【点评】本题考查椭圆的简单性质,考查了圆与圆锥曲线的位置关系,对于(3)的求解是该题的难点所在,与恒成立问题进行了交汇,试题设置难度较大.
20.已知函数f(x)=lnx+a(x﹣1)2,其中a∈R.
(1)若f(x)在x=e处的切线斜率为1,求a;
(2)若a>0,g(x)=f(x)﹣x+1,求g(x)在区间[1,2]的最小值;
(3)令h(x)=f(x)﹣ax2,对y=h(x)上任意不同的两点,A(x1,y1),B(x2,y2)直线AB的斜率为k,若x1+x2+k>0恒成立,求实数a的取值范围.
【考点】利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.
【专题】导数的概念及应用;导数的综合应用;不等式的解法及应用.
【分析】(1)求得导数,求出切线的斜率,解方程可得a:
(2)化简g(x),求得导数,讨论当a≥时,当0<a≤时,当<a<时,由单调区间,即可得到最小值;
(3)运用斜率公式,化简整理,即有m(x)=lnx+x2﹣a(2x﹣1)在(0,+∞)上递增,运用导数判断单调性,结合恒成立思想,计算即可得到a的范围.
【解答】解:(1)函数f(x)=lnx+a(x﹣1)2的导数为f′(x)=+2a(x﹣1),
f(x)在x=e处的切线斜率为1,即有+2a(e﹣1)=1,
解得a=;
(2)g(x)=f(x)﹣x+1=lnx+a(x﹣1)2﹣x+1,
g′(x)=+2a(x﹣1)﹣1=,
当a≥时,在[1,2]上g′(x)>0,g(x)递增,
即有x=1处取得最小值,且为0;
当0<a≤时,在[1,2]上g′(x)<0,g(x)递减,
即有x=2处取得最小值,且为ln2+a﹣1;
当<a<时,g(x)在[1,)递减,在(,2)递增,
即有x=处取得最小值,且为﹣ln(2a)+a(﹣1)2﹣+1;
(3)h(x)=f(x)﹣ax2=lnx﹣a(2x﹣1),
x1+x2+k>0恒成立,
即为x1+x2+>0恒成立,
即有>0,
即为m(x)=lnx+x2﹣a(2x﹣1)在(0,+∞)上递增,
即有m′(x)=+2x﹣2a≥0恒成立,
即为2a≤2x+的最小值,
由2x+≥2=2(当且仅当x=,等号成立),
则2a≤2,
解得a≤.
【点评】本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用单调性的定义和构造函数的方法,属于中档题.
一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1},B={0,1,2},则A∩B= .
2.若“x2>1”是“x<a”的必要不充分条件,则a的最大值为 .
3.函数f(x)=1﹣2sin2x的最小正周期为 .
4.已知向量与的夹角是120°,且满足,,则||= .
5.直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,则a= .
6.下列说法正确的序号有 .
(1)如果两个平面有三个公共点,则这两个平面重合.
(2)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都垂直.
(3)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都相交.
(4)m,n为异面直线,过空间任意一点P,一定存在与直线m,n都平行的平面.
7.已知函数f(x)=mx2+lnx﹣2x在定义域内是增函数,则实数m范围为 .
8.若圆锥的高是底面半径和母线长的等比中项,则称此圆锥为“完美圆锥”,已知一完美圆锥的侧面积为2π,则这个圆锥的高为 .
9.已知方程cos2x+4sinx﹣a=0有解,则a的取值范围是 .
10.已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=,则C的离心率e= .
11.等比数列{an}的首项为2,公比为3,前n项和为Sn,若log3[an(S4m+1)]=9,则+的最小值是 .
12.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的取值范围是 .
13.已知函数f(x)满足f(x)=f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 .
14.若实数a≥0,b≥1且,则2a+2b+1的取值范围为 .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在直角坐标系xOy中,以原点O为圆心作一个单位圆,角α和角β的终边与单位圆分别交于A、B两点,且||=.若0<α<,﹣<β<0,sinβ=﹣.
(1)求△AOB的面积;
(2)求sinα的值.
16.已知四棱锥S﹣ABCD的底面ABCD是边长为2的正方形,侧面SAB是等边三角形,侧面SCD是以CD为斜边的直角三角形,E为CD的中点,M为SB的中点.
(1)求证:CM∥平面SAE;
(2)求证:SE⊥平面SAB;
(3)求三棱锥S﹣AED的体积.
17.(文科)已知数列{an}的前n项的和为Sn,点P(n,Sn)(n∈N*)在函数f(x)=﹣x2+7x的图象上.
(Ⅰ)求数列{an}的通项公式及Sn的最大值;
(Ⅱ)令bn=(n∈N*),求数列{nbn}的前n项的和Tn;
(Ⅲ)设cn=,数列{cn}的前n项的和为Rn,求使不等式Rn>对一切n∈N*都成立的最大正整数k的值.
18.为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
(1)考虑到农村耕地面积的减少,为节约水资源,要减少水渠的过水量,在原水渠内填土,使其成为横断面为等腰梯形的新水渠,新水渠底面与地面平行(不改变渠宽).问新水渠底宽为多少时,所填土的土方量最少?
(2)考虑到新建果园的灌溉需求,要增大水渠的过水量,现把旧水渠改挖(不能填土)成横断面为等腰梯形的新水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽.
19.椭圆=1(a>b>0)的离心率为,左焦点F到右准线l的距离为10,圆G:(x﹣1)2+y2=1.
(1)求椭圆的方程;
(2)若P是椭圆上任意一点,过点P作圆G的切线,切点为Q,过点P作右准线l的垂线,垂足为H,求的取值范围;
(3)是否存在以椭圆上的点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)都满足?若存在,请求出圆M的方程;若不存在,请说明理由.
20.已知函数f(x)=lnx+a(x﹣1)2,其中a∈R.
(1)若f(x)在x=e处的切线斜率为1,求a;
(2)若a>0,g(x)=f(x)﹣x+1,求g(x)在区间[1,2]的最小值;
(3)令h(x)=f(x)﹣ax2,对y=h(x)上任意不同的两点,A(x1,y1),B(x2,y2)直线AB的斜率为k,若x1+x2+k>0恒成立,求实数a的取值范围.
2015-2016学年江苏省镇江市丹阳高中高二(上)期中数学试卷(实验班)
参考答案与试题解析
一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1},B={0,1,2},则A∩B= {0,1} .
【考点】交集及其运算.
【专题】集合.
【分析】利用交集的性质求解.
【解答】解:∵集合A={﹣1,0,1},B={0,1,2},
∴A∩B={0,1}.
故答案为:{0,1}.
【点评】本题考查集合的求法,是基础题,解题时要认真审题,注意交集的性质的合理运用.
2.若“x2>1”是“x<a”的必要不充分条件,则a的最大值为 ﹣1 .
【考点】必要条件、充分条件与充要条件的判断.
【专题】计算题.
【分析】因x2>1得x<﹣1或x>1,又“x2>1”是“x<a”的必要不充分条件,知“x<a”可以推出“x2>1”,反之不成立.由此可求出a的最大值.
【解答】解:因x2>1得x<﹣1或x>1,又“x2>1”是“x<a”的必要不充分条件,
知“x<a”可以推出“x2>1”,
反之不成立.
则a的最大值为﹣1.
故答案为﹣1.
【点评】本题考查必要条件、充分条件、充要条件的判断,解题时要认真审题,仔细解答.
3.函数f(x)=1﹣2sin2x的最小正周期为 π .
【考点】三角函数的周期性及其求法;二倍角的余弦.
【专题】计算题.
【分析】先利用二倍角公式对函数解析式进行化简整理,进而利用三角函数最小正周期的公式求得函数的最小正周期.
【解答】解:f(x)=1﹣2sin2x=cos2x
∴函数最小正周期T==π
故答案为:π.
【点评】本题主要考查了二倍角的化简求值和三角函数的周期性及其求法.考查了三角函数的基础的知识的应用.
4.已知向量与的夹角是120°,且满足,,则||= 2 .
【考点】平面向量数量积的坐标表示、模、夹角.
【专题】向量法;平面向量及应用.
【分析】由题意可得向量的模长,由夹角公式可得.
【解答】解:向量与的夹角是120°,且满足,
∴||==,
又∵,
∴||cos120°=﹣,
解得||=2
故答案为:
【点评】本题考查平面向量的数量积和夹角,属基础题.
5.直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,则a= ﹣1 .
【考点】直线的一般式方程与直线的平行关系.
【专题】计算题.
【分析】根据两直线平行,直线方程中一次项系数之比相等,但不等于常数项之比,由此求得a的值.
【解答】解:∵直线ax+2y+6=0与直线x+(a﹣1)y+(a2﹣1)=0平行,
∴≠,解得 a=﹣1,
故答案为﹣1.
【点评】本题主要考查两直线平行的性质,两直线平行,直线方程中一次项系数之比相等,但不等于常数项之比,属于基础题.
6.下列说法正确的序号有 (2) .
(1)如果两个平面有三个公共点,则这两个平面重合.
(2)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都垂直.
(3)m,n为异面直线,过空间任意一点P,一定能作一条直线l与m,n都相交.
(4)m,n为异面直线,过空间任意一点P,一定存在与直线m,n都平行的平面.
【考点】空间中直线与平面之间的位置关系.
【专题】计算题;转化思想;综合法;空间位置关系与距离.
【分析】在(1)中,如果两个平面有共线的三个公共点,则这两个平面相交;在(2)中,一定能作一条且只能作一条直线l与m,n都垂直;在(3)和(4)举出反例,能得到(3)和(4)都不正确.
【解答】解:(1)如果两个平面有不共线的三个公共点,则这两个平面重合,故(1)错误.
(2)m,n为异面直线,过空间任意一点P,一定能作一条且只能作一条直线l与m,n都垂直,故(2)正确.
(3)过直线m存在一个与直线n平行的平面,
当点P在这个平面内且不在直线m上时,
就不满足结论,故(3)错误;.
(4)过直线m存在一个与直线n平行的平面,
当点P在这个与直线n平行的平面内时,不满足结论,故(4)错误.
故答案为:(2).
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.
7.已知函数f(x)=mx2+lnx﹣2x在定义域内是增函数,则实数m范围为 .
【考点】函数单调性的性质.
【专题】计算题.
【分析】求出f′(x)=2mx+﹣2,因为函数在定义域内是增函数,即要说明f′(x)大于等于0,分离参数求最值,即可得到m的范围.
【解答】解:求导函数,可得f′(x)=2mx+﹣2,x>0,
函数f(x)=mx2+lnx﹣2x在定义域内是增函数,所以f′(x)≥0成立,
所以2mx+﹣2≥0,x>0时恒成立,
所以,
所以﹣2m≤﹣1
所以m≥时,函数f(x)在定义域内是增函数.
故答案为.
【点评】考查学生利用导数研究函数单调性的能力,会找函数单调时自变量的取值范围,属于基础题
8.若圆锥的高是底面半径和母线长的等比中项,则称此圆锥为“完美圆锥”,已知一完美圆锥的侧面积为2π,则这个圆锥的高为 .
【考点】旋转体(圆柱、圆锥、圆台).
【专题】计算题;函数思想;待定系数法;空间位置关系与距离;立体几何.
【分析】设出圆锥的底面半径高、母线,由题意列出关系,求出圆锥的高即可.
【解答】解:设出圆锥的底面半径为r,高为h,母线为L,
由题意可知:h2=Lr,并且×2πr×L=2π,
∴h2=2,
∴h=,
故答案为:
【点评】本题考查旋转体的侧面积,等比中项的知识,是基础题.
9.已知方程cos2x+4sinx﹣a=0有解,则a的取值范围是 [﹣4,4] .
【考点】同角三角函数基本关系的运用.
【专题】三角函数的求值.
【分析】已知方程利用同角三角函数间基本关系化简表示出a,根据方程有解,利用二次函数的性质即可确定出a的范围.
【解答】解:方程cos2x+4sinx﹣a=0,
变形得:1﹣sin2x+4sinx﹣a=0,即a=﹣sin2x+4sinx+1=﹣(sinx﹣2)2+5,
∵﹣1≤sinx≤1,
∴﹣4≤﹣(sinx﹣2)2+5≤4,
则a的取值范围为[﹣4,4].
故答案为:[﹣4,4].
【点评】此题考查了的同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.
10.已知椭圆的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=,则C的离心率e= .
【考点】椭圆的简单性质.
【专题】计算题;压轴题;圆锥曲线的定义、性质与方程.
【分析】设椭圆右焦点为F',连接AF'、BF',可得四边形AFBF'为平行四边形,得|AF|=|BF'|=6.△ABF中利用余弦定理算出|BF|=8,从而得到|AF|2+|BF|2=|AB|2,得∠AFB=90°,所以c=|OF|=|AB|=5.根据椭圆的定义得到2a=|BF|+|BF'|=14,得a=7,最后结合椭圆的离心率公式即可算出椭圆C的离心率.
【解答】解:设椭圆的右焦点为F',连接AF'、BF'
∵AB与FF'互相平分,∴四边形AFBF'为平行四边形,可得|AF|=|BF'|=6
∵△ABF中,|AB|=10,|AF|=6,cos∠ABF=,
∴由余弦定理|AF|2=|AB|2+|BF|2﹣2|AB|×|BF|cos∠ABF,
可得62=102+|BF|2﹣2×10×|BF|×,解之得|BF|=8
由此可得,2a=|BF|+|BF'|=14,得a=7
∵△ABF中,|AF|2+|BF|2=100=|AB|2
∴∠AFB=90°,可得|OF|=|AB|=5,即c=5
因此,椭圆C的离心率e==
故答案为:
【点评】本题给出椭圆经过中心的弦AB与左焦点构成三边分别为6、8、10的直角三角形,求椭圆的离心率.着重考查了椭圆的定义与标准方程、椭圆的简单几何性质等知识,属于中档题.
11.等比数列{an}的首项为2,公比为3,前n项和为Sn,若log3[an(S4m+1)]=9,则+的最小值是 2.5 .
【考点】等比数列的通项公式;基本不等式.
【专题】等差数列与等比数列;不等式的解法及应用.
【分析】根据等比数列{an}的首项为2,公比为3,前n项和为Sn,可得an=2 3n﹣1;Sn=3n﹣1,由log3[an (S4m+1)]=9,可得n+4m=10,进而利用“1”的代换,结合基本不等式,即可得出结论.
【解答】解:∵等比数列{an}的首项为2,公比为3,前n项和为Sn,
∴an=2 3n﹣1;Sn=3n﹣1,
∵log3[an (S4m+1)]=9,
∴(n﹣1)+4m=9,
∴n+4m=10,
∴+=(n+4m)(+)=(17+)≥(17+8)=2.5,
当且仅当m=n=2时取等号,
∴+的最小值是2.5.
故答案为:2.5.
【点评】本题考查等比数列的通项与性质,考查对数运算,考查基本不等式,确定n+4m=3,进而利用“1”的代换,结合基本不等式是关键,属于中档题.
12.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的取值范围是 [4,6] .
【考点】圆的标准方程.
【专题】计算题;直线与圆.
【分析】C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1,设P(a,b)在圆C上,则=(a+m,b),=(a﹣m,b),由已知得m2=a2+b2=|OP|2,m的最值即为|OP|的最值.
【解答】解:圆C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1,
设P(a,b)在圆C上,则=(a+m,b),=(a﹣m,b),
∵∠APB=90°,∴⊥,
∴ =(a+m)(a﹣m)+b2=0,
∴m2=a2+b2=|OP|2,
∴m的最大值即为|OP|的最大值,等于|OC|+r=5+1=6.最小值为5﹣1=4,
∴m的取值范围是[4,6]
故答案为:[4,6].
【点评】本题考查实数的最大值的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.
13.已知函数f(x)满足f(x)=f(),当x∈[1,3]时,f(x)=lnx,若在区间[,3]内,函数g(x)=f(x)﹣ax与x轴有三个不同的交点,则实数a的取值范围是 [,) .
【考点】根的存在性及根的个数判断.
【专题】函数的性质及应用;导数的综合应用.
【分析】根据已知即可求得f(x)在[,1]上的解析式为f(x)=﹣lnx,从而可画出f(x)在上的图象,而容易知道g(x)与x轴交点个数便是y=f(x)与y=ax交点个数.通过图象可以看出直线y=ax在其与f(x)=lnx的切点和曲线y=f(x)的右端点之间,从而分别求出相切时a的值和经过右端点时a的值即可.
【解答】解:设x∈,则∈[1,3];
∴根据条件;
g(x)与x轴有三个不同的交点即表示函数y=f(x)和函数y=ax有三个不同交点,如图所示:
由图可看出当直线y=ax与曲线f(x)=lnx,x∈[1,3],相切时直线y=ax和曲线y=f(x)有两个公共点;
若直线y=ax再向下旋转便有三个交点,直到y=ax经过曲线y=f(x)的右端点,再向下旋转便成了两个交点;
设切点为(x0,lnx0),∴,又,∴;
∴此时lnx0=1,x0=e;
∴此时a=;
y=f(x)的右端点坐标为(3,ln3);
∴直线y=ax经过右端点时,a=;
∴实数a的取值范围是.
故答案为:[).
【点评】考查通过将定义域转变到已知函数的定义域上求函数解析式的方法,数形结合解题的方法,以及直线和曲线相切时的斜率和曲线在切点处导数的关系.
14.若实数a≥0,b≥1且,则2a+2b+1的取值范围为 [7,9] .
【考点】有理数指数幂的化简求值.
【专题】计算题;转化思想;综合法;函数的性质及应用.
【分析】由已知得(2a﹣1)2=2b(4﹣2b)≥0,从而得到1≤b≤2,由此能求出2a+2b+1的取值范围.
【解答】解:∵实数a≥0,b≥1且,
∴(2a)2+(2b)2=2×2a+4×2b﹣1,
∴(2a﹣1)2=2b(4﹣2b)≥0,
∴4﹣2b≥0,
解得1≤b≤2,∴4≤2b+1≤8,
∵(2a﹣1)2=2b(4﹣2b)≥0,
∴b=1时,2a=3,2a+2b+1=7,
b=2时,2a=1,2a+2b+1=9,
∴7≤2a+2b+1≤9,
∴2a+2b+1的取值范围为[7,9].
故答案为:[7,9].
【点评】本题考查有理数指数幂代数和的取值范围的求法,是基础题,解题时要认真审题,注意有理数指数幂的运算法则的合理运用.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在直角坐标系xOy中,以原点O为圆心作一个单位圆,角α和角β的终边与单位圆分别交于A、B两点,且||=.若0<α<,﹣<β<0,sinβ=﹣.
(1)求△AOB的面积;
(2)求sinα的值.
【考点】余弦定理;正弦定理.
【专题】计算题;转化思想;数形结合法;解三角形;平面向量及应用.
【分析】(1)根据题意设出,,利用向量法则根据﹣表示出,利用向量模的定义列出关系式,整理后利用两角和与差的余弦函数公式即可求出cos(α﹣β)的值,由α与β的范围求出α﹣β的范围,利用同角三角函数间的基本关系求出sin(α﹣β),由三角形面积公式即可得解.
(2)可先求cosβ的值,所求式子变形后,利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值.
【解答】解:(1)根据题意设=(cosα,sinα),=(cosβ,sinβ),
∴=﹣=(cosβ﹣cosα,sinβ﹣sinα),
∴||2=(cosβ﹣cosα)2+(sinβ﹣sinα)2=,即2﹣2(cosβcosα+sinβsinα)=,
∴cos(α﹣β)=cosβcosα+sinβsinα=;
∵0<α<,﹣<β<0,
∴0<α﹣β<π,
∴sin∠AOB=sin(α﹣β)==,
又∵|OA|=1,|OB|=1,
∴S△AOB=|OA| |OB|sin∠AOB==.
(2)∵sinβ=﹣,
∴cosβ==,
则sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ=×﹣×=.
【点评】此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,考查了平面向量的运算,熟练掌握公式是解本题的关键,属于中档题.
16.已知四棱锥S﹣ABCD的底面ABCD是边长为2的正方形,侧面SAB是等边三角形,侧面SCD是以CD为斜边的直角三角形,E为CD的中点,M为SB的中点.
(1)求证:CM∥平面SAE;
(2)求证:SE⊥平面SAB;
(3)求三棱锥S﹣AED的体积.
【考点】直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定.
【专题】计算题;证明题;空间位置关系与距离.
【分析】(1)取SA的中点N,连接MN.△ASB中利用中位线定理,证出MN∥AB且MN=AB,而正方形ABCD中E为CD中点,可得CE∥AB且CE=AB,从而得到CENM为平行四边形,得CM∥EN.最后用线面平行的判定定理,即可证出CM∥平面SAE;
(2)Rt△SCD中,E为斜边中点,可得SE=CD=1.△ESA中算出SE2+SA2=5=AE2,从而得到ES⊥SA,同理△ESB中证出ES⊥SB,结合SA、SB是平面SAB内的相交直线,可证出SE⊥平面SAB.
(3)根据正方形的性质可得S△AED=S△ABE,从而得到VS﹣AED=VS﹣AEB=VE﹣SAB,由(2)得SE是三棱锥E﹣SAB的高,从而算出VE﹣SAB=,由此即可得到VS﹣AED=VE﹣SAB=.
【解答】解:(1)取SA的中点N,连接MN,EN
∵M为SB的中点,N为SA的中点,∴MN∥AB,且MN=AB,
又E是CD的中点,∴CE∥AB,且CE=AB,
∴MN∥CE,且MN=CE,∴四边形CENM为平行四边形,
∴CM∥EN,又EN 平面SAE,CM 平面SAE,
∴CM∥平面SAE.
(2)∵侧面SCD为直角三角形,∠CSD=90°,E为CD的中点,
∴SE=CD=1,
又∵SA=AB=2,AE=,
∴SE2+SA2=5=AE2,可得ES⊥SA,同理可证ES⊥SB,
∵SA∩SB=S,SA、SB 平面SAB,∴SE⊥平面SAB.
(3)根据题意,得VS﹣AED=VS﹣AEB=VE﹣SAB,
∵SE⊥平面SAB,可得SE是三棱锥E﹣SAB的高
∴VE﹣SAB=S△SAB×SE==
因此,三棱锥S﹣AED的体积为VS﹣AED=VE﹣SAB=×=.
【点评】本题在四棱锥中证明线面平行、线面垂直,并求三棱锥的体积.着重考查了空间直线与平面平行的判定定理、直线与平面垂直的判定定理和锥体体积公式等知识,属于中档题.
17.(文科)已知数列{an}的前n项的和为Sn,点P(n,Sn)(n∈N*)在函数f(x)=﹣x2+7x的图象上.
(Ⅰ)求数列{an}的通项公式及Sn的最大值;
(Ⅱ)令bn=(n∈N*),求数列{nbn}的前n项的和Tn;
(Ⅲ)设cn=,数列{cn}的前n项的和为Rn,求使不等式Rn>对一切n∈N*都成立的最大正整数k的值.
【考点】数列的求和;数列的函数特性.
【专题】等差数列与等比数列.
【分析】(1)由于点P(n,Sn)(n∈N)在函数f(x)=﹣x2+7x的图象上.可得Sn.利用当n≥2时,an=Sn﹣Sn﹣1,当n=1时,a1=S1,即可得出an.再利用二次函数的单调性即可得出Sn的最值;
(2)利用“错位相减法”即可得出;
(3)利用“裂项求和”得出Rn,求出其最小值即可.
【解答】解:(1)∵点P(n,Sn)(n∈N)在函数f(x)=﹣x2+7x的图象上.
∴,
当n≥2时,an=Sn﹣Sn﹣1=﹣2n+8
当n=1时,a1=S1=6满足上式,
∴an=﹣2n+8.
又=,且n∈N*
∴当n=3或4时,Sn取得最大值12.
(2)由题意知
∴数列{nbn}的前n项的和为
∴,
相减得,
∴.
(3)由(1)得=
∴=
易知Rn在n∈N*上单调递增,∴Rn的最小值为
不等式对一切n∈N*都成立,则,即k<19.
所以最大正整数k的值为18.
【点评】本题考查了利用“当n≥2时,an=Sn﹣Sn﹣1,当n=1时,a1=S1”得出an、二次函数的单调性、“错位相减法”、“裂项求和”、恒成立问题等基础知识与基本技能方法,属于难题.
18.为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
(1)考虑到农村耕地面积的减少,为节约水资源,要减少水渠的过水量,在原水渠内填土,使其成为横断面为等腰梯形的新水渠,新水渠底面与地面平行(不改变渠宽).问新水渠底宽为多少时,所填土的土方量最少?
(2)考虑到新建果园的灌溉需求,要增大水渠的过水量,现把旧水渠改挖(不能填土)成横断面为等腰梯形的新水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽.
【考点】函数最值的应用.
【专题】应用题;导数的综合应用.
【分析】(1)建立坐标系,设抛物线的方程为x2=2py(p>0).由已知点P(2,2)在抛物线上,推导出抛物线的方程,可得梯形APQB面积,利用导数可得结论.
(2)为了使挖掉的土最少,等腰梯形的两腰必须与抛物线相切,设切点M(t, t2),t>0.则函数在点M的切线方程为y﹣t2=t(x﹣t),由此能推导出设计改挖后的水渠的底宽为m时,可使用权所挖土的土方量最少.
【解答】解:(1)建立如图的坐标系,
设抛物线的方程为x2=2py(p>0).
由已知点P(2,2)在抛物线上,得p=1,
∴抛物线的方程为x2=2y,
设A(t, t2),则此时梯形APQB面积为S(t)=(2t+4)(2﹣t2),
∴S′(t)=﹣,t=,
t∈(0,),S′(t)>0,t∈(,2),S′(t)<0
∴t=,Smax(t)=,
∴新水渠底宽为m时,所填土的土方量最少;
(2)为了使挖掉的土最少,等腰梯形的两腰必须与抛物线相切,
如图,
设切点M(t, t2),t>0.
则函数在点M的切线方程为y﹣t2=t(x﹣t),
令y=0,y=2,得A(t,0),B(,2),
∴此时梯形OABC的面积为S(t)=(t+) 2=t+≥2,
当且仅当t=时,等号成立,
此时|OA|=,
∴设计改挖后的水渠的底宽为m时,土方量最少.
【点评】本题考查函数在生产生活中的实际应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数知识、基本不等式的合理运用.
19.椭圆=1(a>b>0)的离心率为,左焦点F到右准线l的距离为10,圆G:(x﹣1)2+y2=1.
(1)求椭圆的方程;
(2)若P是椭圆上任意一点,过点P作圆G的切线,切点为Q,过点P作右准线l的垂线,垂足为H,求的取值范围;
(3)是否存在以椭圆上的点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)都满足?若存在,请求出圆M的方程;若不存在,请说明理由.
【考点】椭圆的简单性质.
【专题】压轴题;探究型;转化思想;数形结合法;圆锥曲线的定义、性质与方程.
【分析】(1)由题意可得,解方程组得到a,c的值,结合隐含条件求得b,则椭圆方程可求;
(2)圆G:(x﹣1)2+y2=1的圆心在椭圆的右焦点上,把转化为含椭圆离心率与PH的式子,求出PH的范围可得答案;
(3)设圆M:(x﹣m)2+(y﹣n)2=r2(r>0)满足条件,N(x,y),可知点(m,n)满足,化圆的方程为一般式,由得x2+y2﹣6x﹣1=0,
代入圆的方程可得2(m﹣3)x+2ny﹣m2﹣n2﹣1+r2=0对圆M上点N(x,y)恒成立,由系数为0求得m,n,r的值,验证满足后可得答案.
【解答】解:(1)由题意可得,解得a=3,c=1,∴b2=a2﹣c2=8.
则椭圆方程为;
(2)圆G:(x﹣1)2+y2=1的圆心在椭圆的右焦点上,
∴,
∵e=,PH∈[]=[6,12],
∴ [],则∈[];
(3)设圆M:(x﹣m)2+(y﹣n)2=r2(r>0)满足条件,N(x,y),
其中点(m,n)满足,则x2+y2=2mx+2ny﹣m2﹣n2+r2,
,
要使即NF2=2NT2,即x2+y2﹣6x﹣1=0,
代入x2+y2=2mx+2ny﹣m2﹣n2+r2,
得2(m﹣3)x+2ny﹣m2﹣n2﹣1+r2=0对圆M上点N(x,y)恒成立,
只要使,得,经检验m=3,n=0满足,
故存在以椭圆上点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)
都满足,圆M的方程为(x﹣3)2+y2=10.
【点评】本题考查椭圆的简单性质,考查了圆与圆锥曲线的位置关系,对于(3)的求解是该题的难点所在,与恒成立问题进行了交汇,试题设置难度较大.
20.已知函数f(x)=lnx+a(x﹣1)2,其中a∈R.
(1)若f(x)在x=e处的切线斜率为1,求a;
(2)若a>0,g(x)=f(x)﹣x+1,求g(x)在区间[1,2]的最小值;
(3)令h(x)=f(x)﹣ax2,对y=h(x)上任意不同的两点,A(x1,y1),B(x2,y2)直线AB的斜率为k,若x1+x2+k>0恒成立,求实数a的取值范围.
【考点】利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.
【专题】导数的概念及应用;导数的综合应用;不等式的解法及应用.
【分析】(1)求得导数,求出切线的斜率,解方程可得a:
(2)化简g(x),求得导数,讨论当a≥时,当0<a≤时,当<a<时,由单调区间,即可得到最小值;
(3)运用斜率公式,化简整理,即有m(x)=lnx+x2﹣a(2x﹣1)在(0,+∞)上递增,运用导数判断单调性,结合恒成立思想,计算即可得到a的范围.
【解答】解:(1)函数f(x)=lnx+a(x﹣1)2的导数为f′(x)=+2a(x﹣1),
f(x)在x=e处的切线斜率为1,即有+2a(e﹣1)=1,
解得a=;
(2)g(x)=f(x)﹣x+1=lnx+a(x﹣1)2﹣x+1,
g′(x)=+2a(x﹣1)﹣1=,
当a≥时,在[1,2]上g′(x)>0,g(x)递增,
即有x=1处取得最小值,且为0;
当0<a≤时,在[1,2]上g′(x)<0,g(x)递减,
即有x=2处取得最小值,且为ln2+a﹣1;
当<a<时,g(x)在[1,)递减,在(,2)递增,
即有x=处取得最小值,且为﹣ln(2a)+a(﹣1)2﹣+1;
(3)h(x)=f(x)﹣ax2=lnx﹣a(2x﹣1),
x1+x2+k>0恒成立,
即为x1+x2+>0恒成立,
即有>0,
即为m(x)=lnx+x2﹣a(2x﹣1)在(0,+∞)上递增,
即有m′(x)=+2x﹣2a≥0恒成立,
即为2a≤2x+的最小值,
由2x+≥2=2(当且仅当x=,等号成立),
则2a≤2,
解得a≤.
【点评】本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用单调性的定义和构造函数的方法,属于中档题.
同课章节目录
