江苏省徐州市新沂二中2015-2016学年高二(上)第一次月清数学试卷(解析版)
文档属性
| 名称 | 江苏省徐州市新沂二中2015-2016学年高二(上)第一次月清数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 146.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-05 15:56:04 | ||
图片预览




文档简介
2015-2016学年江苏省徐州市新沂二中高二(上)第一次月清数学试卷
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.经过点M(﹣m,3),N(5,﹣m)的直线的斜率为1,则m= .
2.已知直线经过点A(﹣2,0),B(﹣5,3),则该直线的倾斜角为 .
3.已知点A(1,﹣2),B(m,2),且线段AB的垂直平分线的方程是x+2y﹣2=0,则实数m的值是 .
4.梯形ABCD中AB∥CD,AB 平面α,CD 平面α,则直线CD与平面α内的直线的位置关系 .
5.直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,则实数a的值为 .
6.已知一个圆锥的侧面展开图是圆心角为120°的扇形、底面圆的直径为2,则该圆锥的体积为 .
7.过点A(0,2)且倾斜角的正弦值是的直线方程为 .
8.P为△ABC所在平面外一点,O为P在平面ABC上的射影.若PA⊥BC,PB⊥AC,则点O是△ABC的 心.
9.一个体积为8cm3的正方体的顶点都在球面上,则球的表面积是 cm2.
10.如图,在长方体ABCD﹣A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A﹣BB1D1D的体积为 cm3.
11.设α,β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:
①若n⊥β,m∥n,n α,则m∥α;
②若m α,n α,m∥β,n∥β,则α∥β;
③若α∥β,m α,n β,则m∥n;
④若α⊥β,α∩β=m,n α,n⊥m;
其中正确命题的序号为 .
12.如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
其中正确的是 (填序号).
13.若三条直线4x+y+4=0,mx+y+1=0,x﹣y+1=0不能围成三角形,则实数m取值范围是 .
14.已知函数y=的图象与函数y=kx﹣2的图象恰有两个交点,则实数k的取值范围是 .
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
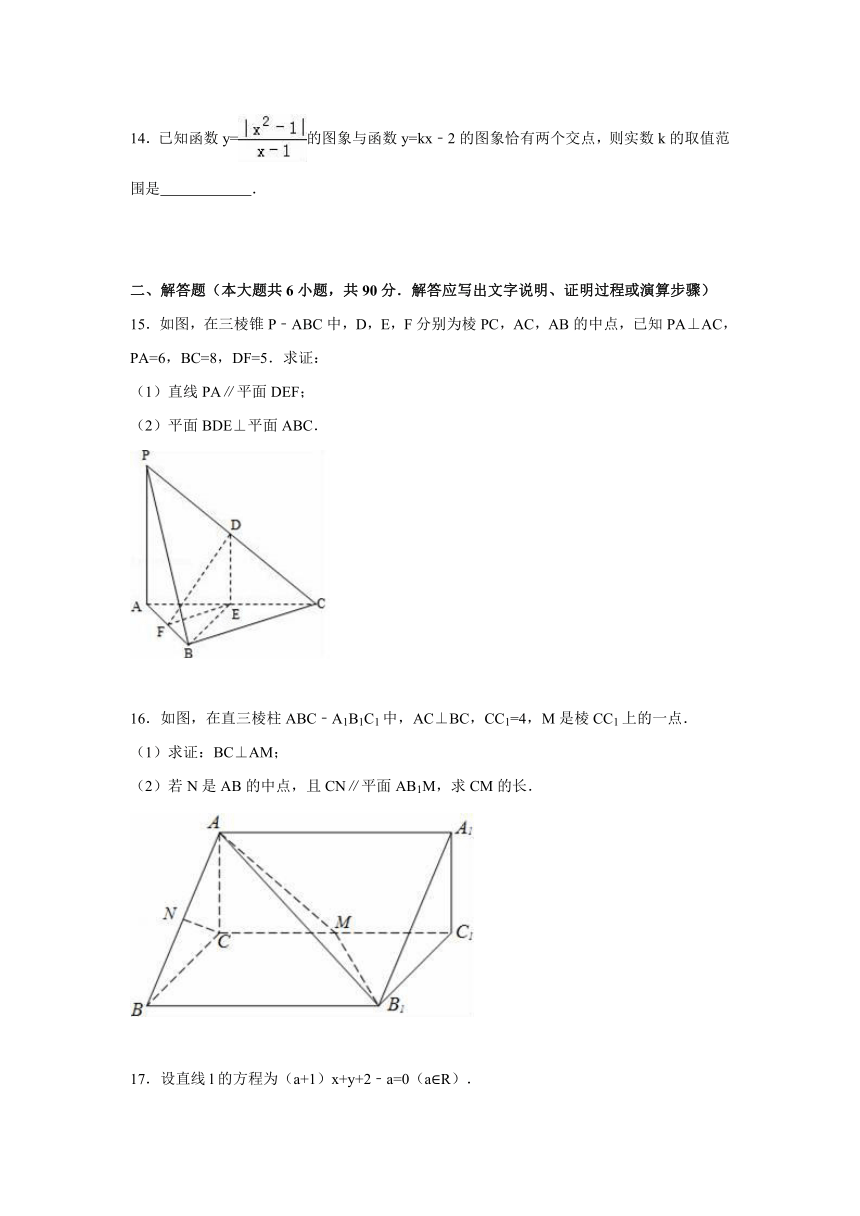
15.如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
16.如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
(1)求证:BC⊥AM;
(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.
17.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
18.△ABC的一个顶点A(2,3),两条高所在直线方程为x﹣2y+3=0和x+y﹣4=0,求△ABC三边所在直线方程.
19.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
(1)求证:DP∥平面ANC;
(2)求证:M是PC中点;
(3)求证:平面PBC⊥平面ADMN.
20.如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF.
2015-2016学年江苏省徐州市新沂二中高二(上)第一次月清数学试卷
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.经过点M(﹣m,3),N(5,﹣m)的直线的斜率为1,则m= ﹣4 .
【考点】直线的斜率.
【专题】直线与圆.
【分析】直接由两点坐标求斜率公式得到关于m的等式,则m可求.
【解答】解:∵M(﹣m,3),N(5,﹣m),
∴,
解得:m=﹣4.
故答案为:﹣4.
【点评】本题考查直线的斜率,训练了由直线上两点的坐标求直线的斜率,是基础题.
2.已知直线经过点A(﹣2,0),B(﹣5,3),则该直线的倾斜角为 145° .
【考点】直线的倾斜角.
【专题】数形结合;综合法;直线与圆.
【分析】由两点的坐标求得直线AB的斜率,再由倾斜角的正切值等于斜率求得倾斜角的值.
【解答】解:由A(﹣2,0),B(﹣5,3),可得
直线AB的斜率k==﹣1.
设直线AB的倾斜角为α(0°≤α<180°),
则tanα=﹣1,α=145°.
故答案为:145°.
【点评】本题考查了直线的倾斜角,考查了直线的倾斜角与斜率的关系,是基础题.
3.已知点A(1,﹣2),B(m,2),且线段AB的垂直平分线的方程是x+2y﹣2=0,则实数m的值是 3 .
【考点】直线的一般式方程与直线的垂直关系.
【专题】直线与圆.
【分析】由题意可得点A、B的中点(,0)在直线x+2y﹣2=0上,代入可得m的方程,解方程可得m的值.
【解答】解:∵线段AB的垂直平分线的方程是x+2y﹣2=0,
∴点A、B的中点(,0)在直线x+2y﹣2=0上,
∴+2×0﹣2=0,解得m=3
故答案为:3.
【点评】本题考查直线的一般式方程,涉及中点坐标公式,属基础题.
4.梯形ABCD中AB∥CD,AB 平面α,CD 平面α,则直线CD与平面α内的直线的位置关系 平行或异面 .
【考点】空间中直线与平面之间的位置关系.
【专题】空间位置关系与距离.
【分析】由线面平行的性质定理,得CD∥α,由此得到直线CD与平面α内的直线的位置关系是平行或异面.
【解答】解:∵AB∥CD,AB 平面α,CD 平面α,
∴由线面平行的性质定理,得CD∥α,
∴直线CD与平面α内的直线的位置关系是平行或异面.
故答案为:平行或异面.
【点评】本题考查直线的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.
5.直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,则实数a的值为 1 .
【考点】直线的一般式方程与直线的平行关系.
【专题】计算题.
【分析】利用两直线平行的条件,一次项系数之比相等,但不等于常数项之比,求得实数a的值.
【解答】解:直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,
∴,解得 a=1.
故答案为 1.
【点评】本题考查两直线平行的条件,利用一次项系数之比相等,但不等于常数项之比,求得实数a的值.
6.已知一个圆锥的侧面展开图是圆心角为120°的扇形、底面圆的直径为2,则该圆锥的体积为 π .
【考点】扇形面积公式;旋转体(圆柱、圆锥、圆台).
【专题】计算题.
【分析】由圆侧面展开图圆心角为120°,列式可解出母线长为3,用勾股定理解出高的值,用圆锥体积公式可算出该圆锥的体积.
【解答】解:设圆锥的高为h,母线为l
则2πr=l,将r=1代入得2π=πl,
∴l=3,可得高h==2
圆锥的体积为V=πr2h=π×12×2=π
故答案为:π
【点评】本题给出圆锥侧面展开图的圆心角和底面直径,求圆锥的体积,着重考查了圆锥的几何特性和锥体体积公式等知识点,属于基础题.
7.过点A(0,2)且倾斜角的正弦值是的直线方程为 3x﹣4y+8=0或3x+4y﹣8=0 .
【考点】直线的倾斜角.
【专题】直线与圆.
【分析】由已知条件推导出斜率k=,由此利用直线过点A(0,2),能求出直线方程.
【解答】解:∵倾斜角α的正弦值是,
∴cosα=±=,
∴斜率k=.
∵直线过点A(0,2),
∴k=时,直线方程为:y﹣2=,即:3x﹣4y+8=0;
k=﹣时,直线方程为:y﹣2=﹣x,即:3x+4y﹣8=0.
∴所求直线方程为:3x﹣4y+8=0或3x+4y﹣8=0.
故答案为:3x﹣4y+8=0或3x+4y﹣8=0.
【点评】本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线斜率的灵活运用.
8.P为△ABC所在平面外一点,O为P在平面ABC上的射影.若PA⊥BC,PB⊥AC,则点O是△ABC的 垂 心.
【考点】三角形五心.
【专题】解三角形.
【分析】由PA⊥BC,PB⊥AC,PO⊥底面ABC,得AO⊥BC,BO⊥AC,由此可得O是△ABC的垂心.
【解答】解:∵P为△ABC所在平面外一点,O为P在平面ABC上的射影,
∴PO⊥面ABC,又BC 面ABC,∴BC⊥PO,
∵PA⊥BC,PA∩PO=P,∴BC⊥平面PAO,
∴AO⊥BC,
∵PO⊥面ABC,又AC 面ABC,∴AC⊥PO,
∵PB⊥AC,PB∩PO=P,∴AC⊥平面PBO,
∴BO⊥AC,
∴O是△ABC的垂心.
故答案为:垂.
【点评】本题考查三角形五心的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.
9.一个体积为8cm3的正方体的顶点都在球面上,则球的表面积是 12π cm2.
【考点】球的体积和表面积.
【专题】计算题.
【分析】先求出球的半径,然后求出球的表面积.
【解答】解:正方体体积为8,可知其边长为2,体对角线为,
即为球的直径,所以半径为,表面积为
【点评】本题考查学生的空间想象能力,以及对公式的考查,是基础题.
10.如图,在长方体ABCD﹣A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A﹣BB1D1D的体积为 6 cm3.
【考点】棱柱、棱锥、棱台的体积.
【专题】空间位置关系与距离;立体几何.
【分析】过A作AO⊥BD于O,求出AO,然后求出几何体的体积即可.
【解答】解:过A作AO⊥BD于O,AO是棱锥的高,所以AO==,
所以四棱锥A﹣BB1D1D的体积为V==6.
故答案为:6.
【点评】本题考查几何体的体积的求法,考查空间想象能力与计算能力.
11.设α,β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:
①若n⊥β,m∥n,n α,则m∥α;
②若m α,n α,m∥β,n∥β,则α∥β;
③若α∥β,m α,n β,则m∥n;
④若α⊥β,α∩β=m,n α,n⊥m;
其中正确命题的序号为 ④ .
【考点】命题的真假判断与应用;空间中直线与平面之间的位置关系.
【专题】空间位置关系与距离.
【分析】利用线面的关系,结合图形逐步判断:①中线面关系,由若n⊥β,m∥n,知m⊥β,则m∥α或m α;
②面面平行的判定定理:一个平面内两条交线和另一平面平行,则这两平面平行;
③线线位置关系考查:相交,平行和异面,由题知不平行;
④线面垂直的判定定理.
【解答】解:①若n⊥β,m∥n,n α,则m∥α或m α,故A错误;
②若m α,n α,m∥β,n∥β,且m,n相交,则α∥β,故B错误;
③若α∥β,m α,n β,则m,n没有交点,所以平行或异面,故C错误;
④若α⊥β,α∩β=m,n α,n⊥m,则n⊥β,故D正确.
故答案为④.
【点评】考查了线面,线线的位置关系,应紧扣定理,性质,不能随意猜测.
12.如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
其中正确的是 ① (填序号).
【考点】直线与平面垂直的判定.
【专题】证明题;空间位置关系与距离.
【分析】根据题意,在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,即SG⊥GE,SG⊥GF,由线面垂直的判定定理,易得SG⊥平面EFG,分析四各个选项,即可给出正确的选择.
【解答】证明:∵在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF,
∴SG⊥平面EFG.
故答案为:①.
【点评】本题主要考查了垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
13.若三条直线4x+y+4=0,mx+y+1=0,x﹣y+1=0不能围成三角形,则实数m取值范围是 {4,1,﹣1} .
【考点】两条直线平行与倾斜角、斜率的关系;两条直线垂直与倾斜角、斜率的关系.
【专题】直线与圆.
【分析】三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x﹣y+1=0不能围成三角形,可得l2∥l1或l2∥l3或l2经过直线l1与l3的交点,解出即可.
【解答】解:由题意,联立,
解得,
∴直线l1与l3的交点为(﹣1,0);
∵三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x﹣y+1=0不能围成三角形,
∴l2∥l1或l2∥l3或l2经过直线l1与l3的交点,
即﹣m=﹣4,或﹣m=1,或﹣m+0+1=0,
解得m=4,或m=±1.
故答案为:{4,1,﹣1}.
【点评】本题考查了相互平行的直线斜率之间的关系、三角形的性质,属于基础题目.
14.已知函数y=的图象与函数y=kx﹣2的图象恰有两个交点,则实数k的取值范围是 (0,1)∪(1,4) .
【考点】根的存在性及根的个数判断.
【专题】函数的性质及应用.
【分析】先化简函数的解析式,在同一个坐标系下画出函数y=的图象与函数y=kx﹣2的图象,结合图象,可得实数k的取值范围.
【解答】解:y===
函数y=kx﹣2的图象恒过点(0,﹣2)
在同一个坐标系下画出函数y=的图象与函数y=kx﹣2的图象
结合图象可实数k的取值范围是(0,1)∪(1,4)
故答案为:(0,1)∪(1,4)
【点评】本题主要考查了根的存在性及根的个数判断,同时考查了作图能力和分类讨论的数学思想,属于基础题.
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
15.如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
【考点】平面与平面垂直的判定;直线与平面垂直的判定.
【专题】空间位置关系与距离;空间角;立体几何.
【分析】(1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可.
【解答】证明:(1)∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA 平面DEF,DE 平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE=PA=3;
又∵E、F为AC、AB的中点,∴EF=BC=4;
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE 平面BDE,∴平面BDE⊥平面ABC.
【点评】本题考查了空间中的平行与垂直问题,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是基础题目.
16.如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
(1)求证:BC⊥AM;
(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.
【考点】直线与平面平行的判定;直线与平面垂直的性质.
【专题】空间位置关系与距离.
【分析】(1)由线面垂直得BC⊥C1C,又BC⊥AC,从而BC⊥平面ACC1A1,由此能证明BC⊥AM.
(2)取AB1的中点P,连接MP,NP,由三角形中位线定理得NP∥BB1,从而得到PNCM是平行四边形,由此能求出CM的长.
【解答】(1)证明:∵ABC﹣A1B1C1为直三棱柱,
∴C1C⊥平面ABC,∴BC⊥C1C,
又BC⊥AC,∴BC⊥平面ACC1A1,
∵AM在平面ACC1A1上,∴BC⊥AM.
(2)解:取AB1的中点P,连接MP,NP,
∵P为AB1中点,N为AB中点,
∴NP为△ABB1的中位线,∴NP∥BB1,
又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,∴MC∥B1B,
∴NP∥CM,∴NPCM共面,
又∵CN∥平面AB1M,∴CNMP,∴PNCM是平行四边形,
∴CM=NP=BB1=CC1=.
【点评】本小题线线平行、直线与平面的平行、线面所成角、探索性问题等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,是中档题.
17.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
【考点】直线的截距式方程;确定直线位置的几何要素;过两条直线交点的直线系方程.
【专题】待定系数法.
【分析】(1)先求出直线l在两坐标轴上的截距,再利用 l在两坐标轴上的截距相等 建立方程,解方程求出a的值,从而得到所求的直线l方程.
(2)把直线l的方程可化为 y=﹣(a+1)x+a﹣2,由题意得,解不等式组求得a的范围.
【解答】解:(1)令x=0,得y=a﹣2. 令y=0,得(a≠﹣1).
∵l在两坐标轴上的截距相等,∴,解之,得a=2或a=0.
∴所求的直线l方程为3x+y=0或x+y+2=0.
(2)直线l的方程可化为 y=﹣(a+1)x+a﹣2.∵l不过第二象限,
∴,∴a≤﹣1.∴a的取值范围为(﹣∞,﹣1].
【点评】本题考查直线在坐标轴上的截距的定义,用待定系数法求直线的方程,以及确定直线位置的几何要素.
18.△ABC的一个顶点A(2,3),两条高所在直线方程为x﹣2y+3=0和x+y﹣4=0,求△ABC三边所在直线方程.
【考点】直线的一般式方程与直线的垂直关系.
【专题】直线与圆.
【分析】不妨设直线x﹣2y+3=0和x+y﹣4=0分别经过点B和点C的高线,由垂直关系可得AB和AC的方程,联立直线方程可得B和C的坐标,可得BC的方程.
【解答】解:不妨设直线x﹣2y+3=0和x+y﹣4=0分别经过点B和点C的高线,
∴由垂直关系可得AB的斜率为1,AC的斜率为﹣2,
∵AB和AC都经过点A(2,3),
∴AB的方程为y﹣3=x﹣2即x﹣y+1=0;
∴AC的方程为y﹣3=﹣2(x﹣2)即2x+y﹣7=0;
联立,解得,即B(1,2),
联立,解得,即C(3,1),
∴BC的斜率为=,
∴BC的方程为y﹣2=﹣(x﹣1),即x+2y﹣5=0.
【点评】本题考查直线的一般式方程和垂直关系,涉及方程组的解集,属基础题.
19.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
(1)求证:DP∥平面ANC;
(2)求证:M是PC中点;
(3)求证:平面PBC⊥平面ADMN.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【专题】证明题.
【分析】(1)接BD,AC,设BD∩AC=O,连接NO,根据菱形的性质及三角形中位线定理,可得PD∥NO,结合线面平行的判定定理即可得到DP∥平面ANC;
(2)由已知易得AD∥BC,则BC∥平面ADMN,由线面平行的性质定理得BC∥MN,根据平行线等分线段定理,即可得到M是PC中点;
(3)取AD中点E,连接PE,BE,BD,由已知中底面ABCD是边长为2的菱形,∠BAD=60°,E为AD的中点,可得BE⊥AD,结合PE⊥AD和线面垂直的判定定理得AD⊥面PBE,由线面垂直的性质可得AD⊥PB,又由等腰三角形PAB中,N为PB的中点,得AN⊥PB,由线面垂直的判定定理得:PB⊥平面ADMN,最后由面面垂直的判定定理得到平面PBC⊥平面ADMN.
【解答】证明:(1)连接BD,AC,设BD∩AC=O,连接NO…
∵ABCD是的菱形∴O是BD中点,又N是PB中点
∴PD∥NO…
又NO 平面ANC,PD 平面ANC…
∴PD∥平面ANC…
(2)依题意有AD∥BC∴BC∥平面ADMN…
而平面PBC∩平面ADMN=MN…
∴BC∥MN…
又N是PB中点∴M是PC中点
(3)取AD中点E,连接PE,BE,BD,
∵ABCD为边长为2的菱形,且∠BAD=60°
∴△ABD为等边三角形,又E为AD的中点
∴BE⊥AD…
又∵PE⊥AD
∴AD⊥面PBE
∴AD⊥PB …
又∵PA=AB,N为PB的中点
∴AN⊥PB…
∴PB⊥平面ADMN而PB 平面PBC…
∴平面PBC⊥平面ADMN…
【点评】本题考查的知识是直线与平面平行的判定,平面与平面垂直的判定,直线与平面平行的性质,(1)的关键是得到PD∥NO,(2)的关键是得到BC∥MN,(3)的关键是线线、线面、面面垂直之间的转化.
20.如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF.
【考点】棱柱、棱锥、棱台的体积;构成空间几何体的基本元素;直线与平面平行的判定.
【专题】综合题;转化思想;综合法;立体几何.
【分析】(1)直接利用体积公式,求三棱锥D﹣ABC的体积;
(2)要证AC⊥平面DEF,先证AC⊥DE,再证AC⊥EF,即可.
(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可.
【解答】(1)解:∵△BCD是正三角形,AB⊥平面BCD,AB=BC=a,
∴三棱锥D﹣ABC的体积V==.
(2)证明:取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF.
(3)解:连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=CM.
当CN=CA时,CF=CN,∴MN∥OF.
∵MN 平面DEF,OF 平面DEF,
∴MN∥平面DEF.
【点评】本题考查棱锥的结构特征,证明线面垂直,线面平行,考查体积的计算,考查逻辑思维能力,是中档题.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.经过点M(﹣m,3),N(5,﹣m)的直线的斜率为1,则m= .
2.已知直线经过点A(﹣2,0),B(﹣5,3),则该直线的倾斜角为 .
3.已知点A(1,﹣2),B(m,2),且线段AB的垂直平分线的方程是x+2y﹣2=0,则实数m的值是 .
4.梯形ABCD中AB∥CD,AB 平面α,CD 平面α,则直线CD与平面α内的直线的位置关系 .
5.直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,则实数a的值为 .
6.已知一个圆锥的侧面展开图是圆心角为120°的扇形、底面圆的直径为2,则该圆锥的体积为 .
7.过点A(0,2)且倾斜角的正弦值是的直线方程为 .
8.P为△ABC所在平面外一点,O为P在平面ABC上的射影.若PA⊥BC,PB⊥AC,则点O是△ABC的 心.
9.一个体积为8cm3的正方体的顶点都在球面上,则球的表面积是 cm2.
10.如图,在长方体ABCD﹣A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A﹣BB1D1D的体积为 cm3.
11.设α,β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:
①若n⊥β,m∥n,n α,则m∥α;
②若m α,n α,m∥β,n∥β,则α∥β;
③若α∥β,m α,n β,则m∥n;
④若α⊥β,α∩β=m,n α,n⊥m;
其中正确命题的序号为 .
12.如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
其中正确的是 (填序号).
13.若三条直线4x+y+4=0,mx+y+1=0,x﹣y+1=0不能围成三角形,则实数m取值范围是 .
14.已知函数y=的图象与函数y=kx﹣2的图象恰有两个交点,则实数k的取值范围是 .
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
15.如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
16.如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
(1)求证:BC⊥AM;
(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.
17.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
18.△ABC的一个顶点A(2,3),两条高所在直线方程为x﹣2y+3=0和x+y﹣4=0,求△ABC三边所在直线方程.
19.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
(1)求证:DP∥平面ANC;
(2)求证:M是PC中点;
(3)求证:平面PBC⊥平面ADMN.
20.如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF.
2015-2016学年江苏省徐州市新沂二中高二(上)第一次月清数学试卷
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.经过点M(﹣m,3),N(5,﹣m)的直线的斜率为1,则m= ﹣4 .
【考点】直线的斜率.
【专题】直线与圆.
【分析】直接由两点坐标求斜率公式得到关于m的等式,则m可求.
【解答】解:∵M(﹣m,3),N(5,﹣m),
∴,
解得:m=﹣4.
故答案为:﹣4.
【点评】本题考查直线的斜率,训练了由直线上两点的坐标求直线的斜率,是基础题.
2.已知直线经过点A(﹣2,0),B(﹣5,3),则该直线的倾斜角为 145° .
【考点】直线的倾斜角.
【专题】数形结合;综合法;直线与圆.
【分析】由两点的坐标求得直线AB的斜率,再由倾斜角的正切值等于斜率求得倾斜角的值.
【解答】解:由A(﹣2,0),B(﹣5,3),可得
直线AB的斜率k==﹣1.
设直线AB的倾斜角为α(0°≤α<180°),
则tanα=﹣1,α=145°.
故答案为:145°.
【点评】本题考查了直线的倾斜角,考查了直线的倾斜角与斜率的关系,是基础题.
3.已知点A(1,﹣2),B(m,2),且线段AB的垂直平分线的方程是x+2y﹣2=0,则实数m的值是 3 .
【考点】直线的一般式方程与直线的垂直关系.
【专题】直线与圆.
【分析】由题意可得点A、B的中点(,0)在直线x+2y﹣2=0上,代入可得m的方程,解方程可得m的值.
【解答】解:∵线段AB的垂直平分线的方程是x+2y﹣2=0,
∴点A、B的中点(,0)在直线x+2y﹣2=0上,
∴+2×0﹣2=0,解得m=3
故答案为:3.
【点评】本题考查直线的一般式方程,涉及中点坐标公式,属基础题.
4.梯形ABCD中AB∥CD,AB 平面α,CD 平面α,则直线CD与平面α内的直线的位置关系 平行或异面 .
【考点】空间中直线与平面之间的位置关系.
【专题】空间位置关系与距离.
【分析】由线面平行的性质定理,得CD∥α,由此得到直线CD与平面α内的直线的位置关系是平行或异面.
【解答】解:∵AB∥CD,AB 平面α,CD 平面α,
∴由线面平行的性质定理,得CD∥α,
∴直线CD与平面α内的直线的位置关系是平行或异面.
故答案为:平行或异面.
【点评】本题考查直线的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.
5.直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,则实数a的值为 1 .
【考点】直线的一般式方程与直线的平行关系.
【专题】计算题.
【分析】利用两直线平行的条件,一次项系数之比相等,但不等于常数项之比,求得实数a的值.
【解答】解:直线ax﹣2y+2=0与直线x+(a﹣3)y+1=0平行,
∴,解得 a=1.
故答案为 1.
【点评】本题考查两直线平行的条件,利用一次项系数之比相等,但不等于常数项之比,求得实数a的值.
6.已知一个圆锥的侧面展开图是圆心角为120°的扇形、底面圆的直径为2,则该圆锥的体积为 π .
【考点】扇形面积公式;旋转体(圆柱、圆锥、圆台).
【专题】计算题.
【分析】由圆侧面展开图圆心角为120°,列式可解出母线长为3,用勾股定理解出高的值,用圆锥体积公式可算出该圆锥的体积.
【解答】解:设圆锥的高为h,母线为l
则2πr=l,将r=1代入得2π=πl,
∴l=3,可得高h==2
圆锥的体积为V=πr2h=π×12×2=π
故答案为:π
【点评】本题给出圆锥侧面展开图的圆心角和底面直径,求圆锥的体积,着重考查了圆锥的几何特性和锥体体积公式等知识点,属于基础题.
7.过点A(0,2)且倾斜角的正弦值是的直线方程为 3x﹣4y+8=0或3x+4y﹣8=0 .
【考点】直线的倾斜角.
【专题】直线与圆.
【分析】由已知条件推导出斜率k=,由此利用直线过点A(0,2),能求出直线方程.
【解答】解:∵倾斜角α的正弦值是,
∴cosα=±=,
∴斜率k=.
∵直线过点A(0,2),
∴k=时,直线方程为:y﹣2=,即:3x﹣4y+8=0;
k=﹣时,直线方程为:y﹣2=﹣x,即:3x+4y﹣8=0.
∴所求直线方程为:3x﹣4y+8=0或3x+4y﹣8=0.
故答案为:3x﹣4y+8=0或3x+4y﹣8=0.
【点评】本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线斜率的灵活运用.
8.P为△ABC所在平面外一点,O为P在平面ABC上的射影.若PA⊥BC,PB⊥AC,则点O是△ABC的 垂 心.
【考点】三角形五心.
【专题】解三角形.
【分析】由PA⊥BC,PB⊥AC,PO⊥底面ABC,得AO⊥BC,BO⊥AC,由此可得O是△ABC的垂心.
【解答】解:∵P为△ABC所在平面外一点,O为P在平面ABC上的射影,
∴PO⊥面ABC,又BC 面ABC,∴BC⊥PO,
∵PA⊥BC,PA∩PO=P,∴BC⊥平面PAO,
∴AO⊥BC,
∵PO⊥面ABC,又AC 面ABC,∴AC⊥PO,
∵PB⊥AC,PB∩PO=P,∴AC⊥平面PBO,
∴BO⊥AC,
∴O是△ABC的垂心.
故答案为:垂.
【点评】本题考查三角形五心的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.
9.一个体积为8cm3的正方体的顶点都在球面上,则球的表面积是 12π cm2.
【考点】球的体积和表面积.
【专题】计算题.
【分析】先求出球的半径,然后求出球的表面积.
【解答】解:正方体体积为8,可知其边长为2,体对角线为,
即为球的直径,所以半径为,表面积为
【点评】本题考查学生的空间想象能力,以及对公式的考查,是基础题.
10.如图,在长方体ABCD﹣A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A﹣BB1D1D的体积为 6 cm3.
【考点】棱柱、棱锥、棱台的体积.
【专题】空间位置关系与距离;立体几何.
【分析】过A作AO⊥BD于O,求出AO,然后求出几何体的体积即可.
【解答】解:过A作AO⊥BD于O,AO是棱锥的高,所以AO==,
所以四棱锥A﹣BB1D1D的体积为V==6.
故答案为:6.
【点评】本题考查几何体的体积的求法,考查空间想象能力与计算能力.
11.设α,β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:
①若n⊥β,m∥n,n α,则m∥α;
②若m α,n α,m∥β,n∥β,则α∥β;
③若α∥β,m α,n β,则m∥n;
④若α⊥β,α∩β=m,n α,n⊥m;
其中正确命题的序号为 ④ .
【考点】命题的真假判断与应用;空间中直线与平面之间的位置关系.
【专题】空间位置关系与距离.
【分析】利用线面的关系,结合图形逐步判断:①中线面关系,由若n⊥β,m∥n,知m⊥β,则m∥α或m α;
②面面平行的判定定理:一个平面内两条交线和另一平面平行,则这两平面平行;
③线线位置关系考查:相交,平行和异面,由题知不平行;
④线面垂直的判定定理.
【解答】解:①若n⊥β,m∥n,n α,则m∥α或m α,故A错误;
②若m α,n α,m∥β,n∥β,且m,n相交,则α∥β,故B错误;
③若α∥β,m α,n β,则m,n没有交点,所以平行或异面,故C错误;
④若α⊥β,α∩β=m,n α,n⊥m,则n⊥β,故D正确.
故答案为④.
【点评】考查了线面,线线的位置关系,应紧扣定理,性质,不能随意猜测.
12.如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
其中正确的是 ① (填序号).
【考点】直线与平面垂直的判定.
【专题】证明题;空间位置关系与距离.
【分析】根据题意,在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,即SG⊥GE,SG⊥GF,由线面垂直的判定定理,易得SG⊥平面EFG,分析四各个选项,即可给出正确的选择.
【解答】证明:∵在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF,
∴SG⊥平面EFG.
故答案为:①.
【点评】本题主要考查了垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
13.若三条直线4x+y+4=0,mx+y+1=0,x﹣y+1=0不能围成三角形,则实数m取值范围是 {4,1,﹣1} .
【考点】两条直线平行与倾斜角、斜率的关系;两条直线垂直与倾斜角、斜率的关系.
【专题】直线与圆.
【分析】三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x﹣y+1=0不能围成三角形,可得l2∥l1或l2∥l3或l2经过直线l1与l3的交点,解出即可.
【解答】解:由题意,联立,
解得,
∴直线l1与l3的交点为(﹣1,0);
∵三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x﹣y+1=0不能围成三角形,
∴l2∥l1或l2∥l3或l2经过直线l1与l3的交点,
即﹣m=﹣4,或﹣m=1,或﹣m+0+1=0,
解得m=4,或m=±1.
故答案为:{4,1,﹣1}.
【点评】本题考查了相互平行的直线斜率之间的关系、三角形的性质,属于基础题目.
14.已知函数y=的图象与函数y=kx﹣2的图象恰有两个交点,则实数k的取值范围是 (0,1)∪(1,4) .
【考点】根的存在性及根的个数判断.
【专题】函数的性质及应用.
【分析】先化简函数的解析式,在同一个坐标系下画出函数y=的图象与函数y=kx﹣2的图象,结合图象,可得实数k的取值范围.
【解答】解:y===
函数y=kx﹣2的图象恒过点(0,﹣2)
在同一个坐标系下画出函数y=的图象与函数y=kx﹣2的图象
结合图象可实数k的取值范围是(0,1)∪(1,4)
故答案为:(0,1)∪(1,4)
【点评】本题主要考查了根的存在性及根的个数判断,同时考查了作图能力和分类讨论的数学思想,属于基础题.
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
15.如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
【考点】平面与平面垂直的判定;直线与平面垂直的判定.
【专题】空间位置关系与距离;空间角;立体几何.
【分析】(1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可.
【解答】证明:(1)∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA 平面DEF,DE 平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE=PA=3;
又∵E、F为AC、AB的中点,∴EF=BC=4;
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE 平面BDE,∴平面BDE⊥平面ABC.
【点评】本题考查了空间中的平行与垂直问题,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是基础题目.
16.如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
(1)求证:BC⊥AM;
(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.
【考点】直线与平面平行的判定;直线与平面垂直的性质.
【专题】空间位置关系与距离.
【分析】(1)由线面垂直得BC⊥C1C,又BC⊥AC,从而BC⊥平面ACC1A1,由此能证明BC⊥AM.
(2)取AB1的中点P,连接MP,NP,由三角形中位线定理得NP∥BB1,从而得到PNCM是平行四边形,由此能求出CM的长.
【解答】(1)证明:∵ABC﹣A1B1C1为直三棱柱,
∴C1C⊥平面ABC,∴BC⊥C1C,
又BC⊥AC,∴BC⊥平面ACC1A1,
∵AM在平面ACC1A1上,∴BC⊥AM.
(2)解:取AB1的中点P,连接MP,NP,
∵P为AB1中点,N为AB中点,
∴NP为△ABB1的中位线,∴NP∥BB1,
又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,∴MC∥B1B,
∴NP∥CM,∴NPCM共面,
又∵CN∥平面AB1M,∴CNMP,∴PNCM是平行四边形,
∴CM=NP=BB1=CC1=.
【点评】本小题线线平行、直线与平面的平行、线面所成角、探索性问题等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,是中档题.
17.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
【考点】直线的截距式方程;确定直线位置的几何要素;过两条直线交点的直线系方程.
【专题】待定系数法.
【分析】(1)先求出直线l在两坐标轴上的截距,再利用 l在两坐标轴上的截距相等 建立方程,解方程求出a的值,从而得到所求的直线l方程.
(2)把直线l的方程可化为 y=﹣(a+1)x+a﹣2,由题意得,解不等式组求得a的范围.
【解答】解:(1)令x=0,得y=a﹣2. 令y=0,得(a≠﹣1).
∵l在两坐标轴上的截距相等,∴,解之,得a=2或a=0.
∴所求的直线l方程为3x+y=0或x+y+2=0.
(2)直线l的方程可化为 y=﹣(a+1)x+a﹣2.∵l不过第二象限,
∴,∴a≤﹣1.∴a的取值范围为(﹣∞,﹣1].
【点评】本题考查直线在坐标轴上的截距的定义,用待定系数法求直线的方程,以及确定直线位置的几何要素.
18.△ABC的一个顶点A(2,3),两条高所在直线方程为x﹣2y+3=0和x+y﹣4=0,求△ABC三边所在直线方程.
【考点】直线的一般式方程与直线的垂直关系.
【专题】直线与圆.
【分析】不妨设直线x﹣2y+3=0和x+y﹣4=0分别经过点B和点C的高线,由垂直关系可得AB和AC的方程,联立直线方程可得B和C的坐标,可得BC的方程.
【解答】解:不妨设直线x﹣2y+3=0和x+y﹣4=0分别经过点B和点C的高线,
∴由垂直关系可得AB的斜率为1,AC的斜率为﹣2,
∵AB和AC都经过点A(2,3),
∴AB的方程为y﹣3=x﹣2即x﹣y+1=0;
∴AC的方程为y﹣3=﹣2(x﹣2)即2x+y﹣7=0;
联立,解得,即B(1,2),
联立,解得,即C(3,1),
∴BC的斜率为=,
∴BC的方程为y﹣2=﹣(x﹣1),即x+2y﹣5=0.
【点评】本题考查直线的一般式方程和垂直关系,涉及方程组的解集,属基础题.
19.如图,在四棱锥P﹣ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
(1)求证:DP∥平面ANC;
(2)求证:M是PC中点;
(3)求证:平面PBC⊥平面ADMN.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【专题】证明题.
【分析】(1)接BD,AC,设BD∩AC=O,连接NO,根据菱形的性质及三角形中位线定理,可得PD∥NO,结合线面平行的判定定理即可得到DP∥平面ANC;
(2)由已知易得AD∥BC,则BC∥平面ADMN,由线面平行的性质定理得BC∥MN,根据平行线等分线段定理,即可得到M是PC中点;
(3)取AD中点E,连接PE,BE,BD,由已知中底面ABCD是边长为2的菱形,∠BAD=60°,E为AD的中点,可得BE⊥AD,结合PE⊥AD和线面垂直的判定定理得AD⊥面PBE,由线面垂直的性质可得AD⊥PB,又由等腰三角形PAB中,N为PB的中点,得AN⊥PB,由线面垂直的判定定理得:PB⊥平面ADMN,最后由面面垂直的判定定理得到平面PBC⊥平面ADMN.
【解答】证明:(1)连接BD,AC,设BD∩AC=O,连接NO…
∵ABCD是的菱形∴O是BD中点,又N是PB中点
∴PD∥NO…
又NO 平面ANC,PD 平面ANC…
∴PD∥平面ANC…
(2)依题意有AD∥BC∴BC∥平面ADMN…
而平面PBC∩平面ADMN=MN…
∴BC∥MN…
又N是PB中点∴M是PC中点
(3)取AD中点E,连接PE,BE,BD,
∵ABCD为边长为2的菱形,且∠BAD=60°
∴△ABD为等边三角形,又E为AD的中点
∴BE⊥AD…
又∵PE⊥AD
∴AD⊥面PBE
∴AD⊥PB …
又∵PA=AB,N为PB的中点
∴AN⊥PB…
∴PB⊥平面ADMN而PB 平面PBC…
∴平面PBC⊥平面ADMN…
【点评】本题考查的知识是直线与平面平行的判定,平面与平面垂直的判定,直线与平面平行的性质,(1)的关键是得到PD∥NO,(2)的关键是得到BC∥MN,(3)的关键是线线、线面、面面垂直之间的转化.
20.如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF.
【考点】棱柱、棱锥、棱台的体积;构成空间几何体的基本元素;直线与平面平行的判定.
【专题】综合题;转化思想;综合法;立体几何.
【分析】(1)直接利用体积公式,求三棱锥D﹣ABC的体积;
(2)要证AC⊥平面DEF,先证AC⊥DE,再证AC⊥EF,即可.
(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可.
【解答】(1)解:∵△BCD是正三角形,AB⊥平面BCD,AB=BC=a,
∴三棱锥D﹣ABC的体积V==.
(2)证明:取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF.
(3)解:连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=CM.
当CN=CA时,CF=CN,∴MN∥OF.
∵MN 平面DEF,OF 平面DEF,
∴MN∥平面DEF.
【点评】本题考查棱锥的结构特征,证明线面垂直,线面平行,考查体积的计算,考查逻辑思维能力,是中档题.
同课章节目录
