青岛版(六三制)数学八年级上册 5.3几何证明举例 第五课时 课件(共13张PPT)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 5.3几何证明举例 第五课时 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 19:08:52 | ||
图片预览



文档简介
(共13张PPT)
第五课时
几何证明举例
复习导入
现在你有几种判定直角三角形全等的方法?
1.边角边 简称 “SAS”
2.角边角 简称 “ASA”
3.边边边 简称 “SSS”
4.角角边 简称 “AAS”
教学目标
1.根据三角形全等推导“HL”定理;
2.熟练应用“斜边、直角边”定理。
一、预习诊断
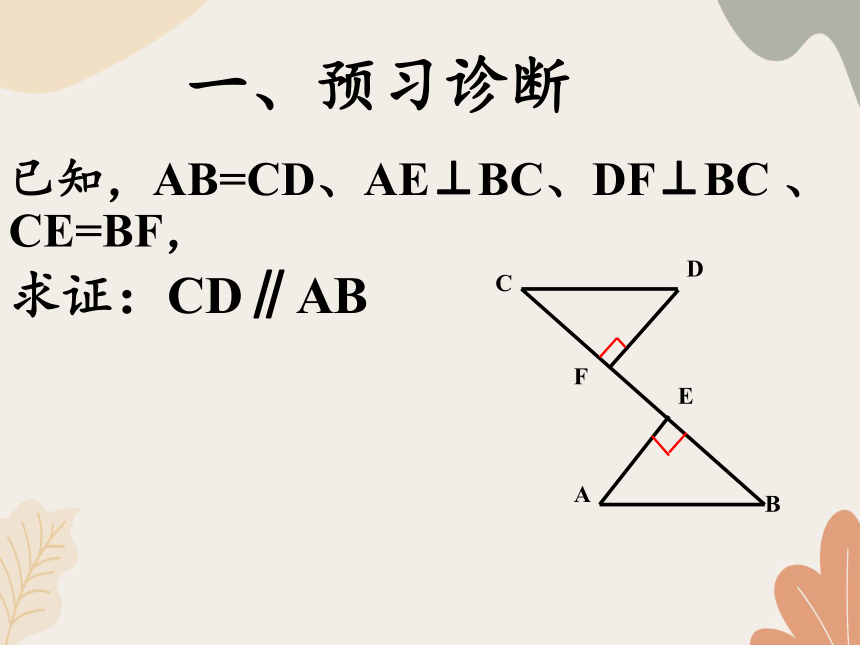
已知,AB=CD、AE⊥BC、DF⊥BC 、CE=BF,
求证:CD∥AB
C
D
A
B
F
E
二、精讲点拨
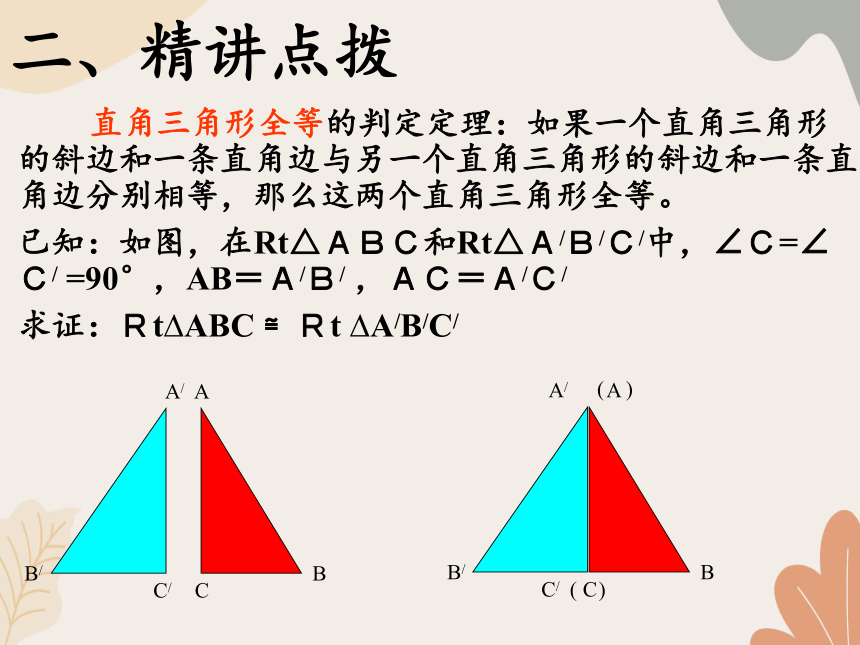
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等。
已知:如图,在Rt△ABC和Rt△A/B/C/中,∠C=∠C/ =90°,AB=A/B/ ,AC=A/C/
求证:Rt ABC ≌Rt A/B/C/
A/
B/
C/
A
C
B
A/
B/
C/
A
C
B
( )
( )
C/
A(A/)
B(B/)
C
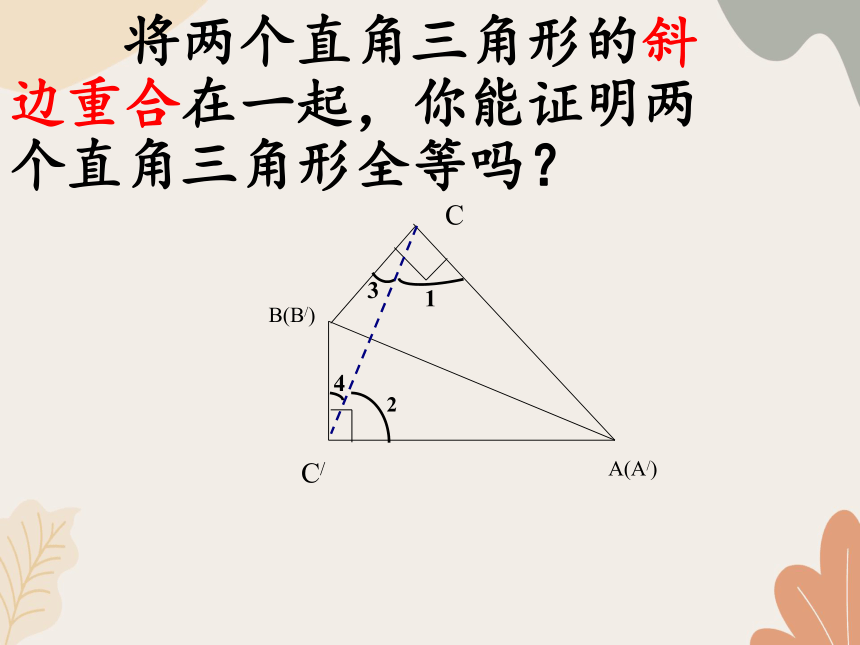
将两个直角三角形的斜边重合在一起,你能证明两个直角三角形全等吗?
4
3
1
2
SSA翻身啦!
由于HL定理的存在,在直角三角形中,两边及一角分别相等的两个三角形,当其中较大一边的对角是直角时,它们全等。
“斜边、直角边”或“HL” 定理的符号语言
在Rt ABC和Rt DEF中
AB=DE
AC=DF
∴ Rt ABC ≌ Rt DEF (HL)
∵
典型例题
例1.如图,在 △ABC 中,BD=CD,DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,
求证:△ABC是等腰三角形。
随堂练习
如图:已知AC=BD,
∠C=∠D=90°,
求证:(1)Rt ABC≌Rt BAD
A
B
D
C
O
例2.已知一直角边和斜边作直角三角形
(1) 作直线DE,在直线DE上任取一点C,过点C作射CM⊥DE
(2)在射线CM上截取线段CB=a;
(3) 以B为圆心,c为半径画弧,交射线CE于点A;
(4) 连接AB。
△ABC就是所求作的三角形。
知:线段a,c,求作Rt ABC,使直角边BC=a,斜边AB=c
D
M
C
E
C
M
E
B
D
C
M
E
B
D
A
C
M
E
B
A
D
a
c
三、系统总结
1.应用斜边直角边(HL)定理判定两个三角形全等,要按照定理的条件,准确地找出“对应相等”的边;
2.寻找使结论成立所需要的条件时,要注意充分利用图形中的隐含条件,如“公共边、公共角、对顶角等等”;
3.要认真掌握证明两个三角形全等的推理模式。
谢 谢
第五课时
几何证明举例
复习导入
现在你有几种判定直角三角形全等的方法?
1.边角边 简称 “SAS”
2.角边角 简称 “ASA”
3.边边边 简称 “SSS”
4.角角边 简称 “AAS”
教学目标
1.根据三角形全等推导“HL”定理;
2.熟练应用“斜边、直角边”定理。
一、预习诊断
已知,AB=CD、AE⊥BC、DF⊥BC 、CE=BF,
求证:CD∥AB
C
D
A
B
F
E
二、精讲点拨
直角三角形全等的判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等。
已知:如图,在Rt△ABC和Rt△A/B/C/中,∠C=∠C/ =90°,AB=A/B/ ,AC=A/C/
求证:Rt ABC ≌Rt A/B/C/
A/
B/
C/
A
C
B
A/
B/
C/
A
C
B
( )
( )
C/
A(A/)
B(B/)
C
将两个直角三角形的斜边重合在一起,你能证明两个直角三角形全等吗?
4
3
1
2
SSA翻身啦!
由于HL定理的存在,在直角三角形中,两边及一角分别相等的两个三角形,当其中较大一边的对角是直角时,它们全等。
“斜边、直角边”或“HL” 定理的符号语言
在Rt ABC和Rt DEF中
AB=DE
AC=DF
∴ Rt ABC ≌ Rt DEF (HL)
∵
典型例题
例1.如图,在 △ABC 中,BD=CD,DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,
求证:△ABC是等腰三角形。
随堂练习
如图:已知AC=BD,
∠C=∠D=90°,
求证:(1)Rt ABC≌Rt BAD
A
B
D
C
O
例2.已知一直角边和斜边作直角三角形
(1) 作直线DE,在直线DE上任取一点C,过点C作射CM⊥DE
(2)在射线CM上截取线段CB=a;
(3) 以B为圆心,c为半径画弧,交射线CE于点A;
(4) 连接AB。
△ABC就是所求作的三角形。
知:线段a,c,求作Rt ABC,使直角边BC=a,斜边AB=c
D
M
C
E
C
M
E
B
D
C
M
E
B
D
A
C
M
E
B
A
D
a
c
三、系统总结
1.应用斜边直角边(HL)定理判定两个三角形全等,要按照定理的条件,准确地找出“对应相等”的边;
2.寻找使结论成立所需要的条件时,要注意充分利用图形中的隐含条件,如“公共边、公共角、对顶角等等”;
3.要认真掌握证明两个三角形全等的推理模式。
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
