湖北省恩施市崔坝中学2024-2025学年上学期八年级期中数学试题卷(含答案)
文档属性
| 名称 | 湖北省恩施市崔坝中学2024-2025学年上学期八年级期中数学试题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 20:17:32 | ||
图片预览



文档简介
2024-2025学年八年级数学上学期期中试题卷
第一部分(选择题 共30分)
选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.下列长度的三条线段能首尾相接构成三角形的是( )
A.1,2,3 B.3,4,5 C.4,5,10 D.6,9,2
2.第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行,中国取得金牌榜第一名的好成绩,如图所示巴黎奥运会项目图标中,是轴对称图形的是( )
A. B.
C. D.
3.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
4.如图,将一副三角尺按图中所示位置摆放,点C在FD的延长线上,点C、F分别为直角顶点,且∠A=60°,∠E=45°,若AB∥CF,则∠CBD的度数是( )
A.15° B.20° C.25° D.30°
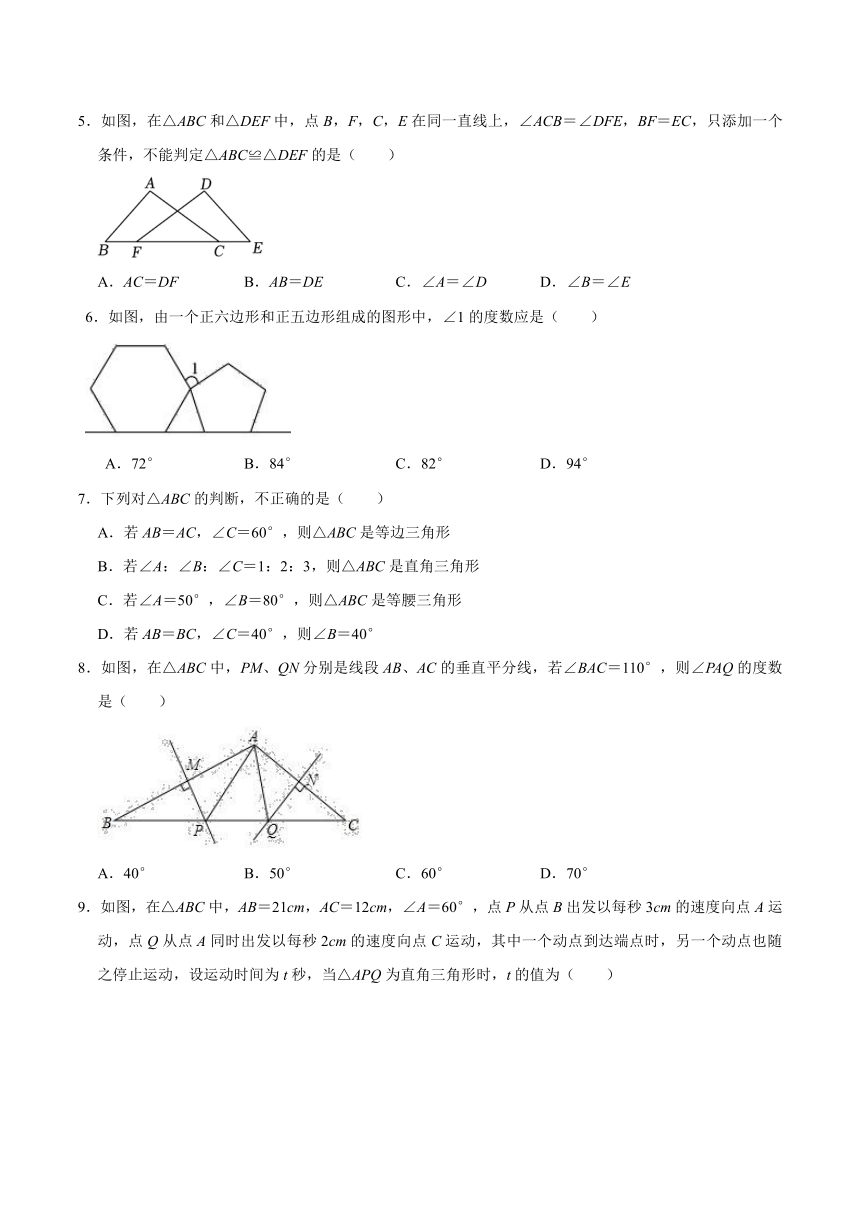
5.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,∠ACB=∠DFE,BF=EC,只添加一个条件,不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
6.如图,由一个正六边形和正五边形组成的图形中,∠1的度数应是( )
A.72° B.84° C.82° D.94°
7.下列对△ABC的判断,不正确的是( )
A.若AB=AC,∠C=60°,则△ABC是等边三角形
B.若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.若∠A=50°,∠B=80°,则△ABC是等腰三角形
D.若AB=BC,∠C=40°,则∠B=40°
8.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40° B.50° C.60° D.70°
9.如图,在△ABC中,AB=21cm,AC=12cm,∠A=60°,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒,当△APQ为直角三角形时,t的值为( )
A.2.5秒 B.3秒 C.3或秒 D.2.5或3秒
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
第二部分(非选择题 共90分)
二、填空题(本大题共5小题,每小题3分,满分15分)
11.已知等腰三角形的周长为18,其中一边长为5,则该等腰三角形的底边长为 .
12.如图,在△ABC中,AB=BE,AD=DE.若∠A=70°,∠C=50°,则∠EDC= °.
13.如图,BC、AE是锐角△ABF的高,相交于点D,若AD=BF,AF=7,CF=2,则BD的长为 .
14.将△ABC按如图所示翻折,DE为折痕,若∠A+∠B=130°,则∠1+∠2= °.
15.如图,等腰三角形ABC的面积为24,底边BC=6,腰AC的垂直平分线EF分别交边AC、AB于E、F两点,点M为线段EF上一动点,点D为BC的中点,连接CM、DM.在点M的运动过程中,△CDM的周长存在最小值为 .
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(6分)如图,已知AE∥CF,AB=CD,∠ADF=∠CBE.求证:△ABE≌△CDA.
17.(7分)如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠C=70°.
(1)求∠AOB的度数;
(2)若∠ABC=50°,求∠DAE的度数.
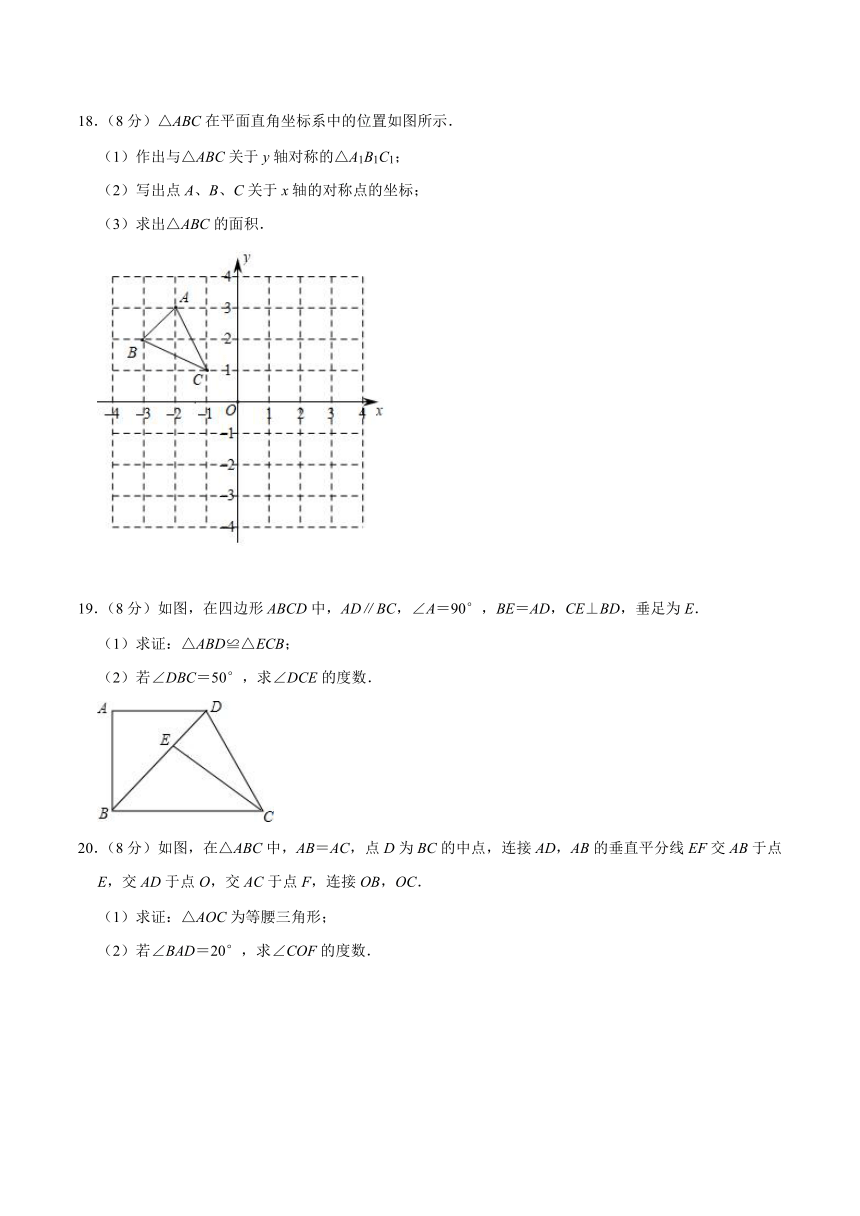
18.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)作出与△ABC关于y轴对称的△A1B1C1;
(2)写出点A、B、C关于x轴的对称点的坐标;
(3)求出△ABC的面积.
19.(8分)如图,在四边形ABCD中,AD∥BC,∠A=90°,BE=AD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
20.(8分)如图,在△ABC中,AB=AC,点D为BC的中点,连接AD,AB的垂直平分线EF交AB于点E,交AD于点O,交AC于点F,连接OB,OC.
(1)求证:△AOC为等腰三角形;
(2)若∠BAD=20°,求∠COF的度数.
21.(8分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
22.(8分)在等边三角形ABC中,点E在AB边上,点D在CB的延长线上,且DE=EC.
(1)如图1,当E为AB中点时,求证:CB=2BD;
(2)如图2,若AB=12,AE=2,求CD的长.
23.(10分)小明在学习过程中,对教材中的一个有趣问题做如图探究:
(1)【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(2)【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,若∠B=40°,求∠CEF和∠CFE的度数;
(3)【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M,若∠M=35°,求∠CFE的度数.
24.(12分)如图,△ABC是等腰直角三角形,AB=BC,直角顶点B在x轴上,一锐角顶点C在y轴上.
(1)如图1,若点B的坐标是(﹣2,0),点A的坐标是(3,2),求点C的坐标.
(2)如图2,若y轴恰好平分∠ACB,AB与y轴交于点D,过点A作AE⊥y轴于点E,问CD与AE有怎样的数量关系?并说明理由.
(3)如图3,直角边BC的两个端点在两坐标轴上滑动,使点A在第二象限内,过点A作AF⊥y轴于点F,在滑动的过程中,为定值,求出这个定值.
参考答案
选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
B C D A B B D A C D
二、填空题(本大题共5小题,每小题3分,共15分)
11.8或5 12.20° 13.3
14.100 15.11
三、解答题:本大题共9小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(6分)
【解答】证明:∵AE∥CF,
∴∠BAE=∠C,
∵∠ADF=∠CBE,
∴180°﹣∠ADF=180°﹣∠CBE,即∠ADC=∠EBA,
又∵AB=CD,
在△ABE和△CDA中,
,
∴△ABE≌△CDA(ASA).
17.(7分)
【解答】解:(1)∵AE、BF是∠BAC、∠ABC的角平分线,
∴,
在△ABC中,∠C=70°,
∴∠BAC+∠ABC=180°﹣∠C=110°,
∴;
(2)∵在△ABC中,AD是高,∠C=70°,∠ABC=50°,
∴∠DAC=90°﹣∠C=90°﹣70°=20°,∠BAC=180°﹣∠ABC﹣∠C=60°
∵AE是∠BAC的角平分线,
∴,
∴∠DAE=∠CAE﹣∠CAD=30°﹣20°=10°,
∴∠DAE=10°.
18.(8分)
【解答】解:(1)如图所示,△A1B1C1即为所求. ……………………2分
(2)如图所示,A2(﹣2,﹣3),B2(﹣3,﹣2),C2(﹣1,﹣1); ……………………5分
(3)△ABC的面积为2×21×21×21×1. ……………………8分
19.(8分)
【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,
∴△ABD≌△ECB(ASA); ……………………4分
(2)解:∵△ABD≌△ECB,
∴BC=BD,
∵∠DBC=50°,
∴∠EDC(180°﹣50°)=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCE=90°﹣∠EDC=90°﹣65°=25°. ……………………8分
20.(8分)
【解答】(1)证明:∵EF是AB的中垂线,
∴OA=OB,
∵AB=AC,D为BC中点,
∴AD⊥BC,
∴AD是BC的中垂线,
∴OB=OC,
∴OA=OC,
∴△OAC是等腰三角形. ……………………4分
(2)解:∵AB=AC,D为BC中点,
∴∠DAC=∠BAD=20°,
∴∠BAC=40°,
∵EF是AB的中垂线,
∴EF⊥AB,
∴∠AFE=50°,
∵OA=OC,
∴∠OCA=∠OAC=20°,
∵∠AFE=∠OCA+∠COF,
∴50°=20°+∠COF,
∴∠COF=30°. ……………………8分
21.(8分)
【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB; ……………………4分
(2)解:AB=AF+2BE, ……………………5分
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE. ……………………8分
22.(8分)
【解答】解:(1)∵△ABC为等边三角形,
∴∠ABC=∠A=∠ACB=60°,
∵EB=AE,
∴CE⊥AB,CE是∠ACB的角平分线,
∴∠BEC=90°,∠BCE=30°,
∴2EB=BC,
∵ED=EC,
∴∠EDC=∠ECD=30°,
∴∠DEB=60°﹣30°=30°,
∴BD=BE,
∴BC=2BD; ……………………4分
(2)如图2,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
∴CD=BC+BD=12+2=14. ……………………8分
23.(10分)
【解答】(1)证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE; ……………………3分
(2)解:∵∠B=40°,∠ACB=90°,
∴∠GAB=∠B+∠ACB=40°+90°=130°,
∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF130°=65°,
∵CD为AB边上的高,
∴∠ADF=∠ACE=90°,
∴∠CFE=90°﹣∠GAF=90°﹣65°=25°, ……………………5分
又∵∠CAE=∠GAF=65°,∠ACB=90°,
∴∠CEF=90°﹣∠CAE=90°﹣65°=25°; ……………………7分
(3)证明:∵C、A、G三点共线,AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
∴∠CFE=90°﹣∠M=90°﹣35°=55°. ……………………10分
24.(12分)
【解答】解:(1)如图1,过点A作AN⊥x轴于点N,
则∠ANB=∠BOC=90°,
∴∠ABN+∠BAN=90°,
∵△ABC是等腰直角三角形,AB=BC,
∴∠ABN+∠CBO=∠ABC=90°,
∴∠BAN=∠CBO,
在△BAN和△CBO中,
,
∴△BAN≌△CBO(AAS),
∴BN=CO,
∵点B的坐标是(﹣2,0),点A的坐标是(3,2),
∴BN=2+3=5,
∴CO=5,
∴点C的坐标为(0,﹣5), ……………………4分
(2)CD与AE的数量关系为:CD=2AE,理由如下: ……………………5分
如图2,延长AE交CB的延长线于点G,
∵y轴平分∠ACB,AE⊥y,
∴△ACG是等腰三角形,∠AED=90°,
∴AE=GEAG,∠GAB+∠ADE=90°,
∵△ABC是等腰直角三角形,AB=BC,
∴∠CBD=∠ABG=90°,∴
∠DCB+∠CDB=90°,
∵∠ADE=∠CDB,
∴∠GAB=∠DCB,
在△GAB和△DCB中,
,
∴△GAB≌△DCB(ASA),
∴AG=CD,
∴AECD,
∴CD=2AE; ……………………8分
(3)如图3,过点A作AH⊥OB于点H,
则∠AHB=∠AHO=90°,
∵AF⊥y轴,
∴四边形AHOF是矩形,
∴OH=AF,
∵∠ABH+∠CBO=90°,∠CBO+∠BCO=90°,
∴∠ABH=∠BCO,
在△ABH和△BCO中,
,
∴△ABH≌△BCO(AAS),
∴HB=OC,
∵HB=OB﹣OH=OB﹣AF,
∴OC=OB﹣AF,
∴1. ……………………12分
第一部分(选择题 共30分)
选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.下列长度的三条线段能首尾相接构成三角形的是( )
A.1,2,3 B.3,4,5 C.4,5,10 D.6,9,2
2.第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行,中国取得金牌榜第一名的好成绩,如图所示巴黎奥运会项目图标中,是轴对称图形的是( )
A. B.
C. D.
3.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm C.4cm D.3cm
4.如图,将一副三角尺按图中所示位置摆放,点C在FD的延长线上,点C、F分别为直角顶点,且∠A=60°,∠E=45°,若AB∥CF,则∠CBD的度数是( )
A.15° B.20° C.25° D.30°
5.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,∠ACB=∠DFE,BF=EC,只添加一个条件,不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
6.如图,由一个正六边形和正五边形组成的图形中,∠1的度数应是( )
A.72° B.84° C.82° D.94°
7.下列对△ABC的判断,不正确的是( )
A.若AB=AC,∠C=60°,则△ABC是等边三角形
B.若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.若∠A=50°,∠B=80°,则△ABC是等腰三角形
D.若AB=BC,∠C=40°,则∠B=40°
8.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40° B.50° C.60° D.70°
9.如图,在△ABC中,AB=21cm,AC=12cm,∠A=60°,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒,当△APQ为直角三角形时,t的值为( )
A.2.5秒 B.3秒 C.3或秒 D.2.5或3秒
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
第二部分(非选择题 共90分)
二、填空题(本大题共5小题,每小题3分,满分15分)
11.已知等腰三角形的周长为18,其中一边长为5,则该等腰三角形的底边长为 .
12.如图,在△ABC中,AB=BE,AD=DE.若∠A=70°,∠C=50°,则∠EDC= °.
13.如图,BC、AE是锐角△ABF的高,相交于点D,若AD=BF,AF=7,CF=2,则BD的长为 .
14.将△ABC按如图所示翻折,DE为折痕,若∠A+∠B=130°,则∠1+∠2= °.
15.如图,等腰三角形ABC的面积为24,底边BC=6,腰AC的垂直平分线EF分别交边AC、AB于E、F两点,点M为线段EF上一动点,点D为BC的中点,连接CM、DM.在点M的运动过程中,△CDM的周长存在最小值为 .
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(6分)如图,已知AE∥CF,AB=CD,∠ADF=∠CBE.求证:△ABE≌△CDA.
17.(7分)如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠C=70°.
(1)求∠AOB的度数;
(2)若∠ABC=50°,求∠DAE的度数.
18.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)作出与△ABC关于y轴对称的△A1B1C1;
(2)写出点A、B、C关于x轴的对称点的坐标;
(3)求出△ABC的面积.
19.(8分)如图,在四边形ABCD中,AD∥BC,∠A=90°,BE=AD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
20.(8分)如图,在△ABC中,AB=AC,点D为BC的中点,连接AD,AB的垂直平分线EF交AB于点E,交AD于点O,交AC于点F,连接OB,OC.
(1)求证:△AOC为等腰三角形;
(2)若∠BAD=20°,求∠COF的度数.
21.(8分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
22.(8分)在等边三角形ABC中,点E在AB边上,点D在CB的延长线上,且DE=EC.
(1)如图1,当E为AB中点时,求证:CB=2BD;
(2)如图2,若AB=12,AE=2,求CD的长.
23.(10分)小明在学习过程中,对教材中的一个有趣问题做如图探究:
(1)【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(2)【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,若∠B=40°,求∠CEF和∠CFE的度数;
(3)【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M,若∠M=35°,求∠CFE的度数.
24.(12分)如图,△ABC是等腰直角三角形,AB=BC,直角顶点B在x轴上,一锐角顶点C在y轴上.
(1)如图1,若点B的坐标是(﹣2,0),点A的坐标是(3,2),求点C的坐标.
(2)如图2,若y轴恰好平分∠ACB,AB与y轴交于点D,过点A作AE⊥y轴于点E,问CD与AE有怎样的数量关系?并说明理由.
(3)如图3,直角边BC的两个端点在两坐标轴上滑动,使点A在第二象限内,过点A作AF⊥y轴于点F,在滑动的过程中,为定值,求出这个定值.
参考答案
选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
B C D A B B D A C D
二、填空题(本大题共5小题,每小题3分,共15分)
11.8或5 12.20° 13.3
14.100 15.11
三、解答题:本大题共9小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(6分)
【解答】证明:∵AE∥CF,
∴∠BAE=∠C,
∵∠ADF=∠CBE,
∴180°﹣∠ADF=180°﹣∠CBE,即∠ADC=∠EBA,
又∵AB=CD,
在△ABE和△CDA中,
,
∴△ABE≌△CDA(ASA).
17.(7分)
【解答】解:(1)∵AE、BF是∠BAC、∠ABC的角平分线,
∴,
在△ABC中,∠C=70°,
∴∠BAC+∠ABC=180°﹣∠C=110°,
∴;
(2)∵在△ABC中,AD是高,∠C=70°,∠ABC=50°,
∴∠DAC=90°﹣∠C=90°﹣70°=20°,∠BAC=180°﹣∠ABC﹣∠C=60°
∵AE是∠BAC的角平分线,
∴,
∴∠DAE=∠CAE﹣∠CAD=30°﹣20°=10°,
∴∠DAE=10°.
18.(8分)
【解答】解:(1)如图所示,△A1B1C1即为所求. ……………………2分
(2)如图所示,A2(﹣2,﹣3),B2(﹣3,﹣2),C2(﹣1,﹣1); ……………………5分
(3)△ABC的面积为2×21×21×21×1. ……………………8分
19.(8分)
【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,
∴△ABD≌△ECB(ASA); ……………………4分
(2)解:∵△ABD≌△ECB,
∴BC=BD,
∵∠DBC=50°,
∴∠EDC(180°﹣50°)=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCE=90°﹣∠EDC=90°﹣65°=25°. ……………………8分
20.(8分)
【解答】(1)证明:∵EF是AB的中垂线,
∴OA=OB,
∵AB=AC,D为BC中点,
∴AD⊥BC,
∴AD是BC的中垂线,
∴OB=OC,
∴OA=OC,
∴△OAC是等腰三角形. ……………………4分
(2)解:∵AB=AC,D为BC中点,
∴∠DAC=∠BAD=20°,
∴∠BAC=40°,
∵EF是AB的中垂线,
∴EF⊥AB,
∴∠AFE=50°,
∵OA=OC,
∴∠OCA=∠OAC=20°,
∵∠AFE=∠OCA+∠COF,
∴50°=20°+∠COF,
∴∠COF=30°. ……………………8分
21.(8分)
【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB; ……………………4分
(2)解:AB=AF+2BE, ……………………5分
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE. ……………………8分
22.(8分)
【解答】解:(1)∵△ABC为等边三角形,
∴∠ABC=∠A=∠ACB=60°,
∵EB=AE,
∴CE⊥AB,CE是∠ACB的角平分线,
∴∠BEC=90°,∠BCE=30°,
∴2EB=BC,
∵ED=EC,
∴∠EDC=∠ECD=30°,
∴∠DEB=60°﹣30°=30°,
∴BD=BE,
∴BC=2BD; ……………………4分
(2)如图2,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
∴CD=BC+BD=12+2=14. ……………………8分
23.(10分)
【解答】(1)证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE; ……………………3分
(2)解:∵∠B=40°,∠ACB=90°,
∴∠GAB=∠B+∠ACB=40°+90°=130°,
∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF130°=65°,
∵CD为AB边上的高,
∴∠ADF=∠ACE=90°,
∴∠CFE=90°﹣∠GAF=90°﹣65°=25°, ……………………5分
又∵∠CAE=∠GAF=65°,∠ACB=90°,
∴∠CEF=90°﹣∠CAE=90°﹣65°=25°; ……………………7分
(3)证明:∵C、A、G三点共线,AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
∴∠CFE=90°﹣∠M=90°﹣35°=55°. ……………………10分
24.(12分)
【解答】解:(1)如图1,过点A作AN⊥x轴于点N,
则∠ANB=∠BOC=90°,
∴∠ABN+∠BAN=90°,
∵△ABC是等腰直角三角形,AB=BC,
∴∠ABN+∠CBO=∠ABC=90°,
∴∠BAN=∠CBO,
在△BAN和△CBO中,
,
∴△BAN≌△CBO(AAS),
∴BN=CO,
∵点B的坐标是(﹣2,0),点A的坐标是(3,2),
∴BN=2+3=5,
∴CO=5,
∴点C的坐标为(0,﹣5), ……………………4分
(2)CD与AE的数量关系为:CD=2AE,理由如下: ……………………5分
如图2,延长AE交CB的延长线于点G,
∵y轴平分∠ACB,AE⊥y,
∴△ACG是等腰三角形,∠AED=90°,
∴AE=GEAG,∠GAB+∠ADE=90°,
∵△ABC是等腰直角三角形,AB=BC,
∴∠CBD=∠ABG=90°,∴
∠DCB+∠CDB=90°,
∵∠ADE=∠CDB,
∴∠GAB=∠DCB,
在△GAB和△DCB中,
,
∴△GAB≌△DCB(ASA),
∴AG=CD,
∴AECD,
∴CD=2AE; ……………………8分
(3)如图3,过点A作AH⊥OB于点H,
则∠AHB=∠AHO=90°,
∵AF⊥y轴,
∴四边形AHOF是矩形,
∴OH=AF,
∵∠ABH+∠CBO=90°,∠CBO+∠BCO=90°,
∴∠ABH=∠BCO,
在△ABH和△BCO中,
,
∴△ABH≌△BCO(AAS),
∴HB=OC,
∵HB=OB﹣OH=OB﹣AF,
∴OC=OB﹣AF,
∴1. ……………………12分
同课章节目录
