数学六年级下人教版6.1比和比例课件
文档属性
| 名称 | 数学六年级下人教版6.1比和比例课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 573.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-04 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
1.数与代数
比和比例
整理和复习
一、引入情境,回顾旧知
提问1:谁能用“比的知识”说说男同学、女同学、全班人数的关系?
预设:
男生人数和女生人数的比是 ( )。
女生人数和男生人数的比是 ( )。
男生人数和全班人数的比是 ( )。
女生人数和全班人数的比是 ( )。
全班人数和男生人数的比是 ( )。
全班人数和女生人数的比是 ( )。
监控:比的顺序。
教师板书
一、引入情境,回顾旧知
提问2:黑板上写了这么多的比,谁能再说一个比和黑板上的比,
组成比例?
监控:比值相等。
教师板书
监控问题:
①说的对吗?
②你是怎么判断的?
③判断的依据是什么?
二、梳理旧知,探寻联系
﹙二﹚汇报交流
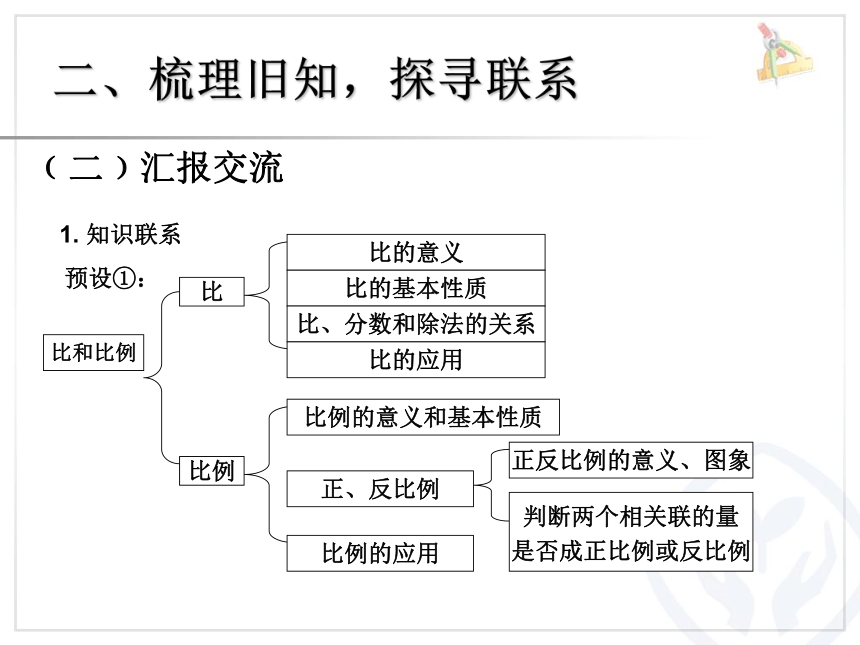
1. 知识联系
预设①:
比
比例
比的意义
比的基本性质
比、分数和除法的关系
比的应用
比例的意义和基本性质
正、反比例
比例的应用
正反比例的意义、图象
判断两个相关联的量
是否成正比例或反比例
比和比例
﹙二﹚汇报交流
二、梳理旧知,探寻联系
1. 知识联系
预设②:
比例
比例应用
反比例意义
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
正比例意义
比例的基本性质
解比例
正比例意义
反比例意义
1. 知识联系
﹙二﹚汇报交流
二、梳理旧知,探寻联系
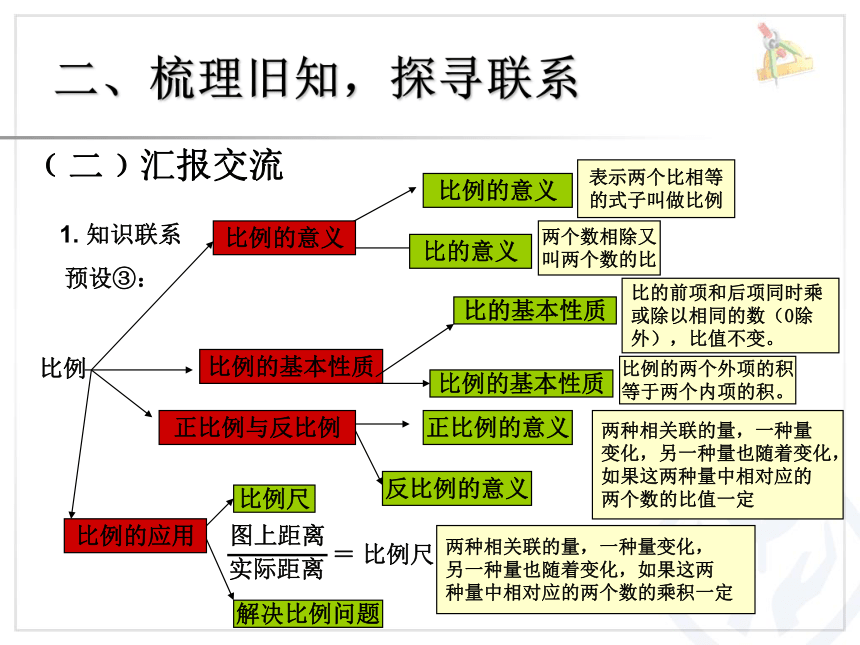
预设③:
比例
比例的意义
比的意义
比例的意义
比例的基本性质
比的基本性质
比例的基本性质
两个数相除又
叫两个数的比
比例的两个外项的积
等于两个内项的积。
正比例与反比例
正比例的意义
反比例的意义
两种相关联的量,一种量
变化,另一种量也随着变化,
如果这两种量中相对应的
两个数的比值一定
两种相关联的量,一种量变化,
另一种量也随着变化,如果这两
种量中相对应的两个数的乘积一定
表示两个比相等
的式子叫做比例
比例的应用
比例尺
解决比例问题
实际距离
图上距离
= 比例尺
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
二、梳理旧知,探寻联系
合作要求:
①先在小组内说说这部分知识之间的联系与区别。
②用自己喜欢的方式,在题纸上把这部分知识写一写。
﹙例如:画图表……﹚
﹙一﹚提出合作要求
出示信息:
1. 知识联系
﹙二﹚汇报交流
二、梳理旧知,探寻联系
监控:
①比和比例有什么联系?
②有无遗漏知识点
③个性化表扬
提问3:说说你们组是怎么抓住知识内在联系进行整理的。
二、梳理旧知,探寻联系
﹙二﹚汇报交流
2. 知识区别
在比例里,两个内项的
积等于两个外项的积。
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
基 本
性 质
0.4 ∶ 0.8 = 1.2 ∶ 2.4
3 ∶ 2 = 1.5
前项 后项 比值
各部分
名 称
表示两个比相等的式子叫做比例。
两个数的比表示两个数相除。
意义
比例
比
內项
外项
小结:刚才同学们从知识内在联系和区别两方面梳理了比和比例的知识。
想必大家又有了新的收获。
提问4:比、比例的基本性质有什么用途呢?
预设:
①比的基本性质可以帮助我们把比化成最简单的整数比。
②比例的基本性质可以帮助我们解比例。
二、梳理旧知,探寻联系
﹙二﹚汇报交流
出示练习:
化简比:
解比例:
3
2
2∶
7
2
4
1
∶x = ∶2
二、梳理旧知,探寻联系
﹙三﹚比、分数、除法的关系
提问5:比和分数、除法有什么联系?又有什么区别呢?
请大家在小组内讨论交流,之后填写下面表格。
联系 例子
各部分名称
分数
除法
比
二、梳理旧知,探寻联系
﹙三﹚比、分数、除法的关系
预设:
比
分数
除法
前项
分子
被除数
∶(比号)
(分数线)
÷(除号)
后项
分母
除数
比值
分数值
商
监控问题:
①你们看出来它们之间的联系了吗?谁相当于谁呢?
②可不可以从基本性质的角度进行分析呢?
(1)甲车4小时行驶280km,乙车3小时行驶300km。
①甲车行驶的路程与时间的比是( )。
②乙车行驶的路程与时间的比是( )。
③乙车与甲车行驶的路程比是( )。
④甲车与乙车行驶的时间比是( )。
(2)如果n×4=m×7,那么n:m=( ):( )。
二、梳理旧知,探寻联系
出示练习:
﹙四﹚正比例和反比例
二、梳理旧知,探寻联系
出示信息:
提问6:请你判断上面各题中的两种量是否成比例。
如果成比例,成什么比例?
1.《小学生作文》的单价一定,订阅的费用与订阅的数量。
2. 圆柱体积一定,圆柱的底面积与高。
3. 一个人的身高与他的年龄。
4. 小麦每公顷产量一定,小麦的总产量与公顷数。
5. 书的总页数一定,未读的页数与已读的页数。
6. 书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
二、梳理旧知,探寻联系
﹙四﹚正比例和反比例
监控:说说你判断的理由。
预设:
正比例: 1、4。
反比例: 2、6。
不成比例:3、5。
预设:
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的
关系叫做正比例关系。
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的
关系叫做反比例关系。
二、梳理旧知,探寻联系
﹙四﹚正比例和反比例
提问7:谁再结合例子,说说什么是正比例?什么是反比例?
提问8:如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),
正比例关系可以怎样表示?
提问9:如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以怎样表示?
预设:
预设:xy=k
=k
y
x
三、巩固练习
1. 大小两个圆的半径之比是3:5。它们的直径之比是( ),
面积之比是( )。
2. 在一个比例中,两个内项互为倒数,一个外项是1.5,
另一个外项是( )。
3. 圆的面积与圆的半径成( )。
A. 正比例 B. 反比例 C. 不成比例 D. 无法判断
4. 在比例里,两个外项的积一定,两个内项成( )。
A. 正比例 B. 反比例 C. 不成比例 D. 无法判断
四、布置作业
作业:第85页练习十七, 第1题、第2题。
1.数与代数
比和比例
整理和复习
一、引入情境,回顾旧知
提问1:谁能用“比的知识”说说男同学、女同学、全班人数的关系?
预设:
男生人数和女生人数的比是 ( )。
女生人数和男生人数的比是 ( )。
男生人数和全班人数的比是 ( )。
女生人数和全班人数的比是 ( )。
全班人数和男生人数的比是 ( )。
全班人数和女生人数的比是 ( )。
监控:比的顺序。
教师板书
一、引入情境,回顾旧知
提问2:黑板上写了这么多的比,谁能再说一个比和黑板上的比,
组成比例?
监控:比值相等。
教师板书
监控问题:
①说的对吗?
②你是怎么判断的?
③判断的依据是什么?
二、梳理旧知,探寻联系
﹙二﹚汇报交流
1. 知识联系
预设①:
比
比例
比的意义
比的基本性质
比、分数和除法的关系
比的应用
比例的意义和基本性质
正、反比例
比例的应用
正反比例的意义、图象
判断两个相关联的量
是否成正比例或反比例
比和比例
﹙二﹚汇报交流
二、梳理旧知,探寻联系
1. 知识联系
预设②:
比例
比例应用
反比例意义
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
正比例意义
比例的基本性质
解比例
正比例意义
反比例意义
1. 知识联系
﹙二﹚汇报交流
二、梳理旧知,探寻联系
预设③:
比例
比例的意义
比的意义
比例的意义
比例的基本性质
比的基本性质
比例的基本性质
两个数相除又
叫两个数的比
比例的两个外项的积
等于两个内项的积。
正比例与反比例
正比例的意义
反比例的意义
两种相关联的量,一种量
变化,另一种量也随着变化,
如果这两种量中相对应的
两个数的比值一定
两种相关联的量,一种量变化,
另一种量也随着变化,如果这两
种量中相对应的两个数的乘积一定
表示两个比相等
的式子叫做比例
比例的应用
比例尺
解决比例问题
实际距离
图上距离
= 比例尺
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
二、梳理旧知,探寻联系
合作要求:
①先在小组内说说这部分知识之间的联系与区别。
②用自己喜欢的方式,在题纸上把这部分知识写一写。
﹙例如:画图表……﹚
﹙一﹚提出合作要求
出示信息:
1. 知识联系
﹙二﹚汇报交流
二、梳理旧知,探寻联系
监控:
①比和比例有什么联系?
②有无遗漏知识点
③个性化表扬
提问3:说说你们组是怎么抓住知识内在联系进行整理的。
二、梳理旧知,探寻联系
﹙二﹚汇报交流
2. 知识区别
在比例里,两个内项的
积等于两个外项的积。
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
基 本
性 质
0.4 ∶ 0.8 = 1.2 ∶ 2.4
3 ∶ 2 = 1.5
前项 后项 比值
各部分
名 称
表示两个比相等的式子叫做比例。
两个数的比表示两个数相除。
意义
比例
比
內项
外项
小结:刚才同学们从知识内在联系和区别两方面梳理了比和比例的知识。
想必大家又有了新的收获。
提问4:比、比例的基本性质有什么用途呢?
预设:
①比的基本性质可以帮助我们把比化成最简单的整数比。
②比例的基本性质可以帮助我们解比例。
二、梳理旧知,探寻联系
﹙二﹚汇报交流
出示练习:
化简比:
解比例:
3
2
2∶
7
2
4
1
∶x = ∶2
二、梳理旧知,探寻联系
﹙三﹚比、分数、除法的关系
提问5:比和分数、除法有什么联系?又有什么区别呢?
请大家在小组内讨论交流,之后填写下面表格。
联系 例子
各部分名称
分数
除法
比
二、梳理旧知,探寻联系
﹙三﹚比、分数、除法的关系
预设:
比
分数
除法
前项
分子
被除数
∶(比号)
(分数线)
÷(除号)
后项
分母
除数
比值
分数值
商
监控问题:
①你们看出来它们之间的联系了吗?谁相当于谁呢?
②可不可以从基本性质的角度进行分析呢?
(1)甲车4小时行驶280km,乙车3小时行驶300km。
①甲车行驶的路程与时间的比是( )。
②乙车行驶的路程与时间的比是( )。
③乙车与甲车行驶的路程比是( )。
④甲车与乙车行驶的时间比是( )。
(2)如果n×4=m×7,那么n:m=( ):( )。
二、梳理旧知,探寻联系
出示练习:
﹙四﹚正比例和反比例
二、梳理旧知,探寻联系
出示信息:
提问6:请你判断上面各题中的两种量是否成比例。
如果成比例,成什么比例?
1.《小学生作文》的单价一定,订阅的费用与订阅的数量。
2. 圆柱体积一定,圆柱的底面积与高。
3. 一个人的身高与他的年龄。
4. 小麦每公顷产量一定,小麦的总产量与公顷数。
5. 书的总页数一定,未读的页数与已读的页数。
6. 书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
二、梳理旧知,探寻联系
﹙四﹚正比例和反比例
监控:说说你判断的理由。
预设:
正比例: 1、4。
反比例: 2、6。
不成比例:3、5。
预设:
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的
关系叫做正比例关系。
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的
关系叫做反比例关系。
二、梳理旧知,探寻联系
﹙四﹚正比例和反比例
提问7:谁再结合例子,说说什么是正比例?什么是反比例?
提问8:如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),
正比例关系可以怎样表示?
提问9:如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以怎样表示?
预设:
预设:xy=k
=k
y
x
三、巩固练习
1. 大小两个圆的半径之比是3:5。它们的直径之比是( ),
面积之比是( )。
2. 在一个比例中,两个内项互为倒数,一个外项是1.5,
另一个外项是( )。
3. 圆的面积与圆的半径成( )。
A. 正比例 B. 反比例 C. 不成比例 D. 无法判断
4. 在比例里,两个外项的积一定,两个内项成( )。
A. 正比例 B. 反比例 C. 不成比例 D. 无法判断
四、布置作业
作业:第85页练习十七, 第1题、第2题。
