第12章 第4课时 证明(3) 同步练习(含答案)
文档属性
| 名称 | 第12章 第4课时 证明(3) 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 35.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-04 00:00:00 | ||
图片预览

文档简介
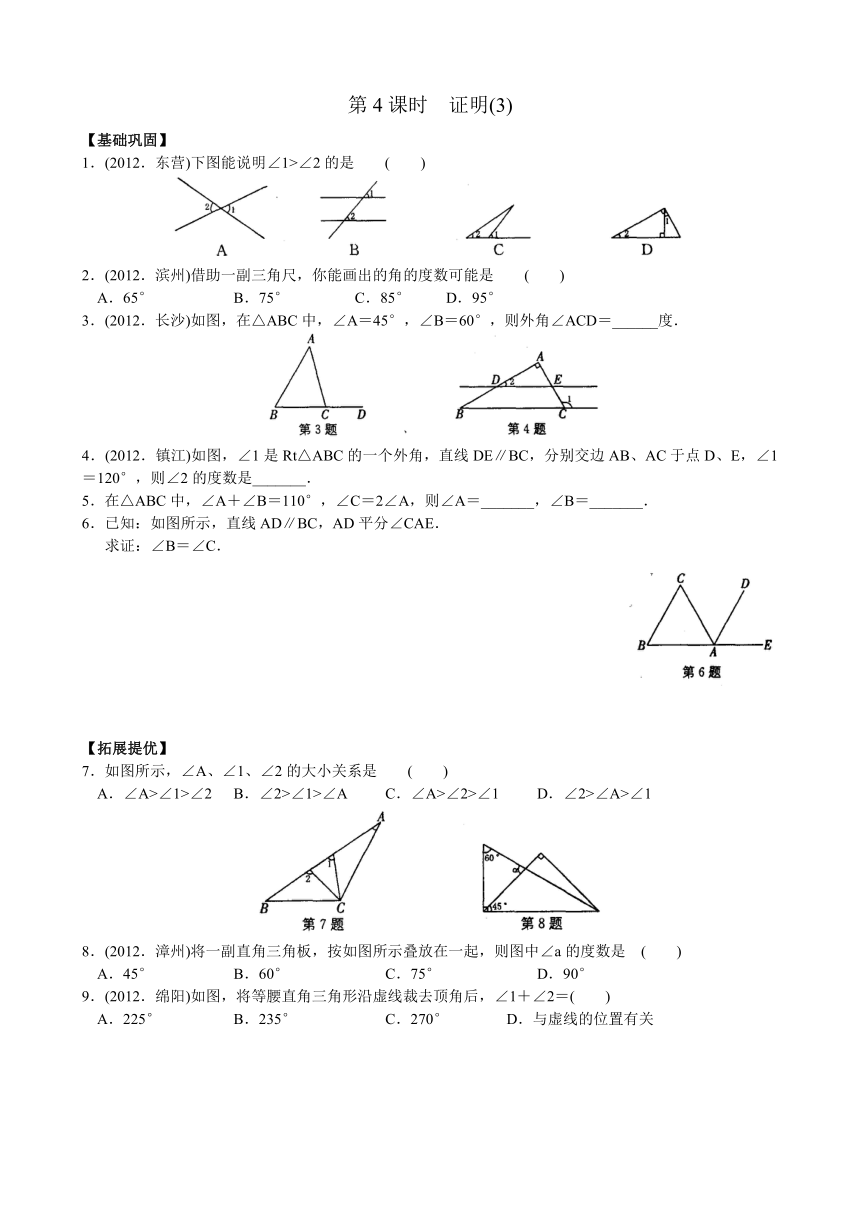
第4课时 证明(3)
【基础巩固】
1.(2012.东营)下图能说明∠1>∠2的是 ( )
2.(2012.滨州)借助一副三角尺,你能画出的角的度数可能是 ( )
A.65° B.75° C.85° D.95°
3.(2012.长沙)如图,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD=______度.
4.(2012.镇江)如图,∠1是Rt△ABC的一个外角,直线DE∥BC,分别交边AB、AC于点D、E,∠1=120°,则∠2的度数是_______.
5.在△ABC中,∠A+∠B=110°,∠C=2∠A,则∠A=_______,∠B=_______.
6.已知:如图所示,直线AD∥BC,AD平分∠CAE.
求证:∠B=∠C.
【拓展提优】
7.如图所示,∠A、∠1、∠2的大小关系是 ( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A C.∠A>∠2>∠1 D.∠2>∠A>∠1
8.(2012.漳州)将一副直角三角板,按如图所示叠放在一起,则图中∠a的度数是 ( )
A.45° B.60° C.75° D.90°
9.(2012.绵阳)如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
A.225° B.235° C.270° D.与虚线的位置有关
10.(2012.鞍山)如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是_______.
11.(2012.呼和浩特)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______.
12.已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC(_______),
∴∠2=_______(______________).
∵∠1=∠2(已知),
∴∠1=∠_______(等量代换),
∴EF∥CD(_______),
∴∠AEF=∠_______(______________).
∵EF⊥AB(已知).
∴∠AEF=90°(_______),
∴∠ADC=90°(_______),
∴CD⊥AB(_______).
13.已知:如图,D是△ABC内的任意一点.求证:∠BDC=∠1+∠A+∠2.
14.如图AB∥DE,∠1=∠2,问AE与DC的位置关系,说明理由.
参考答案
1.C 2.B 3.105 4.30°5.35° 75° 6.略
7.B 8.C 9.C 10.25° 11.66.5°
12.同位角相等,两直线平行∠ACD 两直线平行,内错角相等 ∠ACD 同位角相等,两直线平行 ∠ADC 两直线平行,同位角相等 垂直定义 等量代换 垂直定义 13.略
14.AE∥DC
【基础巩固】
1.(2012.东营)下图能说明∠1>∠2的是 ( )
2.(2012.滨州)借助一副三角尺,你能画出的角的度数可能是 ( )
A.65° B.75° C.85° D.95°
3.(2012.长沙)如图,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD=______度.
4.(2012.镇江)如图,∠1是Rt△ABC的一个外角,直线DE∥BC,分别交边AB、AC于点D、E,∠1=120°,则∠2的度数是_______.
5.在△ABC中,∠A+∠B=110°,∠C=2∠A,则∠A=_______,∠B=_______.
6.已知:如图所示,直线AD∥BC,AD平分∠CAE.
求证:∠B=∠C.
【拓展提优】
7.如图所示,∠A、∠1、∠2的大小关系是 ( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A C.∠A>∠2>∠1 D.∠2>∠A>∠1
8.(2012.漳州)将一副直角三角板,按如图所示叠放在一起,则图中∠a的度数是 ( )
A.45° B.60° C.75° D.90°
9.(2012.绵阳)如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=( )
A.225° B.235° C.270° D.与虚线的位置有关
10.(2012.鞍山)如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是_______.
11.(2012.呼和浩特)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______.
12.已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC(_______),
∴∠2=_______(______________).
∵∠1=∠2(已知),
∴∠1=∠_______(等量代换),
∴EF∥CD(_______),
∴∠AEF=∠_______(______________).
∵EF⊥AB(已知).
∴∠AEF=90°(_______),
∴∠ADC=90°(_______),
∴CD⊥AB(_______).
13.已知:如图,D是△ABC内的任意一点.求证:∠BDC=∠1+∠A+∠2.
14.如图AB∥DE,∠1=∠2,问AE与DC的位置关系,说明理由.
参考答案
1.C 2.B 3.105 4.30°5.35° 75° 6.略
7.B 8.C 9.C 10.25° 11.66.5°
12.同位角相等,两直线平行∠ACD 两直线平行,内错角相等 ∠ACD 同位角相等,两直线平行 ∠ADC 两直线平行,同位角相等 垂直定义 等量代换 垂直定义 13.略
14.AE∥DC
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
